机器学习算法(8)——决策树算法

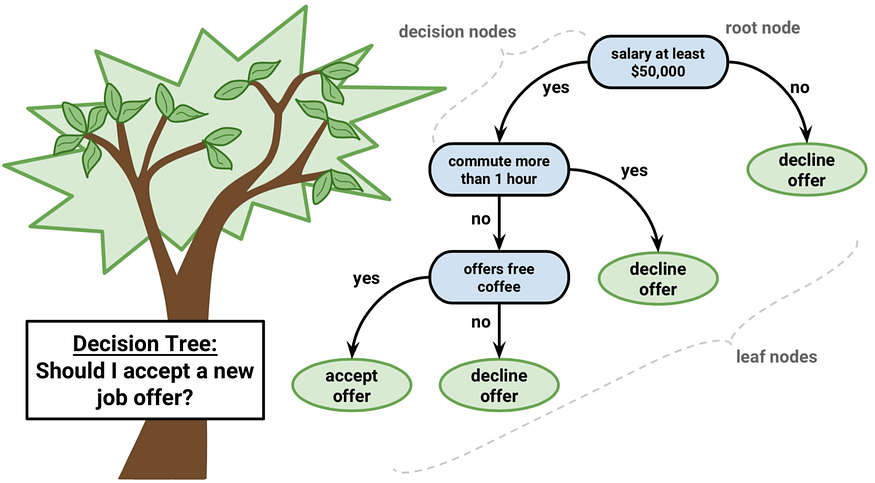
一、说明

????????在这篇文章，我将重点讨论决策树的目的。决策树是用于解决回归和分类问题的监督学习算法中最强大的算法之一。

????????我们将通过使用特定数据集的各种示例来探讨这个概念。决策树涉及编写if-else 条件，这一点很重要。

二、一个具体示例

2.1 示例1：

了解预防心脏病发作的风险

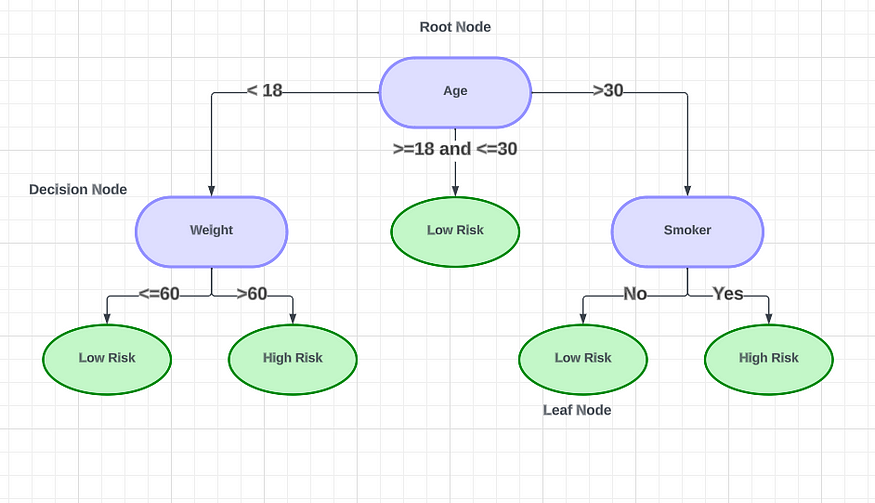
心脏病发作的决定

????????该图说明了基于某些因素的心脏病发作的概率。如果此人的年龄在18 岁以下，则会导致左侧的决策节点。在那里，我们考虑这个人的体重。如果体重低于60公斤，心脏病发作的风险较低。如果体重超过60公斤，风险就很高。对于年龄超过30岁的人，我们移动到右侧的决策节点。在那里，我们确定此人是否吸烟。不吸烟者的风险较低，而吸烟者的风险较高。对于年龄在18岁至30岁之间的人来说，心脏病发作的风险较低。末尾的绿色音符是叶节点。

????????决策树的最顶层节点称为根节点。该节点根据属性值递归地对树进行分区，这称为递归分区。由此产生的类似流程图的结构是一个极好的决策工具，因为它模仿了人类的思维。决策树是一种通过使用嵌套的 if-else 语句来解决特定问题的方法。这些树通过代表不同决策点的节点进行可视化。为了更好地理解决策树背后的数学原理，我们将一起研究示例数据集。

2.2 示例2：

????????使用决策树，我们可以确定某人是否能够打高尔夫球。

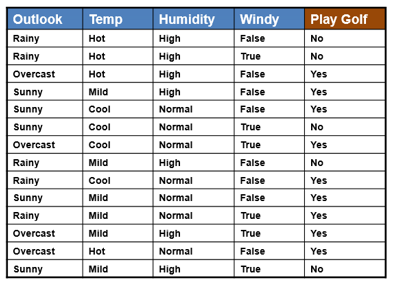
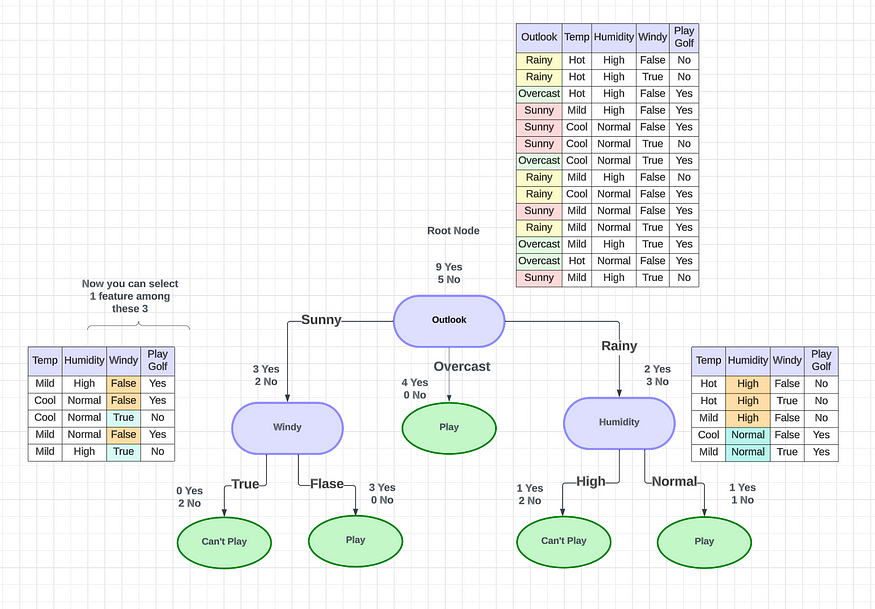
????????在这种特殊情况下，树将如何工作？首先，您可以选择任何特定的功能来绘制决策树（在选择功能之前，您可以只考虑几个事实。您将在本文的后半部分中了解它们。这里我随机选择Outlook作为功能）。

????????对于Outlook，您将能够发现有9 个“是”和 5 个“否”可以打高尔夫球。在 Outlook 功能中，我们有多少个类别？有 3 个类别：晴天、阴天和雨天。我们将尝试根据我拥有的三个类别创建三个节点。

????????对于Sunny，我们有3 个是和 2 个否。在阴天的情况下，我们有4 个是和 0 个否。对于Rainy，我们有2 个是和 3 个否。在这种情况下，有两种类型的拆分，

• 纯分体（下图中的绿色形状）
• 不纯的分裂（下图中的紫色形状）

????????阴天条件有4 个 yes 和 0 个 no。0 no表示它是纯粹的分割，因为相对于阴天，它总是变成 yes。这条路径称为纯叶节点，前景特征为阴。我们需要找到纯分裂来实现最佳决策树。

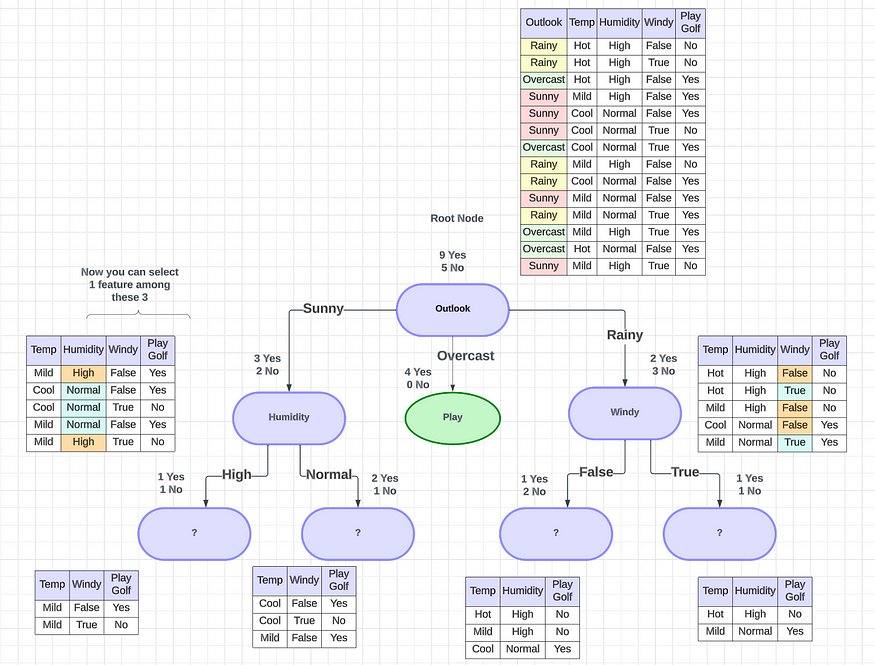
????????晴天条件有3个是和2个否，是不纯的。然后我们可以采取下一个功能。假设我们可以将下一个特征作为晴天的湿度和雨天的风。然后我们可以再次进行分割。这种分裂将会发生，直到找到一个纯节点（纯分裂）。

2.3 上图是我们能找到的最好的决策树吗？

????????没有！

????????如果 Outlook 天气晴朗，则选择“风”作为下一个功能，如果Outlook 下雨，则选择“湿度”作为下一个功能，您将获得像这样的正确决策树，其中包含纯分割和最小分割。

您可能有两个问题：我们如何识别纯分割以及如何选择特征？有几种机制可以预测这些事情。

三、我们如何计算/识别纯分裂？

????????我们使用两种不同的东西来识别纯分裂（两者都用来识别分裂的纯度），

• 熵——熵衡量节点分裂的不纯度。熵最终用于计算信息增益。下面是熵的公式，其中p(yes)是训练数据集中正类的概率，?p(No)是负类的概率。每个节点根据条件进行分裂并产生“是”或“否”。正类是属于“是”?的样本数量，负类是属于“否”的样本数量。

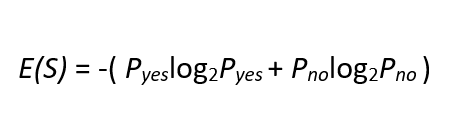
熵公式

--------------------------------------------
Entropy  = -p1 * log2(p1) -p0 * log2(p0) 
--------------------------------------------
p1 = Probabilty of Yes
p0 = Probabilty of No

Example: R1 - Root node feature
         Q1 - Category 1 Node
         Q2 - Category 2 Node

       R1(6Y,3N)
      / \
     /   \
    /     \
   Q1      Q2
(3Y,3N)    (3Y,0N)


// Based on the Q2 Category Node let's calculate the Entropy,
Entropy  = -p1 * log2(p1) -p0 * log2(p0)
p1 = Probabilty of Yes
   = 3/3
p0 = Probabilty of No
   = 0/3
Entropy  = -p1 * log2(p1) -p0 * log2(p0)
         = -3/3 * log2(3/3) - 0/3 * log2(0/3)
         = -1 log2 1 - 0
         = 0
Note : Whenever the answer of the Entropy is 0. That is a pure split node

// Based on the Q1 Category Node let's calculate the Entropy,
Entropy  = -p1 * log2(p1) -p0 * log2(p0)
p1 = Probabilty of Yes
   = 3/6 = 1/2
p0 = Probabilty of No
   = 3/6 = 1/2
Entropy  = -p1 * log2(p1) -p0 * log2(p0)
         = -1/2 * log2(1/2) - 1/2 * log2(1/2)
         = - log2(1/2)
         = 1

Note: This is not a pure split(most impure node). Here you got 50 50 possibility.

????????熵的值范围在0 到 1 之间。熵为 0 表示纯节点，1 表示最不纯的节点（其中“是”和“否”的比例为 50-50?）

????????该图显示了相对于p1和p0值而言熵可以取的值。

• 基尼不纯度——基尼不纯度是一种当目标变量是分类变量时分割节点的方法。这是分割决策树最流行和最简单的方法。

P = Probability of Yes and No
c = No of Outputs {Yes, No} =  2

Example: R1 - Root node feature
         Q1 - Category 1 Node
         Q2 - Category 2 Node

       R1(6Y,3N)
      / \
     /   \
    /     \
   Q1      Q2
(3Y,3N)    (3Y,0N)

// Based on the Q1 Category Node let's calculate the Gini Impurity,

Formula 
===========
Gini  = 1 - i =1 -> c Σ (p1)^2
      = 1 - [(Pyes)^2 + (Pno)^2]
      = 1 - [(1/2)^2 + (1/2)^2]
      = 1 - 1/2
      = 1/2 = 0.5  <--- Impure Split

Note: This is not a pure split(impure split)

????????该图显示了基尼杂质相对于p1和p0值可以取的值。基尼杂质的值范围?在0 到 0.5 之间。熵为0表示纯节点，0.5表示最不纯的节点（其中“是”和“否”的比例为 50-50?）

????????????????????????????????????????????????当我们使用熵或基尼杂质时？

????????决策树的时间复杂度最差。如果你有 100 个特征，你将通过将许多特征一一划分并计算来继续比较。标准决策树学习算法的时间复杂度为O(m·n2)。?如果你有更多的特征，熵将需要更多的时间来执行。使用基尼杂质进行大量计算也是如此。如果您有一小部分功能，那么您可以使用Entropy。

四、特征是如何选择的？

4.1 信息增益

????????信息增益是用于确定应使用哪个特征来分割决策树的每个内部节点处的数据的度量。它是使用熵计算的。

????????

????????

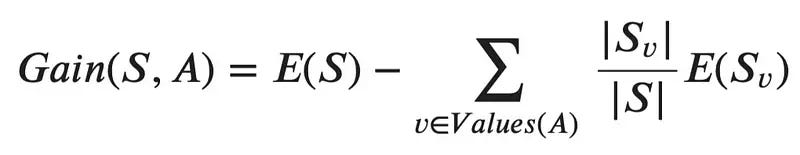
信息增益公式

// Assume I have 3 features like R1, R2, R3
I am going to draw the decision tree using 2 splitting scenarios.
// Example 1 : R1 as the root node and Q1 and the Q2 as the category nodes
// Example 2 : R2 as the root node and Q1, Q2 and Q3 as the category nodes

Example 1: R1 - Root node feature
         Q1 - Category 1 Node
         Q2 - Category 2 Node

       R1(9Y,5N)
      / \
     /   \
    /     \
   Q1      Q2
(6Y,2N)    (3Y,3N)

Step 1: First calculate the EntropyE(S) of Root Node 
Entropy of R1 root Node,
Entropy  = -p1 * log2(p1) -p0 * log2(p0)
         = - 9/14 * log2(9/14) -5/14 * log2(5/14)
         = 0.9402

Step 2: Calculate the EntropyE(Sv) of category Nodes
Entropy of Q1 Node,
Entropy  = -p1 * log2(p1) -p0 * log2(p0)
         = - 6/8 * log2(6/8) -2/8 * log2(2/8)
         = 0.8112   <---  Impure split

Entropy of Q2 Node,
Entropy  = -p1 * log2(p1) - p0 * log2(p0)
         = - 3/6 * log2(3/6) - 3/6 * log2(3/6)
         = 1   <---  Impure split

Step 3 : Get the sum of |Sv|/|S|
|Sv| = No of category Samples
|S|  = Total number of Samples


|Sv| of Q1 = 8
|Sv| of Q2 = 6
|S| = 8 + 6 = 14

Formula:
==========
Gain(S,A) = E(S) - Σ [|Sv|/|S|  E(Sv)]
Gain(S,A) = 0.94 - {[8 /14 * 0.81] + [6/14 * 1]}
          = 0.94 - {0.463 + 0.429}
          = 0.94 - 0.89
          = 0.0481


Example 2: R2 - Root node feature
         Q1 - Category 1 Node
         Q2 - Category 2 Node
         Q3 - Category 2 Node

    R2(12Y,6N)
      /  |   \
     /   |    \
    /    |     \
  Q1     Q2     Q3
(6Y,2N) (4Y,2N) (2Y,2N)

Step 1: First calculate the EntropyE(S) of Root Node 
Entropy of R1 root Node,
Entropy  = -p1 * log2(p1) -p0 * log2(p0)
         = - 12/18 * log2(12/18) -6/18 * log2(6/18)
         = 0.91829

Step 2: Calculate the EntropyE(Sv) of category Nodes
Entropy of Q1 Node,
Entropy  = -p1 * log2(p1) -p0 * log2(p0)
         = - 6/8 * log2(6/8) -2/8 * log2(2/8)
         = 0.8112   <---  Impure split

Entropy of Q2 Node,
Entropy  = -p1 * log2(p1) -p0 * log2(p0)
         = - 4/6 * log2(4/6) -2/6 * log2(2/6)
         = 0.9183   <---  Impure split


Entropy of Q3 Node,
Entropy  = -p1 * log2(p1) -p0 * log2(p0)
         = - 2/4 * log2(2/4) -2/4 * log2(2/4)
         = 1   <---  Impure split

Step 3 : Get the sum of |Sv|/|S|
|Sv| = No of category Samples
|S|  = Total number of Samples

|Sv| of Q1 = 8
|Sv| of Q2 = 4
|Sv| of Q3 = 6
|S| = 8 + 6 = 18

Formula:
==========
Gain(S,A) = E(S) - Σ [|Sv|/|S|  E(Sv)]
Gain(S,A) = 0.91829 - {[8 /18 * 0.8112] + [6/18 * 0.9183] + [4/18 * 1]}
          = 0.0294

????????现在示例 1 和 2 的信息增益值如下，
????????示例 1：
????????信息增益(R1) =?0.0481
????????示例 2：
????????信息增益(R2) =?0.0294

4.2 我应该首先使用哪个功能开始拆分？

????????这里R1 >> R2。每次你都应该追求更高的信息增益值。在此用例中，您应该使用R1 功能进行拆分。

注意：这里我计算了两条可以获得信息增益的路径。但是您应该计算所有路径的所有可能的信息增益值，并且应该识别提供最大信息增益值的要素。

五、数值变量的决策树分割

5.1 决策树如何分割数据

????????理解决策树中数值变量的无决策分割可能很棘手。处理数值变量时如何执行拆分。想象一下我们有一个带有排序值的数字特征。为了执行决策树分割，算法首先按升序对所有值进行排序。然后，它考虑阈值并创建多个树。将选择具有最高信息增益的树。

--------------------------
Feature 1    Output
--------------------------
1.5          Yes 
2            Yes
2.7          No
3            Yes
3.2          No
3.5          No
4.1          Yes
4.6          No

????????假设阈值为1.5，将根据该值检查该功能。如果小于或等于 1.5 ，将创建一个分支（左），大于 1.5 时将创建另一个分支（右）。是-否概率值是根据给定的输出特征计算的。

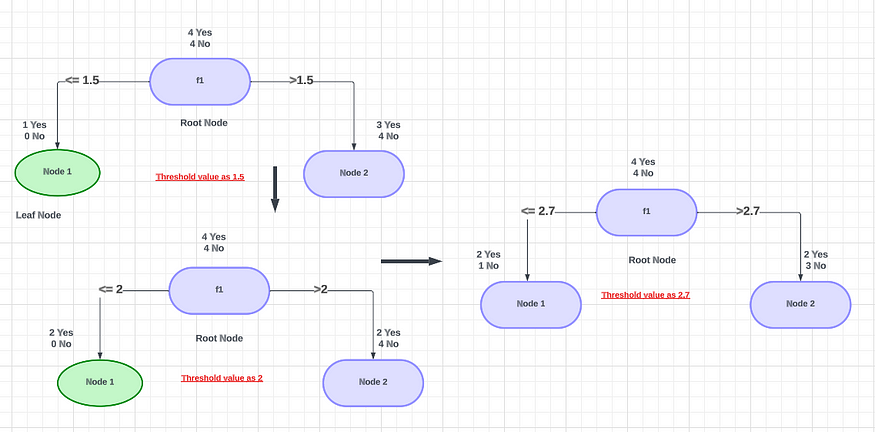
????????然后进入下一步，下一个阈值将被选择为2。然后您可以根据输出计算是/否值。之后，下一个阈值将被选择为2.7。同样，您可以计算所有组合的所有可能性。从所有组合中，选择具有最佳熵或信息增益的特征进行分割。然而，在处理数百万条记录时，此操作的时间复杂度非常高，使得决策树和集成技术的训练过程非常耗时。

5.2 如何用决策树回归

????????让我们考虑一个有 2 个变量的数据集，如下所示。我们需要构建一个回归树，在给定 X 的情况下最好地预测 Y。

// Let’s consider a dataset where we have 2 variables, as shown below. 
// we need to build a Regression tree that best predicts the Y given the X.

x      y
1      1
2      1.2
3      1.4
4      1.1
5      1
6      5.5
7      6.1
8      6.7
9      6.4
10     6
11     6
12     3
13     3.2
14     3.1

????????步骤 1?- 要将给定的数据集分为A 部分和 B 部分，第一步是对X上的数据集进行排序，这已经在此处完成。接下来，计算变量 X 中前两行的平均值为 (1+2)/2=1.5。最后，将数据集分为两部分，部分 A 和部分 B ，以值X<1.5 和 X>=1.5分隔。A 部分仅包含一个点，即第一行(1,1)，所有其他点都在B 部分中。现在，分别取 A 部分中所有 Y 值的平均值和 B 部分中所有 Y 值的平均值。这 2 个值分别是 x < 1.5 和 x ≥ 1.5 时决策树的预测输出。使用预测值和原始值计算均方误差。

????????步骤 2 —在步骤 1 中，我们计算了基于此的数据集排序 X 分割的前 2 个数字的平均值，并计算了预测。然后，我们再次执行相同的过程，但这一次，我们计算已排序的 X 的后 2 个数字的平均值( (2+3)/2 = 2.5 )。然后，我们再次根据X < 2.5 和 X ≥ 2.5 将数据集分为 A 部分和 B 部分并预测输出，找到均方误差，如步骤 1 所示。对第三个 2 个数字、第四个 2 个数字重复此过程数字，第 5 个、第 6 个、第 7 个直到第 n-1 个 2 个数字（其中 n 是数据集中的记录数或行数）。

????????步骤 3 —现在我们已经计算出n-1 均方误差，我们需要选择要分割数据集的点。该点就是在该点处分裂时产生最低均方误差的点。在这种情况下，点是x=5.5。因此，树将分为两部分。x<5.5且x≥5.5。以这种方式选择根节点，并且朝向根节点的左子节点和右子节点的数据点进一步递归地暴露于相同的算法以进一步分裂。

该算法背后的基本思想是找到自变量中的点将数据集分成两部分，以便在该点处最小化均方误差。该算法以重复的方式执行此操作并形成树状结构。我们选择这些点的方式是通过迭代过程计算所有分割的均方误差并选择mse值最小的分割。所以，这很自然。

六、 决策树剪枝

????????修剪是一种删除决策树中阻止其生长到其完整深度的部分的技术。它从树中删除的部分是不提供对实例进行分类的能力的部分。经过全面深度训练的决策树很可能会导致训练数据过度拟合，因此剪枝很重要。

????????简而言之，决策树剪枝的目的是构建一种算法，该算法在训练数据上表现较差，但在测试数据上概括得更好。调整决策树模型的超参数可以使您的模型更加公正，并为您节省大量时间和金钱。

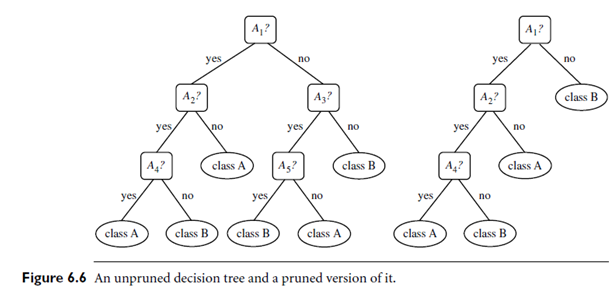
6.1 预剪枝

????????决策树的预剪枝技术是在训练管道之前调整超参数。它涉及称为“早期停止”的启发式方法，它会停止决策树的生长，从而防止其达到其完整深度。

????????它会停止建树过程，以避免产生样本较小的叶子。在树分裂的每个阶段，都会监视交叉验证错误。如果误差值不再减少——那么我们就停止决策树的生长。

????????可以调整以提前停止并防止过度拟合的超参数包括：

????????max_depth，?min_samples_leaf， 和?min_samples_split

????????这些相同的参数也可用于获得稳健的模型。但是，您应该谨慎，因为过早停止也可能导致拟合不足。

6.2 后剪枝

????????后剪枝与预剪枝相反，允许决策树模型生长到其完整深度。一旦模型增长到其最大深度，就会移除树枝以防止模型过度拟合。

????????该算法将继续将数据划分为更小的子集，直到产生的最终子集在结果变量方面相似。树的最终子集将仅包含几个数据点，允许树将数据学习到 T。但是，当引入与学习数据不同的新数据点时，可能无法很好地预测。

????????可以调整后剪枝和防止过度拟合的超参数是：ccp_alpha

??ccp代表成本复杂性修剪，可以用作控制树大小的另一个选项。较高的值ccp_alpha将导致修剪的节点数量增加。

????????成本复杂度剪枝（后剪枝）步骤：

1. 全面深度训练您的决策树模型
2. 使用计算 ccp_alphas 值cost_complexity_pruning_path()
3. 使用不同的值训练您的决策树模型ccp_alphas并计算训练和测试性能分数
4. 绘制每个值的训练和测试分数ccp_alphas。

????????该超参数还可用于调整以获得最适合的模型。

????????这就是关于决策树的全部内容，我希望您能够很好地理解这个主题。在下一篇文章中，我将讨论集成技术。