【YOLO系列】 YOLOv4之(Hard)NMS、Soft NMS、DIOU NMS（附代码）

一、NMS

????????1、简述

????????NMS (Non-Maximum Suppression，非极大值抑制)，是一种在计算机视觉领域常用的技术，用于处理基于深度学习的目标检测模型输出目标框的重叠问题。在目标检测任务中，算法通常会生成多个候选框来表示可能包含目标的区域。由于图像中的目标可能以不同的尺度和位置出现，这些候选框往往会有一定的重叠。在经典的NMS中，得分最高的检测框和其它检测框逐一计算出一个对应的IoU值，并将该值超过NMS threshold的框全部过滤掉。可以看出，在经典NMS算法中，IoU是唯一考量的因素。

????????2、步骤

????????NMS的实现步骤主要包括以下几个步骤：

????????1. 选择框和置信度：首先，选择某一类物体的所有检测框和对应的置信度，将这些框和置信度放到一个容器中。

????????2. 排序：然后，对所有检测框的置信度进行降序排序。

????????3. 选择置信度最高的框：取出当前置信度最高的框，记为proposal_max。

????????4. 计算IoU：然后，将proposal_max与容器中剩余的框逐一进行IoU（交并比）计算。IoU计算的结果反映了两个框的重叠程度。

????????5. 判断是否删除：如果某个框与proposal_max的IoU值大于设定的 threshold阈值，则将该框及其置信度从容器中删除。

????????6. 重复上述步骤：重复步骤3-5，直到容器中没有剩余的框或者proposal_max的置信度低于设定的阈值为止。

????????需要注意的是，在实现NMS时，阈值的选择是关键，阈值的选择会影响到目标检测算法的性能。通常需要通过实验来找到最优的阈值设置。

????????3、优缺点

????????（1）优点

? ? ? ? a. 提高准确率：通过抑制重叠程度较高的非最高置信度框，NMS可以有效减少冗余框，从而提高目标检测的准确率。

? ? ? ? b. 简化后续处理：重叠框问题会给后续处理带来困难，如物体跟踪和识别。NMS能够提供清晰、无重叠的框，简化后续处理流程。

????????（2）缺点

? ? ? ? a. 计算效率低：NMS需要进行排序和比较操作，时间复杂度较高，计算效率相对较低。对于大规模数据集，处理速度可能会成为瓶颈。

? ? ? ? b. 对小物体检测效果不佳：由于小物体的检测框相对较少，且容易与大物体发生重叠，导致NMS处理后可能会漏检一些小物体。

? ? ? ? c. 依赖阈值选择：NMS的效果高度依赖于阈值的选择。如果阈值设置不当，可能会导致误检或漏检的情况。

? ? ? ? d. 无法处理高密度目标的情况：当场景中存在大量密集分布的目标时，NMS处理的效果可能会受到限制。

? ? ? ? e. 未考虑框的置信度变化：NMS仅根据框的IoU值进行判断，未考虑框的置信度变化，可能会影响到算法的准确性。

????????4、代码实现

def nms(boxes, scores, threshold):
    """
    非极大值抑制函数
    :param boxes: 候选框的坐标，以左上角和右下角的形式表示，形状为(num_boxes, 4)
    :param scores: 候选框的得分，形状为(num_boxes,)
    :param threshold: NMS阈值
    :return: 经过非极大值抑制后的框的索引
    """
    x1 = boxes[:, 0]
    y1 = boxes[:, 1]
    x2 = boxes[:, 2]
    y2 = boxes[:, 3]
    areas = (x2 - x1 + 1) * (y2 - y1 + 1)
    # 将scores按照降序排序，返回是scores的索引值
    order = scores.argsort()[::-1]
    keep = []
    while order.size > 0:
        i = order[0]
        keep.append(i)
        xx1 = np.maximum(x1[i], x1[order[1:]])
        yy1 = np.maximum(y1[i], y1[order[1:]])
        xx2 = np.minimum(x2[i], x2[order[1:]])
        yy2 = np.minimum(y2[i], y2[order[1:]])
        w = np.maximum(0, xx2 - xx1 + 1)
        h = np.maximum(0, yy2 - yy1 + 1)
        inter = w * h
        iou = inter / (areas[i] + areas[order[1:]] - inter)
        idx = np.where(iou <= threshold)[0]
        order = order[idx + 1]
    return keep

????????NMS在计算机视觉领域得到了广泛的应用，例如边缘检测、人脸检测、目标检测等。使用NMS的原因在于以目标检测为例，目标检测的过程中在同一目标的位置上会产生大量的候选框，这些候选框相互之间可能会有重叠，此时我们需要利用NMS找到最佳的目标边界框，消除冗余的边界框。

---

二、Soft NMS

????????论文下载：Improving Object Detection With One Line of Code

????????1、NMS存在的问题

????????非极大值抑制是目标检测的重要组成部分。首先，它根据检测框的得分对它们进行分类。选择得分最高的检测框M，并抑制与M有显著重叠(使用预定义阈值)的所有其他检测框。此过程递归地应用于剩余的框。根据算法的设计，如果一个对象位于预定义的重叠阈值内，则会导致miss。

????????如上图中所示，两匹马的检测结果分别为0.8（绿色框）和0.95（红色框），但是如果按照传统NMS进行处理，首先选中检测得分最高的红色框，然后绿色框会因为与之重叠面积大于阈值而被删掉，这就导致了漏检。

????????另外，如果降低threshold值，就会出现大量检测框被误删，如果升高threshold值，则会导致出现大量的错检框或者重复框。

????????针对上述问题，作者提出了一种Soft NMS方法，只需改动一行代码即可有效改进传统的NMS算法。

????????2、Soft NMS简述

????????针对NMS的问题，作者对传统的贪婪NMS算法提出了一种单行修改，即将检测分数作为重叠的增加函数来降低，而不是像NMS那样将分数设置为零。直观地说，如果一个边界框与M有非常高的重叠，就应该给它一个非常低的分数，如果重叠很低，则可以保持原来的检测分数。由于Soft-NMS不需要任何额外的训练，并且易于实现，因此可以很容易地集成到目标检测中。

????????3、步骤

????????Soft NMS算法的中心思想：拒绝粗鲁的删除所有IOU大于threshold的框，而是采用降低其置信度来实现。

????????在文中，作者采用了一个线性函数作为衰减函数，当与M有更高重叠的检测框的分数时，应该衰减得更多，因为它们有更高的假阳性可能性，而远离M的候选框则不会受到影响。

????????然而，就重叠而言，它不是连续的，当达到NMS阈值时，会突然施加惩罚。而如果惩罚函数是连续的，那将是理想的，否则它可能导致检测排序列表的突然变化。一个连续的惩罚函数在两个候选框没有重叠时应该没有惩罚，在高重叠时应该有很高的惩罚。同样，当重叠度很低时，应该是逐渐增加惩罚，因为M不应该影响与它重叠度很低的候选框的分数。然而，当候选框bi与M的重叠接近于1时，bi应该被严重扣分。考虑到这一点，作者建议用高斯惩罚函数来更新剪枝步骤：

????????其实Soft NMS的计算步骤与NMS类似，Soft NMS的计算复杂度与传统的NMS相同，都是O(N2)。

????????4、优缺点

????????（1）优点

????????a. 提高了目标检测的准确率，特别是在处理重叠框问题时。

????????b. 算法复杂度与传统的NMS相同，但比NMS更加灵活，能够更有效地处理框之间的重叠问题。

????????c. 易于集成到任何物体检测流程中，不需要重新训练原有的模型。

????????d. 仅需要增加一个超参数sigma，阈值nms本来也有，iou是算出来的。

????????e. 在标准数据集上表现提升，例如PASCAL - VOC2007和MS-COCO。

????????（2）缺点

????????a. 无法处理高密度目标的情况：当场景中存在大量密集分布的目标时，Soft NMS处理的效果可能会受到限制。

????????b. 计算效率相对较低：Soft NMS需要进行排序和比较操作，时间复杂度较高，计算效率相对较低。在大规模数据集上，Soft NMS可能会成为性能瓶颈。

????????5、代码实现

def soft_nms(boxes, scores, sigma=0.5, Nt=0.5, threshold=0.5, method=2):
    """
    soft nms
    :param boxes: 候选框的坐标，以左上角和右下角的形式表示，形状为(num_boxes, 4)
    :param scores: 候选框的得分，形状为(num_boxes,)
    :param sigma:
    :param Nt:
    :param threshold:
    :param method: method == 1: linear; 2:  gaussian; other: original NMS
    :return:
    """
    N = boxes.shape[0]
    pos = 0
    maxscore = 0
    maxpos = 0

    for i in range(N):
        maxscore = scores[i]
        maxpos = i
        # 获取第i个框的坐标值与分数
        tx1 = boxes[i, 0]
        ty1 = boxes[i, 1]
        tx2 = boxes[i, 2]
        ty2 = boxes[i, 3]
        ts = scores[i]

        pos = i + 1
        # 获取最大的分数与框的索引
        while pos < N:
            if maxscore < scores[pos]:
                maxscore = scores[pos]
                maxpos = pos
            pos = pos + 1

        # 将最大值的框与对比框交换位置
        boxes[i, 0] = boxes[maxpos, 0]
        boxes[i, 1] = boxes[maxpos, 1]
        boxes[i, 2] = boxes[maxpos, 2]
        boxes[i, 3] = boxes[maxpos, 3]
        scores[i] = scores[maxpos]

        boxes[maxpos, 0] = tx1
        boxes[maxpos, 1] = ty1
        boxes[maxpos, 2] = tx2
        boxes[maxpos, 3] = ty2
        scores[maxpos] = ts

        # 最大框的坐标值
        tx1 = boxes[i, 0]
        ty1 = boxes[i, 1]
        tx2 = boxes[i, 2]
        ty2 = boxes[i, 3]
        ts = scores[i]

        pos = i + 1
        # NMS iterations, note that N changes if detection boxes fall below threshold
        while pos < N:
            x1 = boxes[pos, 0]
            y1 = boxes[pos, 1]
            x2 = boxes[pos, 2]
            y2 = boxes[pos, 3]
            s = scores[pos]

            area = (x2 - x1 + 1) * (y2 - y1 + 1)
            iw = (min(tx2, x2) - max(tx1, x1) + 1)
            if iw > 0:
                ih = (min(ty2, y2) - max(ty1, y1) + 1)
                if ih > 0:
                    # 求最大分数的框与第i个框的iou
                    ua = float((tx2 - tx1 + 1) * (ty2 - ty1 + 1) + area - iw * ih)
                    iou = iw * ih / ua

                    if method == 1:  # linear
                        if iou > Nt:
                            weight = 1 - iou
                        else:
                            weight = 1
                    elif method == 2:  # gaussian
                        weight = np.exp(-(iou * iou) / sigma)
                    else:  # original NMS
                        if iou > Nt:
                            weight = 0
                        else:
                            weight = 1

                    scores[pos] = weight * s
                    print(scores)

                    # 如果框得分低于阈值，则通过交换最后一个框来丢弃该框
                    # update N
                    if scores[pos] < threshold:
                        boxes[pos, 0] = boxes[N - 1, 0]
                        boxes[pos, 1] = boxes[N - 1, 1]
                        boxes[pos, 2] = boxes[N - 1, 2]
                        boxes[pos, 3] = boxes[N - 1, 3]
                        scores[pos] = scores[N - 1]
                        N = N - 1
                        pos = pos - 1

            pos = pos + 1
    keep = [i for i in range(N)]
    return keep

---

三、DIOU NMS

论文下载：Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression

????????1、简述

????????DIOU NMS是一个改进的NMS算法，它不仅考虑了两个框的IoU（交并比）值，还考虑了两个框的中心点之间的距离，以决定是否保留一个框。

????????DIOU具体内容详见：【YOLO系列】 Smooth L1 Loss、IOU、GIOU、DIOU、CIOU（附代码实现）

????????2、步骤

????????DIOU NMS与NMS实现的步骤相同，只是把IOU的计算换成了DIOU计算

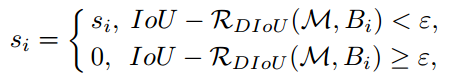
????????3、代码实现

def Diou_nms(boxes, scores, threshold=0.3):
    """
    非极大值抑制函数
    :param boxes: 候选框的坐标，以左上角和右下角的形式表示，形状为(num_boxes, 4)
    :param scores: 候选框的得分，形状为(num_boxes,)
    :param threshold: NMS阈值
    :return: 经过非极大值抑制后的框的索引
    """
    x1 = boxes[:, 0]
    y1 = boxes[:, 1]
    x2 = boxes[:, 2]
    y2 = boxes[:, 3]
    areas = (x2 - x1 + 1) * (y2 - y1 + 1)

    b1_w = x2 - x1
    b1_h = y2 - y1
    center_x1 = x1 + b1_w / 2
    center_y1 = y1 + b1_h / 2

    # 将scores按照降序排序，返回是scores的索引值
    order = scores.argsort()[::-1]
    keep = []
    while order.size > 0:
        i = order[0]
        keep.append(i)
        xx1 = np.maximum(x1[i], x1[order[1:]])
        yy1 = np.maximum(y1[i], y1[order[1:]])
        xx2 = np.minimum(x2[i], x2[order[1:]])
        yy2 = np.minimum(y2[i], y2[order[1:]])
        w = np.maximum(0, xx2 - xx1 + 1)
        h = np.maximum(0, yy2 - yy1 + 1)
        inter = w * h
        iou = inter / (areas[i] + areas[order[1:]] - inter)

        out_max_x = np.maximum(x2[i], x2[order[1:]])
        out_max_y = np.maximum(y2[i], y2[order[1:]])
        out_min_x = np.minimum(x1[i], x1[order[1:]])
        out_min_y = np.minimum(y1[i], y1[order[1:]])

        inter_diag = (center_x1[i] - center_x1[order[1:]]) ** 2 + (center_y1[i] - center_y1[order[1:]]) ** 2
        outer_x = np.maximum((out_max_x - out_min_x), 0)
        outer_y = np.maximum((out_max_y - out_min_y), 0)
        outer_diag = (outer_x ** 2) + (outer_y ** 2)

        diou = iou - inter_diag / outer_diag

        idx = np.where(diou <= threshold)[0]
        order = order[idx + 1]
    return keep