【NeRF】体渲染

借用了 参考文章1的图片，侵删。
关于体渲染的知识，主要借鉴 参考文章1

体渲染是NeRF的核心内容，想要读懂NeRF，就要明白体渲染的基本原理。

体渲染 (Volume Rendering)

体渲染属于整个渲染技术的分支，它的目的主要是为了解决云、烟、果冻这类非刚性物体的渲染建模，可以简单理解为是为了处理密度较小的非固体的渲染。当然进一步推广到固体的渲染也说的通，NeRF 就是这样做的。

为了建模这种非刚性物体的渲染，体渲染把气体等物质抽象成一团飘忽不定的粒子群。光线在穿过这类物体时，其实就是光子在跟粒子发生碰撞的过程。

下图是体渲染建模的示意图。光沿直线方向穿过一堆粒子 (粉色部分)，如果能计算出每根光线从最开始发射，到最终打到成像平面上的辐射强度，我们就可以渲染出投影图像。而体渲染要做的，就是对这个过程进行建模。为了简化计算，我们就假设光子只跟它附近的粒子发生作用，这个范围就是图中圆柱体大小的区间。

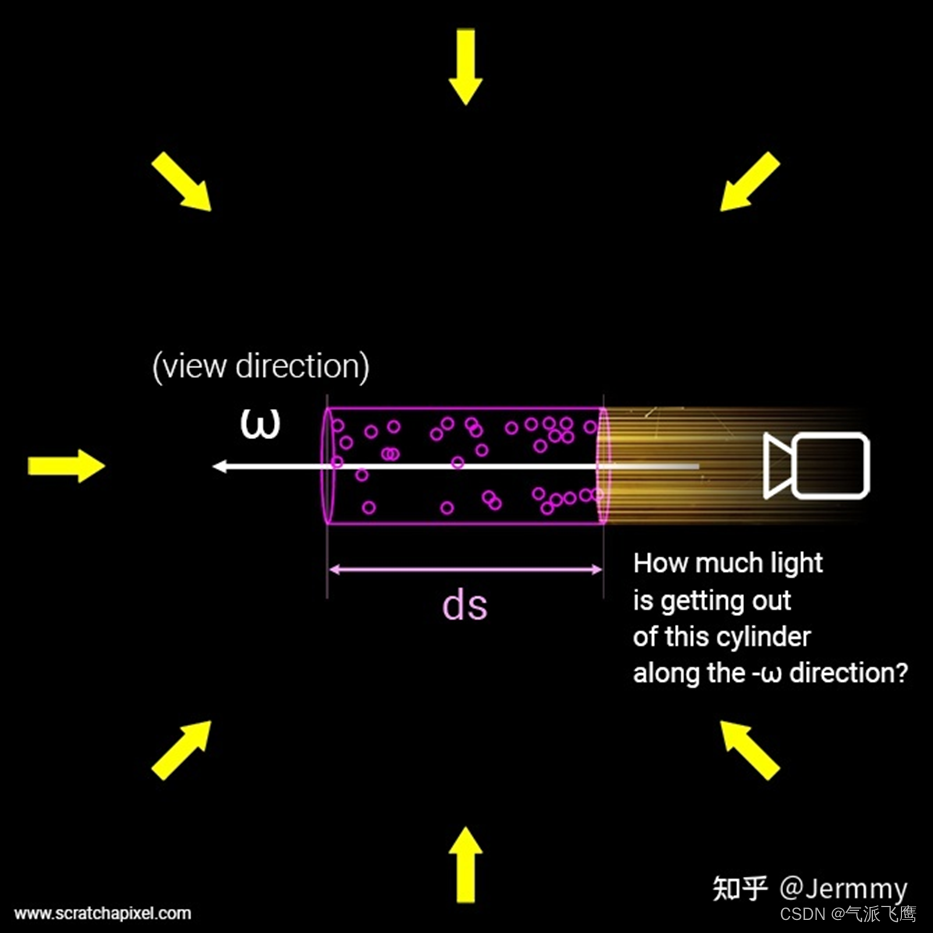
体渲染把光子与粒子发生作用的过程，进一步细化为四种类型：

• 吸收 (absorption)：光子被粒子吸收，会导致入射光的辐射强度减弱；
• 放射 (emission)：粒子本身可能发光，这会进一步增大辐射强度；
• 外散射 (out-scattering)：光子在撞击到粒子后，可能会发生弹射，导致方向发生偏移，会减弱入射光强度；
• 内散射 (in-scattering)：其他方向的光子在撞到粒子后，可能和当前方向上的光子重合，从而增强当前光路上的辐射强度。

下图是这四种情况的示意图，$L_i$表示入射光，$L_o$表示出射光。

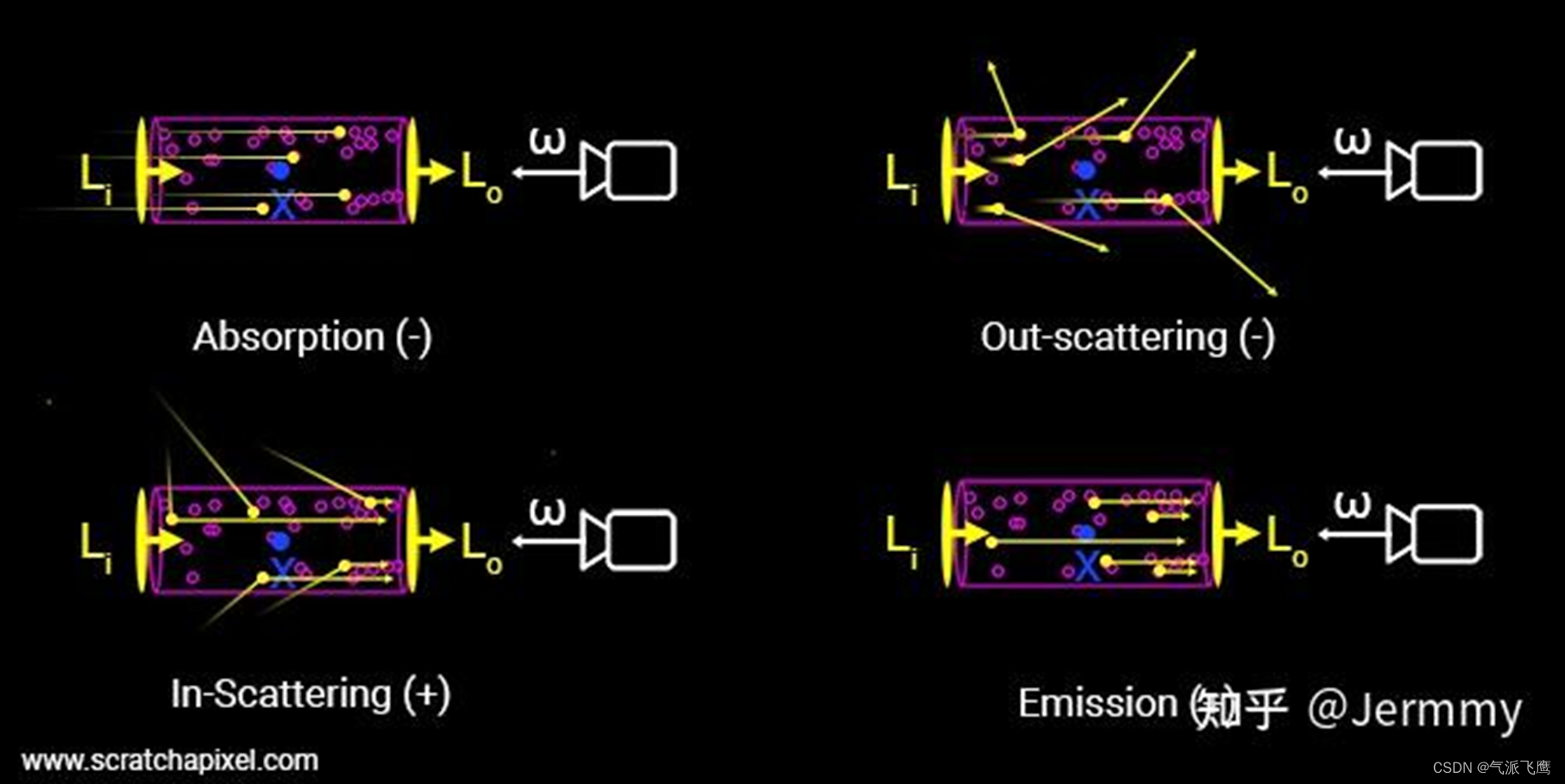
出射光与入射光之间的变化量，可以表示为这四个过程的叠加：
$L_o?L_i=dL(x,w)=emissiom+inscattering?outscattering?absorption$

其中 $x$ 表示光线上某个位置点，$w$ 表示光线发射方向。

吸收 (absorbing)

我们先剖析下吸收的过程。

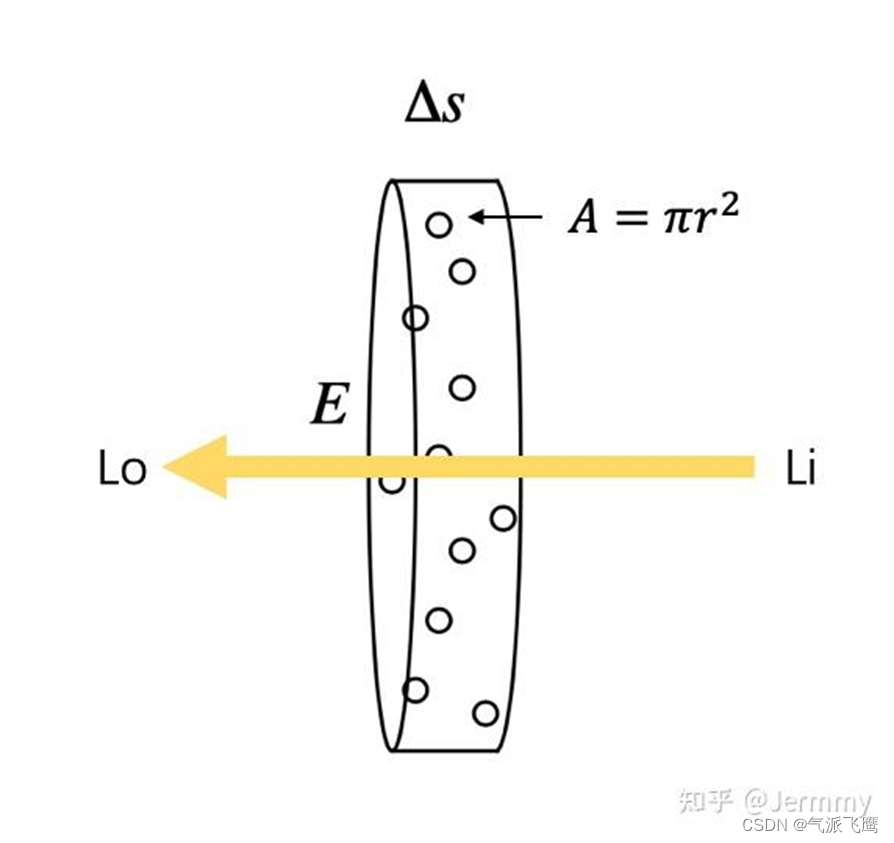
假设粒子都是半径为 $r$ 的球体，那么每个粒子的投影面积是 $A=\pi r^2$
(也就是每个粒子对光线的遮挡面积)。

假设圆柱体中粒子的密度是 $\rho$，圆柱体的底面积是 $E$。

当圆柱体足够薄 (薄到跟粒子一样厚) 的时候，可以认为粒子之间不会互相重叠 (也就是粒子都平铺在圆柱体一个横截面上)。

假定这个厚度是 $\Delta s$，那么在这个厚度内，圆柱体体积为 $E\Delta s$，粒子总数为 $\rho E\Delta s$。这些粒子遮挡的面积为 $\rho E\Delta sA$，占整个底面积的比例为 $\rho E\Delta sA/E=\rho A\Delta s$。也就是说，当一束光通过这个圆柱体的时候，有 $\rho A\Delta s$ 的概率会被遮挡。

换句话说，如果我们在圆柱体的一端发射无数光线 (假设都朝相同的方向)，在另一端接收，会发现有些光线安然通过，有些则被粒子遮挡 (吸收)。但可以确定的是，这些接受到的光线总强度，相比入射光线总强度而言，会有 $\rho A\Delta s$ 比例的衰减，即出射光的强度均值是入射光的 $\rho A\Delta s$ 倍。

数学上可以表示为：
$$I_o?I_i=?\rho (s)AI(s)\Delta s\text{\hspace{1em}(1)}$$

注意粒子密度 $\rho$ 是一个关于 $s$ 的函数，因为每个区域的密度都是不同的。另外，在后面的公式中，可能出现 $dI,\Delta I$ 轮流使用的情况，它们都是一个意思，$d$ 和 $\Delta$ 都表示一个微小的变化量。

(1) 式可以转换为常微分方程：
$$\frac{dI}{ds}=?\rho (s)AI(s)=?{\tau }_a(s)I(s)\text{\hspace{1em}(2)}$$
解方程得到
$$I(s)=I_{0}exp(?{\int }_0^s{\tau }_a(t)dt)\text{\hspace{1em}(3)}$$

公式里面的 $I_0$ (注意区分 $I_o$) 是常微分方程中的常数项，物理意义上表示光线的起始点，比如对 $I_o$ 来说，就应该表示成 $I(o)=I_{i}exp(?{\int }_i^o{\tau }_a(t)dt)$。

公式 (3) 有丰富的物理意义。

如果介质 (粒子群) 是均匀的，即 ${\tau }_a(t)$ 处处相等，那么入射光在经过介质 (粒子群) 后，辐射强度会呈指数衰减。这被称为比尔-朗伯吸收定律 (Beer-Lambert law)：

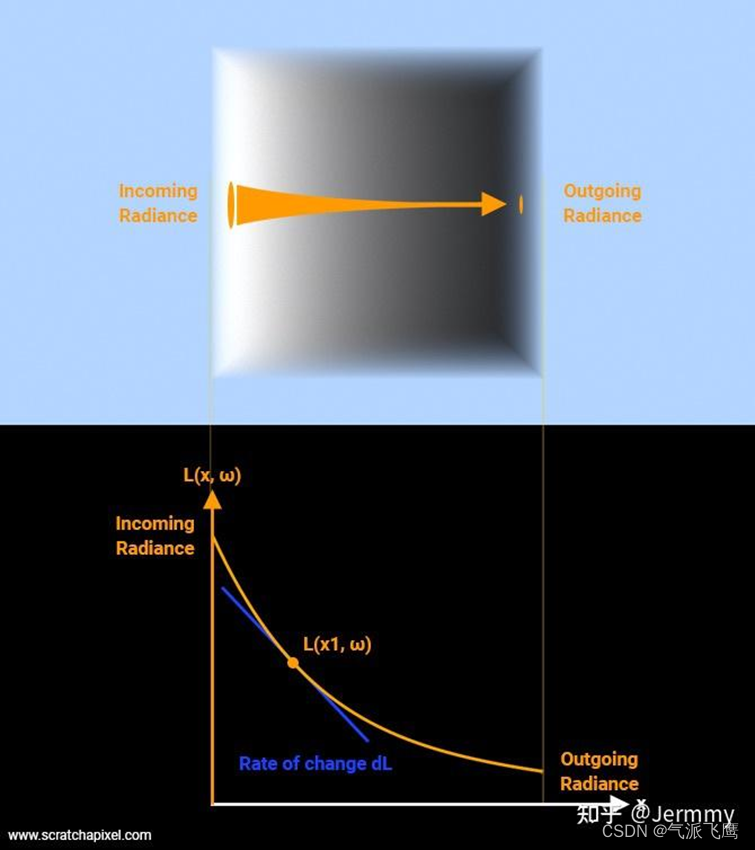
我们可以由此定义透射比 (transmittance)：
$$T(s)=\frac{I_o}{I_i}=exp(?{\int }_i^o{\tau }_a(t)dt)\text{\hspace{1em}(4)}$$
它表示粒子群某一点的透明度，数值越大，说明粒子群越透明，光线衰减的幅度就越小。

而透明度本身是关于 ${\tau }_a(t)$ 的方程，${\tau }_a(t)$ 越大，$T(s)$ 就越小。由公式 (2) 可以知道，${\tau }_a(t)=\rho (t)A$，它是由粒子密度和投影面积决定的。这在直觉上也很好理解，如果粒子密度大，粒子本身也比较大，那么遮住光线的概率也会相应提升，自然透明度也就下降了。

${\tau }_a(t)$ 也被称为光学厚度 (optical depth)。

放射 (emission)

除了吸收之外，粒子本身也可能发光。

假设单个粒子发射一束光的辐射强度为 $I_e$，那么按照前文的描述，在圆柱体足够薄的情况下，粒子总数是 $\rho AE\Delta s$，则总的发光强度为 $I_e\rho AE\Delta s$
。

如果我们在圆柱体一端去接收粒子们放射的光线，会发现有时候能接收到，有时候刚好接收点所在的光路上没有粒子，就接收不到。能接收到光线的概率为 $\rho AE\Delta s/E=\rho A\Delta s$，那么接收到的光线的平均强度为 $I_e\rho A\Delta s$。

同样地，可以得到放射光强的常微分方程：
$$\frac{dI}{ds}=I_e(s)\rho (s)A=I_e(s){\tau }_a(s)\text{\hspace{1em}(5)}$$

注意，$I_e$ 是一个关于 $s$ 的函数，因为圆柱体不同位置的粒子，所放射的光强都是有差异的。这里我们也看到，类似吸收，粒子放射的光强同样和 ${\tau }_a(s)$ 有关，这在直觉上也是合理的，如果粒子能发光，那粒子密度和粒子颗粒越大，放射的辐射均值也就越大。

这个函数的求解我们放到最后再来看。

外散射 (out-scattering)

粒子除了吸收光子，也可能会弹射光子，这个过程称为外散射，即光子被弹射出原本的光路，导致光线强度减弱。

同吸收一样，外散射对光线的「削弱」程度，也跟光学厚度相关，不过过程相对吸收来说又复杂一些，因此我们用 ${\tau }_s$ 来表示外散射对光线的削弱比例，以区别于 ${\tau }_a$。

同样地，这一过程可以表示为：
$$\frac{dI}{ds}=?{\tau }_s(s)I(s)\text{\hspace{1em}(6)}$$

内散射 (in-scattering)

光子可以被弹射走，自然就有其他光路的光子被弹射到当前光路，这一过程就是内散射。

内散射的过程比外散射又更加复杂，因为弹射到当前光路的光子可能来自多条不同的光路，因此需要综合考虑其他光路的辐射强度以及各种弹射角度。

不过本文不打算深入探究这一点，我们就认为其他光路的辐射强度为 $I(s)$，而弹射到当前光路的能量损失比为 ${\tau }_s$ (注意这里和外散射使用的是相同的系数，既然都是散射，那有些性质上自然是共通的)。

内散射的过程可以表示为：
$$\frac{dI}{ds}={\tau }_s(s)I_s(s)\text{\hspace{1em}(7)}$$

当然啦，真实的渲染过程要复杂得多，而 NeRF 利用神经网络优秀的建模能力，对部分渲染过程做了简化。因此，NeRF 使用的体渲染与传统的体渲染会有些许差异。

体渲染方程

我们把以上四个过程都综合到一个公式中：
$$\frac{dI}{ds}=?{\tau }_a(s)I(s)?{\tau }_s(s)I(s)+{\tau }_a(s)I_e(s)+{\tau }_s(s)I_s(s)\text{\hspace{1em}(8)}$$

其中，吸收和外散射都会削弱光线的辐射强度，并且由于它们都和入射光有关，因此它们共同构成了体渲染中的衰减项 (attenuation item)，而粒子发光和内散射都来自独立的光源，因此被称为源项 (source item)。

（参考文章1里面，这里对公式进行了一些变形和简化，奈何本人水平有限，看不懂原博客的结果是怎么得到的，我这里就直接对原公式进行求解，得到了下面的这个非非非非常长的公式。）
$$I(s)=exp(?{\int }_0^s{\tau }_a(s)+{\tau }_s(s)ds)({\int }_0^{s}exp({\int }_0^s{\tau }_a(s)+{\tau }_s(s)ds)({\tau }_a(s)I_e(s)+{\tau }_s(s)I_s(s))ds+C)\text{\hspace{1em}(9)}$$

这里的C就是$I_0$也就是入射光最开始的强度，在 NeRF 中把它当作是背景光。
这个公式告诉我们，出射光的强度主要由入射光 (背景光) 和源项 (粒子发光以及内散射) 等构成的，而这两者在传递过程中都伴随着相同的衰减 (${\tau }_a+{\tau }_s$)。同时由于从 $I_0$ 到 $I_s$ 的整个光路上，处处都可能存在粒子发光和内散射现象，因此源项是需要从 0 开始相加一直到 s 的，对应到公式中就是积分 ${\int }_0^s$。

有了这个公式，我们就可以建模出每一条光线在传播介质中，辐射强度的变化，并最终渲染出图像 (当然前提要知道介质中每一点的 ${\tau }_a+{\tau }_s$、$I_e$ 等信息)。

注意，虽然我们在讨论这个模型的时候一直是用辐射强度这个概念，可以直接将辐射强度$I(s)$理解成颜色。

传统的体渲染就简单介绍到这里，接下来介绍一下NeRF中的体渲染计算公式。

NeRF中的体渲染

这里主要参考文献2。

NeRF体渲染方程

思路跟传统的体渲染方法是一样的，还进行了简化，在NeRF中不考虑内散射和外散射的情况，一些数学符号的定义可能发生改变，会对变量的定义进行声明。

$r(o,d)$定义了一条光线,$o$是光源位置，$d$是表示光线方向的单位向量。对于光线上的任一位置可以用$o+td$表示。

$c(t)$表示$t$位置的粒子颜色

$\sigma (t)$是光线上$t$位置处的粒子密度，同时也表示光线在t位置行进无穷小距离时撞击粒子的可能性。

$T(t)$透射率，可以理解为光线从起点传播到$t$位置而不撞击任何粒子的概率，$T(t)?\sigma (t)$表示光线精确停止在t位置的概率。

将$T(a\to b)$定义为射线沿着射线从距离 a 传播到 b 且没有撞击粒子的概率，这与前面的$T(t)=T(0\to t)$相似。
$$T(a\to b)\equiv \frac{T(b)}{T(a)}=exp(?{\int }_a^b\sigma (t)dt)\text{\hspace{1em}(1)}$$
这个公式和体渲染（volume rendering） 中的公式3类似，但是这里使用的是密度，和前面的光学厚度(${\tau }_a=\rho (s)A$)不太一样，因为这里是一个光线上的撞击概率，直接用密度表示，而光学厚度是认为是一个圆柱上的碰撞概率所以用的密度乘圆柱底面积。

现在可以得到光线从 t=0 传播到 D 时粒子发出的光的预期值，并将其合成在背景颜色$c_{bg}$之上，即可得到NeRF中的体渲染方程。
$$C={\int }_0^{D}T(t)?\rho (t)?c(t)dt+T(D)?c_{bg}\text{\hspace{1em}(2)}$$

但是这个公式在计算机中是无法计算的，还需要对其进行离散化，将整个光路划分为n个等间距的区间，只要能算出每个区间内的颜色值，最后把 n个区间的颜色加起来，就可以得到最终的颜色了。

NeRF体渲染方程计算

对于透射率T，可以拆分为两段的乘积。

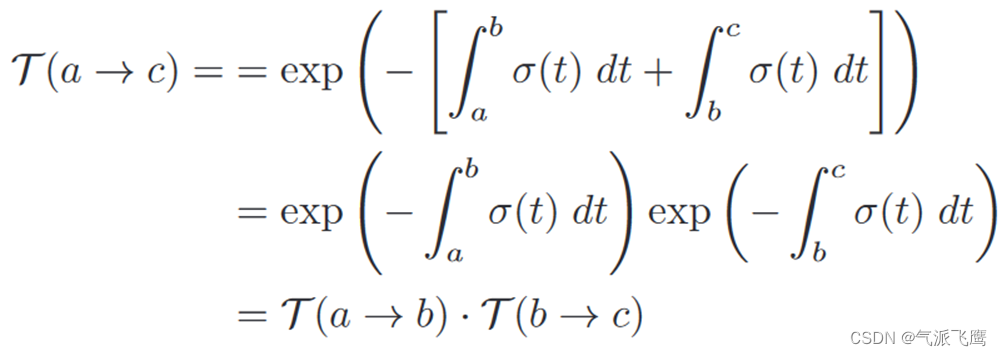
对于给定的间隔$[t_n,t_{n+1}{]}_{n=1}^N$，假设第 n 段内密度${\sigma }_n$恒定，且$t1=0$且${\delta }_n=t_{n+1}?t_n$，那么到$t_n$位置的透射率等于前n-1个区间的透射率的累乘：

对于区间[a,b]，假设区间内的粒子密度和颜色是恒定的${\sigma }_a,c_a$，那么$C(a\to b)$的计算结果如下。

结合前面的公式，将每个区间得到的颜色值进行累和即可得到离散化后的体渲染公式：

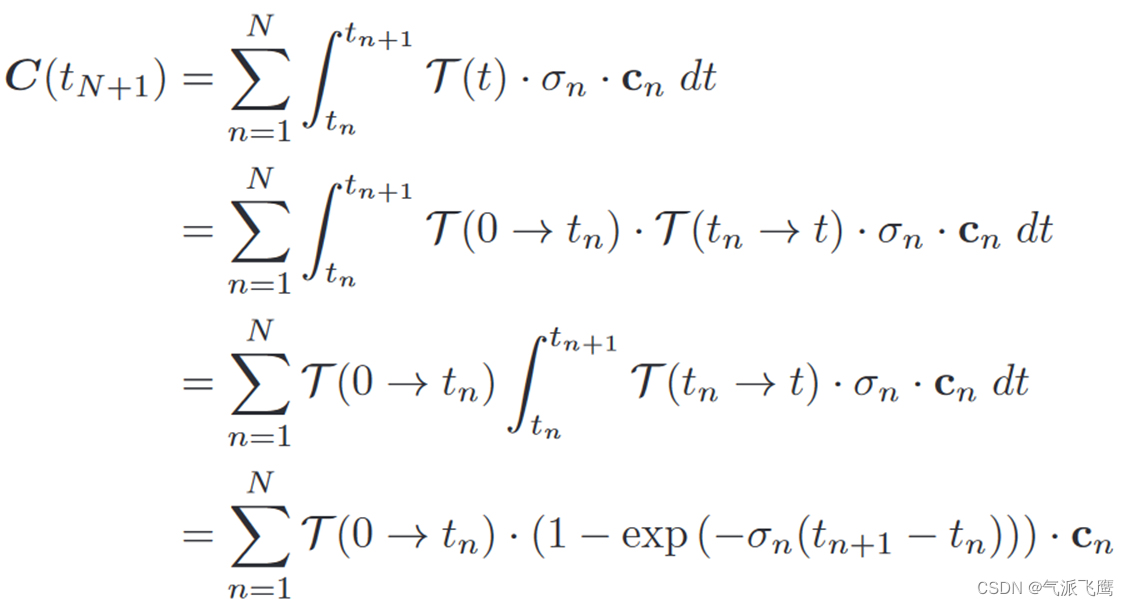
再根据前面${\delta }_n=t_{n+1}?t_n$就得到了NeRF中的体渲染公式

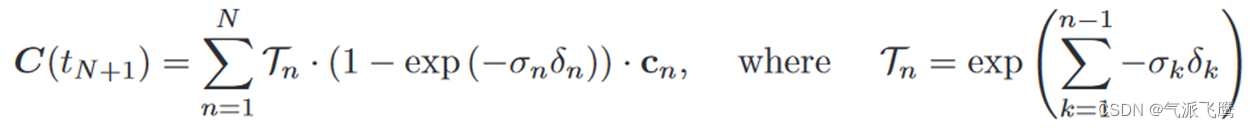
参考

1.NeRF入门之体渲染 (Volume Rendering)
2.Volume Rendering Digest (for NeRF)

主要参考文献1，文章写的很好，但是到后面讲NeRF中的体渲染公式部分，我有一些怀疑它的准确性。我自己又看了一下文献2这篇技术论文，才搞懂了NeRF中的体渲染。