RL | 强化学习算法DDPG的理论理解及代码

深度确定性策略梯度（Deep Deterministic Policy Gradient, DDPG）是一种强化学习算法，主要用于解决连续动作空间的问题。

1.理论理解

1.1.背景

在强化学习中，有两种主要类型的算法，一种是值函数（Value Function）型的，另一种是策略函数（Policy Function）型的。DDPG属于策略函数型的算法，适用于需要连续动作的环境，比如机器人控制、自动驾驶等。

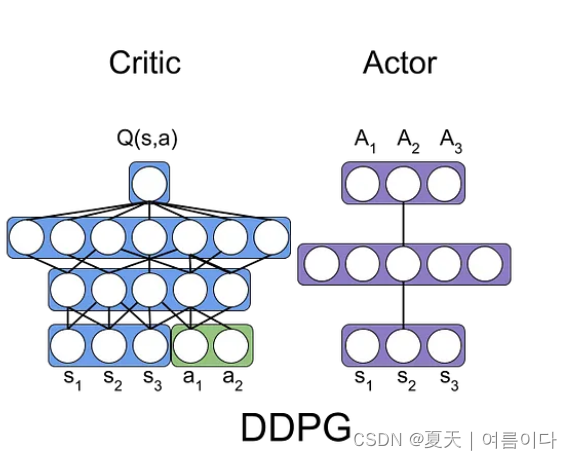
1.2.Actor-Critic 结构

DDPG使用了Actor-Critic结构，其中：

• Actor（演员）： 负责学习和输出策略，即动作的选择。
• Critic（评论家）： 负责评估 Actor 的策略，指导 Actor 更新策略。

?

1.3.确定性策略

在传统的策略梯度方法中，策略是一个概率分布，而DDPG使用的是确定性策略。这意味着给定相同的状态，策略网络输出的动作是确定的，而不是一个概率分布。

经验回放（Experience Replay）：

DDPG引入了经验回放，这是一种从先前的经验中学习的方法。它将Agent在环境中的经验存储在一个回放缓冲区中，然后从中随机抽样进行训练。这有助于打破数据之间的相关性，提高训练的稳定性。

1.4.目标网络（Target Networks）

DDPG使用两组网络，每组有一个 Actor 网络和一个 Critic 网络。这两组网络分别是当前网络和目标网络。目标网络的参数是由当前网络的参数进行软更新得到的。这有助于提高算法的稳定性，防止训练过程中的剧烈波动。

1.5.奖励信号和目标函数

DDPG的目标是最大化累积奖励。通过更新 Actor 和 Critic 的参数，算法试图找到最优的确定性策略，使得 Agent 在环境中获得最大的累积奖励。

2.代码

import torch
import torch.autograd
import torch.optim as optim
import torch.nn as nn
from model import *
from utils import *

class DDPGagent:
    def __init__(self, env, hidden_size=256, actor_learning_rate=1e-4, critic_learning_rate=1e-3, gamma=0.99, tau=1e-2, max_memory_size=50000):
        # Params
        self.num_states = env.observation_space.shape[0]
        self.num_actions = env.action_space.shape[0]
        self.gamma = gamma
        self.tau = tau

        # Networks
        self.actor = Actor(self.num_states, hidden_size, self.num_actions)
        self.actor_target = Actor(self.num_states, hidden_size, self.num_actions)
        self.critic = Critic(self.num_states + self.num_actions, hidden_size, self.num_actions)
        self.critic_target = Critic(self.num_states + self.num_actions, hidden_size, self.num_actions)

        for target_param, param in zip(self.actor_target.parameters(), self.actor.parameters()):
            target_param.data.copy_(param.data)

        for target_param, param in zip(self.critic_target.parameters(), self.critic.parameters()):
            target_param.data.copy_(param.data)
        
        # Training
        self.memory = Memory(max_memory_size)        
        self.critic_criterion  = nn.MSELoss()
        self.actor_optimizer  = optim.Adam(self.actor.parameters(), lr=actor_learning_rate)
        self.critic_optimizer = optim.Adam(self.critic.parameters(), lr=critic_learning_rate)
    
    def get_action(self, state):
        state = Variable(torch.from_numpy(state).float().unsqueeze(0))
        action = self.actor.forward(state)
        action = action.detach().numpy()[0,0]
        return action
    
    def update(self, batch_size):
        states, actions, rewards, next_states, _ = self.memory.sample(batch_size)
        states = torch.FloatTensor(states)
        actions = torch.FloatTensor(actions)
        rewards = torch.FloatTensor(rewards)
        next_states = torch.FloatTensor(next_states)
    
        # Critic loss        
        Qvals = self.critic.forward(states, actions)
        next_actions = self.actor_target.forward(next_states)
        next_Q = self.critic_target.forward(next_states, next_actions.detach())
        Qprime = rewards + self.gamma * next_Q
        critic_loss = self.critic_criterion(Qvals, Qprime)

        # Actor loss
        policy_loss = -self.critic.forward(states, self.actor.forward(states)).mean()
        
        # update networks
        self.actor_optimizer.zero_grad()
        policy_loss.backward()
        self.actor_optimizer.step()

        self.critic_optimizer.zero_grad()
        critic_loss.backward() 
        self.critic_optimizer.step()

        # update target networks 
        for target_param, param in zip(self.actor_target.parameters(), self.actor.parameters()):
            target_param.data.copy_(param.data * self.tau + target_param.data * (1.0 - self.tau))
       
        for target_param, param in zip(self.critic_target.parameters(), self.critic.parameters()):
            target_param.data.copy_(param.data * self.tau + target_param.data * (1.0 - self.tau))

更多代码可参考

ghliu/pytorch-ddpg: Implementation of the Deep Deterministic Policy Gradient (DDPG) using PyTorch (github.com)https://github.com/ghliu/pytorch-ddpg?

参考文献

【1】Deep Deterministic Policy Gradients Explained | by Chris Yoon | Towards Data Science

【2】强化学习入门：基本思想和经典算法 - 张浩在路上 (imzhanghao.com)

【3】?[RL] ???? ????: (4) DDPG (tistory.com)

【4】Deep Deterministic Policy Gradient(DDPG) — an off-policy Reinforcement Learning algorithm | by Dhanoop Karunakaran | Intro to Artificial Intelligence | Medium?