Tensorflow之逻辑回归与交叉熵

一、前言

线性回归预测的是一个连续值，而逻辑回归预测给出的是“是”和“否”的答案。

比如在使用激活函数sigmoid时，它是一个概率分配函数，在给定特征值时，特征值与权重的乘积作为输出值，映射到[0,1]区间，神经网络本质是一个表示/映射网络，由多层感知器组成，经过一层一层的映射，最后可把[0,1]间的这个值看成是神经网络给出的概率结果。

但对于逻辑回归，平方差损失函数刻画原有数据集与损失为同一数量级的情况下。

eg: 若真实值回答为1，但实际神经网络给出的值为一小数0.3，刻画损失为0.7。

但若特征值取值庞大，但实际神经网络的输出值很大时，所刻画的损失会很小，所以若使用平方差损失函数进行刻画时，则需要迭代次数较多，训练较慢。

对于分类问题，我们最好使用交叉熵损失函数会更有效，交叉熵会输出一个更大的“损失”。

交叉熵刻画的是实际输出（概率）与期望输出（概率）的距离，也就是说交叉熵值越小，两个概率分布就越接近。若概率分布p为期望输出，概率分布q为实际输出，H(p,q)为交叉熵，则有：

当然，在tf.keras中，使用binary_crossentropy计算二元交叉熵。?

二、逻辑回归与交叉熵实例

问题描述：在给定的数据集中，判断是否有欺诈行为，可以将其看成一个分类问题，将0-14列数据作为特征值，最后一列数据作为结果输出，通过查看损失函数以及成功率判断训练结果。

1、导入包

import tensorflow as tf
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

2、导入数据集

data = pd.read_csv('dataset/credit.csv',header = None)
data.head()   #显示前5行

数据集前5行数据如图1所示，

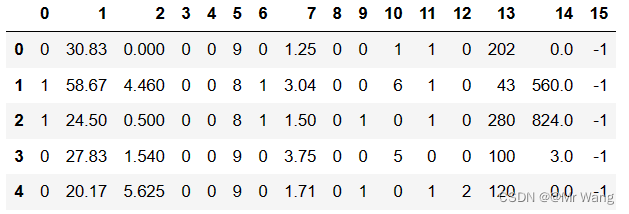
3、设置特征与输出

data.iloc[:,-1].value_counts()    #可对最后一列1与-1个数进行计数

x = data.iloc[:,:-1]              #iloc即为按照index取值
y = data.iloc[:,-1].replace(-1,0) #把-1用0代替，则用0，1表示是否有欺诈

4、创建模型

model = tf.keras.Sequential()#建立一个顺序模型
model.add(tf.keras.layers.Dense(4,input_shape = (15,),activation = 'relu')) #添加两个隐藏层
model.add(tf.keras.layers.Dense(4,activation = 'relu'))  
model.add(tf.keras.layers.Dense(1,activation = 'sigmoid'))#添加输出层，激活函数使用sigmoid，输出作为一个概率
model.summary()  #显示模型结构

?模型总体结构如图2所示，总共有3层，两个隐含层和一个输出层，Param为64则代表(15+1)*4=64,对应为15个特征加上一个偏置一共为16个参数，第一个隐藏层对应4个神经元，所以共有64个参数；Param为20则代表（4+1）*4=20个参数；Param为5则代表（4+1）共有5个参数。

5、编译并训练模型

#编译
model.compile(optimizer = 'adam',
              loss = 'binary_crossentropy',
              metrics = ['acc']      #计算成功率的
)

history = model.fit(x,y,epochs=100)  #训练100次

history.history.keys() #记录了loss和acc的变化
plt.plot(history.epoch,history.history.get('loss'))#绘制loss变化图
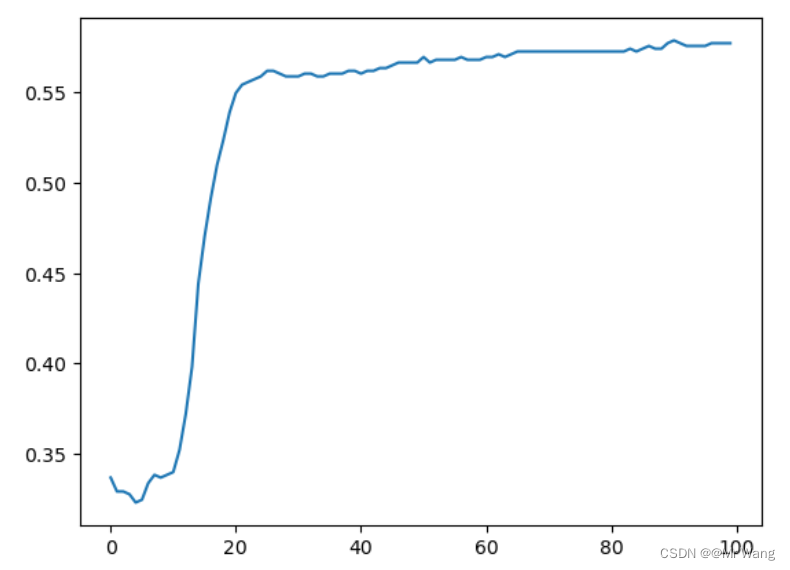
plt.plot(history.epoch,history.history.get('acc')) #绘图acc变化图

?如图3，4所示，分别为损失函数以及成功率随着训练次数发生的变化，损失函数从训练20次之后，损失loss的减小速度越来越小，但持续在减少；成功率acc随训练次数增加在逐渐增加。整体从损失以及成功率来考虑，模型训练还可以。

感谢关注与支持，将持续更新。