Codeforces Round 917 (Div. 2)(A~D)
A - Least Product
Solution
观察发现,对于 a i < 0 a_i<0 ai?<0,操作后 a i a_i ai? 不会变得更小, a i > 0 a_i>0 ai?>0,操作后 a i a_i ai? 不会变得更大。所以,当 ∏ i = 1 n a i ≥ 0 \prod_{i=1}^na_i\ge 0 ∏i=1n?ai?≥0 时,不可能变得更大; ∏ i = 1 n a i < 0 \prod_{i=1}^na_i<0 ∏i=1n?ai?<0 时,最优即为将 1 1 1 个数变为 0 0 0,这样可以保证操作次数最少。
A t t e n t i o n : \mathrm{Attention: } Attention: 不能将所有数相乘,因为乘积会超级大(最多也就 9 100 9^{100} 9100 位吧),所以需要记录负数的个数和是否有 0 0 0,来进行判断
Code
#include <iostream>
#define int long long
using namespace std;
typedef pair<int, int> PII;
const int SIZE = 1e2 + 10;
int N;
int A[SIZE];
void solve()
{
cin >> N;
int Zero = 0, Less = 0;
for (int i = 1; i <= N; i ++)
{
cin >> A[i];
if (A[i] == 0) Zero = 1;
else if (A[i] < 0) Less ++;
}
if ((Less % 2) == 0 && !Zero)
cout << 1 << endl << 1 << " " << 0 << endl;
else
cout << 0 << endl;
}
signed main()
{
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(0);
int Data;
cin >> Data;
while (Data --)
solve();
return 0;
}
B - Erase First or Second Letter
Solution
暴力出奇迹,打表出省一
Way 1(打表找规律)
打表也需要技巧:
第 1 1 1 步:写出暴力代码
S = ' ' + S;
int Cnt = 0;
map<string, int> Vis;
queue<string> Q;
Q.push(S);
while (Q.size())
{
string S2 = Q.front();
Q.pop();
if (Vis.count(S2) || S2.size() == 1) continue;
Vis[S2] = 1;
Cnt ++;
string S3 = S2;
S3.erase(1, 1);
Q.push(S3);
S3 = S2;
if (S3.size() > 2) S3.erase(2, 1);
Q.push(S3);
}
cout << Cnt << endl;
第 2 2 2 步:观察如果整个序列无重复元素的时候的值: ( 1 + n ) ? n 2 \frac{(1+n)\cdot n}{2} 2(1+n)?n?
第 3 3 3 步:观察对于一个无重复元素的序列,加入重复元素的变化(难点)
通过,不断的尝试,可以发现规律:对于字母 a a a,如有重复数字,则为 n n n ? - ? ∑ i = 1 n i ? P a ? 1 [ S i = a ] \sum_{i=1}^n i-P_a-1[S_i=a] ∑i=1n?i?Pa??1[Si?=a],其中 P a P_a Pa? 为字母 a a a 第一次出现的下标, [ ] [] [] 表示条件。
最后,通过容斥原理得,最终值为 ( 1 + n ) ? n 2 ? ∑ i = a z ∑ j = 1 n j ? P i ? 1 [ S j = i ] \frac{(1+n)\cdot n}{2}-\sum_{i=a}^z\sum_{j=1}^n j-P_i-1[S_j=i] 2(1+n)?n??∑i=az?∑j=1n?j?Pi??1[Sj?=i]
由于 n n n 比较大,故通过前缀和优化即可。
Code 1
#include <iostream>
#include <map>
#include <set>
#include <cstring>
#include <queue>
#define int long long
using namespace std;
typedef pair<int, int> PII;
const int SIZE = 1e5 + 10;
int N;
string S;
int Cnt[27], Num[27], P[27];
void solve()
{
cin >> N >> S;
S = ' ' + S;
memset(Cnt, 0, sizeof Cnt);
memset(Num, 0, sizeof Num);
memset(P, 0, sizeof P);
for (int i = 1; i <= N; i ++)
if (!P[S[i] - 'a'])
P[S[i] - 'a'] = i;
int Result = (1 + N) * N / 2;
for (int i = N; i >= 1; i --)
if (P[S[i] - 'a'] == i)
Result -= (N * Num[S[i] - 'a'] - (Cnt[S[i] - 'a'] - Num[S[i] - 'a'] * i - Num[S[i] - 'a']) - i * Num[S[i] - 'a']);
else
Cnt[S[i] - 'a'] += i, Num[S[i] - 'a'] ++;
cout << Result << endl;
}
signed main()
{
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(0);
int Data;
cin >> Data;
while (Data --)
solve();
return 0;
}
方法很土,但是如果大家想要用总数 ? - ? 重复的数,那么可以借鉴一下,不过我不会证(*/ω\*)
Way 2(思维)
考虑对于
1
1
1 个字符串:bcdaaaabcdaaaa
-
D
e
l
\mathrm{Del}
Del
b, D e l \mathrm{Del} Delc, … \dots … 共 14 14 14 种 - 保留
b, D e l \mathrm{Del} Delc, D e l \mathrm{Del} Deld, … \dots … 共 13 13 13 种 -
D
e
l
\mathrm{Del}
Del
b,保留c, D e l \mathrm{Del} Deld, D e l \mathrm{Del} Dela, … \dots … 共 12 12 12 种 -
D
e
l
\mathrm{Del}
Del
b, D e l \mathrm{Del} Delc,保留d, D e l \mathrm{Del} Dela, D e l \mathrm{Del} Dela, … \dots … 共 11 11 11 种
大家可以发现此时相加已经是 50 50 50 了(样例 4 4 4)
这说明,只有当该字符为第 1 1 1 次出现时,才会对答案产生 n ? i + 1 n-i+1 n?i+1 的贡献。
P r o o f : \mathrm{Proof:} Proof: 若总共操作 k k k 次删第 1 1 1 个字符得到一个非第一次出现的字符 x x x(位置为 i i i),那么这个操作等价于不断地删第 1 1 1 个字符直到当前字符串的第 1 1 1 个字符是第一次出现的字符 x x x,然后不断地删第 2 2 2 个字符直到删掉第 i i i 字符。此时前后 2 2 2 种操作得到的字符串是一样的,所以 i i i 能得到的所有字符串,都能由第一次出现字符 x x x 的位置通过操作来得到。故,会计算重复。
综上所述,最终的值为: ∑ i = a z n ? P i + 1 \sum_{i=a}^z n-P_i+1 ∑i=az?n?Pi?+1
其中, P i P_i Pi? 为字符 i i i 出现的下标。
Code 2
#include <iostream>
#include <map>
#include <set>
#include <cstring>
#include <queue>
#define int long long
using namespace std;
typedef pair<int, int> PII;
int N;
string S;
int P[27];
void solve()
{
cin >> N >> S;
S = ' ' + S;
memset(P, 0, sizeof P);
for (int i = 1; i <= N; i ++)
if (!P[S[i] - 'a'])
P[S[i] - 'a'] = i;
int Result = 0;
for (int i = 1; i <= N; i ++)
if (P[S[i] - 'a'] == i)
Result += N - i + 1;
cout << Result << endl;
}
signed main()
{
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(0);
int Data;
cin >> Data;
while (Data --)
solve();
return 0;
}
C - Watering an Array
Solution
性质:当 a a a 数组全部第 1 1 1 次变为 0 0 0 后,之后一定是加 1 1 1 次,统计 1 1 1 次。
P r o o f : \mathrm{Proof:} Proof: 因为对于全 0 0 0 的数组,无论怎么加,一定都不会超过 1 1 1。故倒不如加 1 1 1 次,位置 1 1 1 一定满足,再统计即可。
所以,我们只需要考虑初始的 a a a 数组加多少次,才能价值最高。变为全 0 0 0 数组之后的价值就是 ? 剩余的天数 2 ? \lfloor\frac{剩余的天数}{2}\rfloor ?2剩余的天数??, 2 2 2 个权值相加即可。
这里,直接枚举即可,具体看代码吧!
Code
#include <iostream>
#define int long long
using namespace std;
typedef pair<int, int> PII;
const int SIZE1 = 2e3 + 10, SIZE2 = 1e5 + 10;
int N, K, D;
int A[SIZE1], V[SIZE2];
void solve()
{
cin >> N >> K >> D;
for (int i = 1; i <= N; i ++)
cin >> A[i];
for (int i = 1; i <= K; i ++)
cin >> V[i];
int Over = 0; //记录前面哪些点是无用的,保证时间复杂度
for (int i = 1; i <= N; i ++)
if (A[i] > i)
Over = i;
else break;
int Result = 0;
for (int i = 1; i <= N; i ++)
if (A[i] == i)
Result ++;
Result += (D - 1) / 2;
for (int k = 1; k <= N; k ++) //下面可能不止需循环 1 次,因为天数较多,K 很小的时候需要多次,但一定不会超过 N(被 fst 了,哭~~~)
for (int i = 1; i <= min(K, D); i ++)
{
if (V[i] <= Over) continue; //说明不用再更新了
for (int j = Over + 1; j <= V[i]; j ++) //更新
A[j] ++;
int Cnt = 0;
for (int j = Over + 1; j <= N; j ++) //统计
if (A[j] == j)
Cnt ++;
if ((i + (k - 1) * min(K, D)) < D && Cnt + (D - (i + (k - 1) * min(K, D)) - 1) / 2 > Result) //取最大
Result = Cnt + (D - (i + (k - 1) * min(K, D)) - 1) / 2;
for (int j = Over + 1; j <= V[i]; j ++) //更新无用点
if (A[j] > j)
Over = j;
else break;
}
cout << Result << endl;
}
signed main()
{
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(0);
int Data;
cin >> Data;
while (Data --)
solve();
return 0;
}
D - Yet Another Inversions Problem
Solution
首先,考虑对于每 k k k 个数内部有多少个逆序对,通过归并排序或树状数组即可求出。
那么,由于 q q q 是一个 0 ~ k ? 1 0\sim k-1 0~k?1 的排列,所以 0 ~ k ? 1 0\sim k-1 0~k?1 一定是都有的。下面,就需要求出对于任意 2 2 2 个数 p i , p j p_i,p_j pi?,pj? 能够产生多少个逆序对。
由于,对于每 1 1 1 个 p i p_i pi?,都可以分解为 k k k 个: p i , 2 p i , 4 p i , 8 p i … p_i,2p_i,4p_i,8p_i\dots pi?,2pi?,4pi?,8pi?…。所以,可以考虑 乘 2 2 2 或 除 2 2 2 来判断,考虑对 p i p_i pi? 不断除 2 2 2,如果除 2 2 2 之后还是大于 p j p_j pj?,那么个数会多 k ? c n t k-cnt k?cnt( c n t cnt cnt 表示除了多少次)
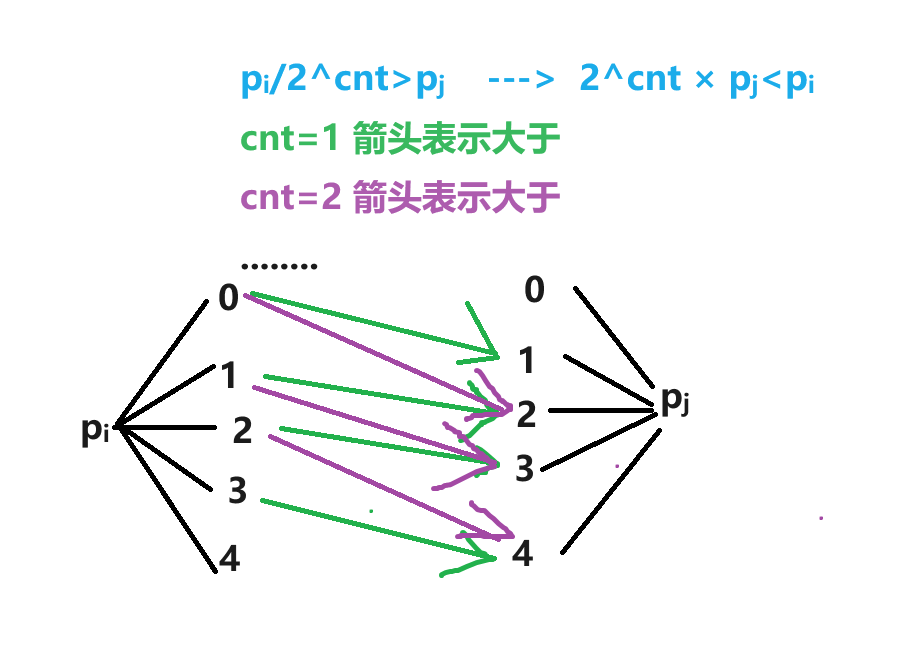
如图所示, k = 5 k=5 k=5, c n t cnt cnt 其实就意味着比当前倍数大 2 c n t 2^{cnt} 2cnt 的 p j p_j pj? 还大,那符合条件的当前倍数的个数为 k ? c n t k-cnt k?cnt,故贡献为 k ? c n t k-cnt k?cnt。
对应着,还有不断乘 2 2 2,这就是再找 2 k p i > 2 k ? c n t p j 2^kp_i>2^{k-cnt}p_j 2kpi?>2k?cntpj?,与上面的方法类似,箭头只是不断朝右上方罢了,大家可以自己画画,最后的贡献还是 k ? c n t k-cnt k?cnt
不过,这样是 O ( n 2 ) O(n^2) O(n2),所以考虑优化。
观察可知,在枚举 p j p_j pj? 的时候浪费了时间,所以可以用树状数组存储 p j p_j pj?,然后可以做到 O ( log ? n ) O(\log n) O(logn) 的时间复杂度查询,那么贡献就变为了:个数 × \times × ( k ? c n t ) (k-cnt) (k?cnt)
具体看代码吧(qwq)
Code
#include <iostream>
#include <cstring>
#define lowbit(x) x & -x
#define int long long
using namespace std;
typedef pair<int, int> PII;
const int SIZE = 4e5 + 10, MOD = 998244353;
int N, K;
int P[SIZE], Q[SIZE];
struct Fenwick
{
int Tree[SIZE];
void Add(int x, int d) { for (int i = x; i < SIZE; i += lowbit(i)) Tree[i] += d; }
int Sum(int x)
{
int Result = 0;
for (int i = x; i; i -= lowbit(i))
Result += Tree[i];
return Result;
}
}Inv, Count;
int Quick_Pow(int a, int b, int p)
{
int Result = 1;
while (b)
{
if (b & 1) Result = Result * a % p;
a = a * a % p;
b >>= 1;
}
return Result;
}
void solve()
{
cin >> N >> K;
for (int i = 1; i <= K; i ++)
Inv.Tree[i] = 0;
for (int i = 1; i <= N * 2; i ++)
Count.Tree[i] = 0;
int Result = 0;
for (int i = 1; i <= N; i ++)
cin >> P[i];
for (int i = 1; i <= K; i ++)
cin >> Q[i], Q[i] ++, Result += Inv.Sum(K) - Inv.Sum(Q[i]), Inv.Add(Q[i], 1);
Result = Result * N % MOD;
for (int i = N; i >= 1; i --)
{
int Num = P[i], Cnt = 0;
while (Num && Cnt < K)
{
Result = (Result + Count.Sum(Num) * (K - Cnt) % MOD) % MOD;
Num >>= 1;
Cnt ++;
}
Num = P[i] * 2, Cnt = 1;
while (Cnt < K)
{
if (Num > 2 * N) //这里注意,> 2 * N 了,后面肯定都比所有数大,可以直接算出来,用等差数列求和公式(因为变的只有 Cnt 了,每次减 1,公差为 1)
{
Result = (Result + (N - i) * (1 + K - Cnt) % MOD * (K - Cnt) % MOD * Quick_Pow(2, MOD - 2, MOD) % MOD) % MOD;
break;
}
Result = (Result + Count.Sum(Num) * (K - Cnt) % MOD) % MOD;
Num <<= 1;
Cnt ++;
}
Count.Add(P[i], 1);
}
cout << Result << endl;
}
signed main()
{
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(0);
int Data;
cin >> Data;
while (Data --)
solve();
return 0;
}
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!