【复习】人工智能 第四章 不确定性推理

一、可信度方法（重点）

优点：直观、简单，且效果好

（1）结构：

IF ??E ???THEN ???H ???（CF（H,E））

（CF（H,E））：可信度因子

表示当 E 所对应的证据为真时对 H 的影响程度 ，取值范围: [-1,1]，越大越真。

若确定为真，则为1；若肯定它为假，则为–1。

例：IF ??头痛 ???AND ????流涕 ??????THEN ????感冒 ?（0.7）

（2）合成两条结论相同的不确定算法（重点）

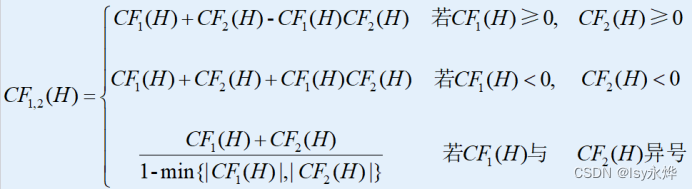
?例：

二、概率分配函数（重点）

例如，设 A={红}， M（A）=0.3，则命题“x是红色”的信任度是0.3。

设 D = {红，黄，蓝}

M（{红}）= 0.3， M（{黄}）= 0， M（{蓝}）= 0.1，

M（{红，黄}）= 0.2，M（{红，蓝}）= 0.2，

M（{黄，蓝}）= 0.1，M（{红，黄，蓝}）= 0.1，M（Φ）= 0

但：M（{红}）+ M（{黄}）+ M（{蓝}）= 0.4

故概率分配函数的总概率不一定为1。

三、信任函数（重点）

Bel（A）：对命题A为真的总的信任程度。

例：设 D ={红，黄，蓝}

M（{红}）= 0.3， M（{黄}）= 0，M（{红，黄}）= 0.2，求Bel（{红，黄}）

Bel（{红，黄}）= Bel（{红}） + Bel（{黄}） + Bel（{红，黄}）

= 0.3 + 0 + 0.2 = 0.5

四、似然函数（重点）

Pl（A）：表示A不为假的程度

Pl（A） = 1 - Bel（?A）

对于上一个例题，继续计算可得：

Pl（{蓝}）= 1 - Bel（?{蓝}）= 1 - Bel（?{红，黄}） = 1 - 0.5 = 0.5

显然，A不为假，并不代表A一定为真，也就是说对A不为假的信任程度应该大于对A为真的信任程度，即有：?Pl(A)≥Bel(A)

五、概率分配函数的正交和（不确定考不考）

注意是求乘法的时候是，交错相乘，多找几遍规律，注意一下下标（尤其是下标，一定要看下标），其他都是类似算法。

例：