矩阵行列式的四大应用

目录

一. 介绍

二. 行列式的基本性质

2.1 单位阵的行列式

2.2 交换行位置的行列式

三. 矩阵求逆与行列式

四. 体积与行列式

五. 矩阵主元与行列式

六. 解方程与矩阵行列式

七. 小结

---

一. 介绍

行列式可以反应矩阵的很多性质，比如可以求矩阵的逆，也可以求方程的解，如下：

矩阵行列式有三个基础的性质：

（1）单位阵

单位阵的行列式为1，也就是：

det I=1

（2) 符号

矩阵的行位置交换会影响行列式的符号

（3）线性关系

矩阵行列式与行向量之间呈现线性关系

本文章将梳理矩阵行列式的四个基本应用。

二. 行列式的基本性质

以2行2列的矩阵为例，其行列式的计算非常简单，如下：

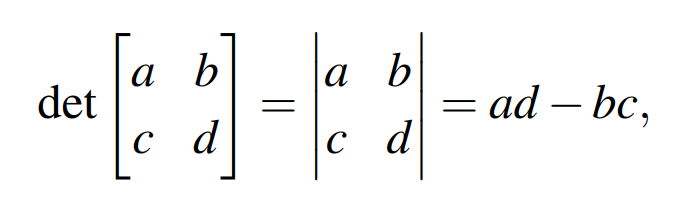
通常行列式有两种常用写法，分别是detA和|A|

以下我们将主要讨论方阵。

2.1 单位阵的行列式

很明显单位矩阵（identity matrix）的行列式为1，如下：

2.2 交换行位置的行列式

当把某两行的位置交换时，行列式会改变符号，如下：

任何置换矩阵都可以变成单位阵，单位阵的行列式为1，由此可得置换矩阵的行列式只能取1或-1，如下：

三. 矩阵求逆与行列式

我们都知道如果矩阵行列式为0时，那么其为奇异矩阵（singular）。如果矩阵A行列式不为0，那么该矩阵可以直接求逆，如下：

逆矩阵中的元素与行列式的倒数相关。

在求矩阵特征值时，涉及到：

其中的值会出现在矩阵对角线上，要保证该方程有解，那么要求是奇异的，也就是可得：

把以上等式看成一个方程，如果该方程为n次方，也就是有n个解，从而矩阵A有n个特征值。

四. 体积与行列式

以最简单的三维立方体为例子dV=dxdydz，也就是：

如果写成柱坐标（cylindrical coordinates），可得：

dx的积分运算替换成(dx/du)du，由此可得体积运算为：

于是，雅克比行列式（Jacobian determinant）就可以写成三维的形式，如下：

此三阶矩阵的行列式很容易计算为r

综上可得矩阵A的行列式与n维箱子的体积相等，在网络安全中此结论是很有用的，来看一个直观的图形：

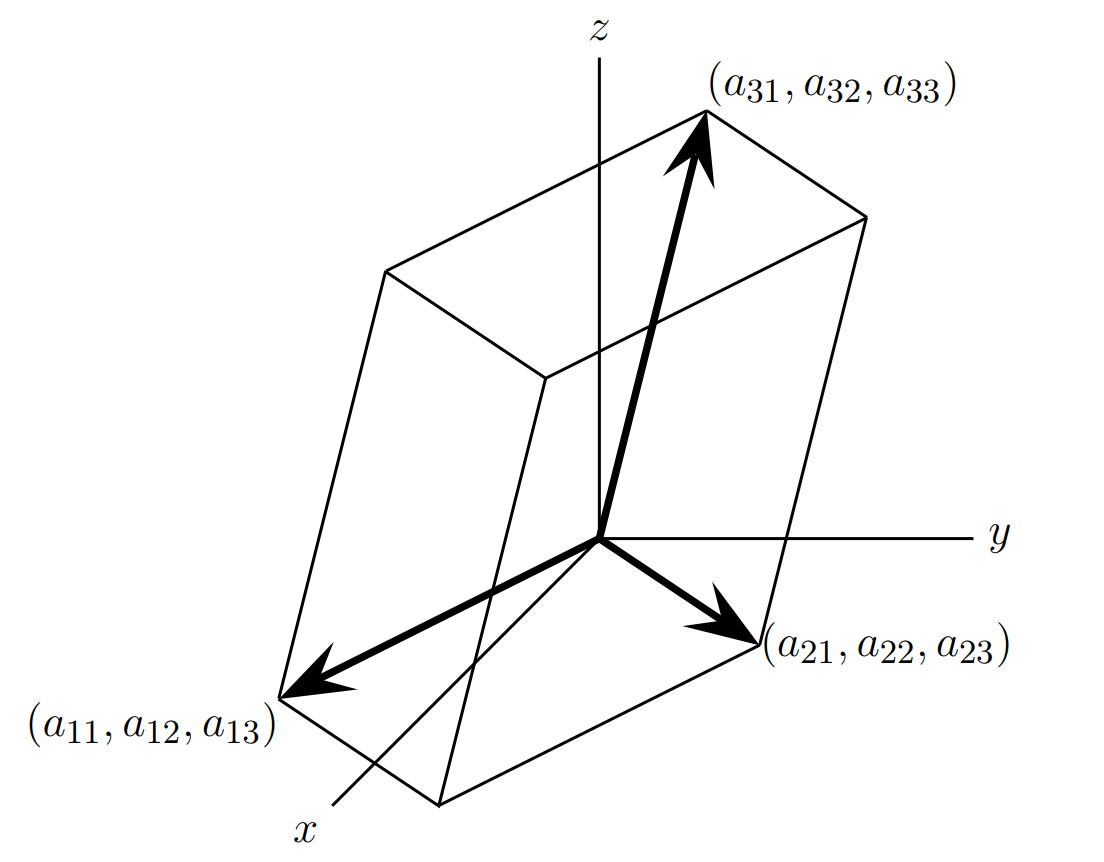
五. 矩阵主元与行列式

忽略正负号的情况下，矩阵行列式等于矩阵主元（pivots)的乘积。?

六. 解方程与矩阵行列式

可以用行列式的思想来衡量b对的影响。利用行列式可以直接计算矩阵A的逆，接着利用Cramer法则计算解：

七. 小结

以上讨论中，我们了解到行列式的值与主元的乘积相关。通常而言计算行列式有两个常用的公式，一个是所谓的big formula，另外一个是 formula by induction。

（1）线性代数需要掌握的重点

行列式 内容：行列式的定义和性质；Cramer 法则；子式与代数余子式；按一行（列）展开定理。

要求： 掌握行列式的概念和性质，熟练应用行列式的性质计算行列式，并会用行列式求解线性方程组。

矩阵及其运算、矩阵的初等变换与线性方程组 内容： 矩阵的概念和运算；常用的特殊矩阵；矩阵的初等变换与初等矩阵；可逆矩阵以及性质 ；矩阵的秩等概念。 线性方程组的解。

要求： 掌握矩阵和秩的概念；能熟练地进行矩阵的各种运算（加、减、数乘、乘、求逆等）；会求逆阵和矩阵的秩。

向量组的线性相关性 内容： 向量组及其线性组合、向量组的线性相关性，向量组的秩，线性方程组的解的结构，向量空间。

要求： 掌握向量的线性关系（组合与等价、线性相关与线性无关、极大线性无关组）等概念， 能熟练应用矩阵来求解或讨论线性方程组的解和解的结构。掌握向量空间的有关知识。

（2）矩阵应用

随着计算机硬件的发展和处理复杂算法能力的提高 ，近30年来 ，以人工智能为核心的相关学科群 ：计算机视觉 、模式识别（含机器学习） 、数字图像处理 、数字信号处理和计算机图形学得到了迅速的发展 ．20世纪90年代 ，这些学科的发展逐步走向成熟 ，相关技术的融合和实际应用显著增长 ．而且 ，随着计算机应用深入到社会科学和生物学等学科 ，加之计算机网络的迅速扩展 ，数据的维数激增和数据量按指数增长 ，计算机所处理的数据发生了根本性的变化 ，这些都将进一步推动相关学科向纵深发展 ． 在这些学科研究的过程中 ，涉及数学知识的广度和深度都超出了人们的想象 ．

在广度上 ，几乎所有数学科目都在这些学科的研究中出现过 ，而不像传统的学科 ， 如物理主要应用微分几何 、偏微分方程和群论 ；不仅如此 ，这些学科研究过程中所用的数学理论往往是当前数学界最新的研究成果 ，比如图像处理中所用的偏微分方程理论 ．这对没有受过严格数学训练的计算机学者提出了严峻挑战 ． 传统的计算机学科研究所用到的数学主要集中在离散数学 、算法设计 、数值计算和组合数学 ，这些19世纪的数学已经无法满足当前计算机科学发展的要求 ．为此 ，众多的计算机学者一方面呼吁数学工作者加入到计算机科学的研究中 ，同时也积极地将相关的数学理论引入到研究中。

矩阵计算又称为数值线性代数 ．作为一门数学学科 ，它是众多理工学科重要的数学工具 ．矩阵理论既是经典数学的基础课程 ，是一门最有实用价值的数学理论 ，是计算机科学与工程计算的核心 ，已成为现代各科技领域处理大量有限维空间形式与数量关系强有力的工具 ，计算机科学和工程的问题最终都转化成矩阵的运算与求解 ．特别是计算机的广泛应用为矩阵论的应用开辟了广阔的前景 ．例如 ，系统工程 、优化方法以及稳定性理论等 ，都与矩阵论有着密切的联系。