计算图与动态图机制

一、计算图

计算图是用来描述运算的有向无环图

计算图有两个主要元素：结点（Node）和边（Edge）

• 结点表示数据，如向量，矩阵，张量
• 边表示运算，如加减乘除卷积等

用计算图表示：

• y = (x+ w) * (w+1)
• a = x + w
• b = w + 1
• y = a * b

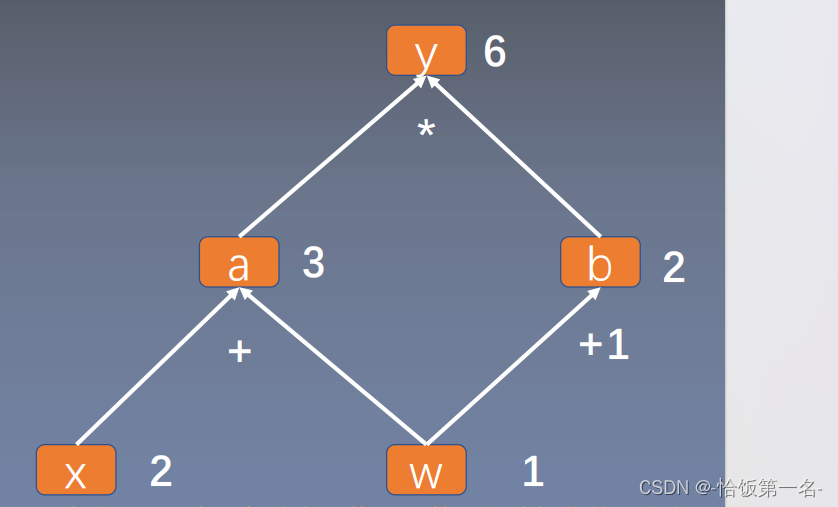
y = (x + w) * (w + 1)
a = x + w
b = w + 1
y = a * b
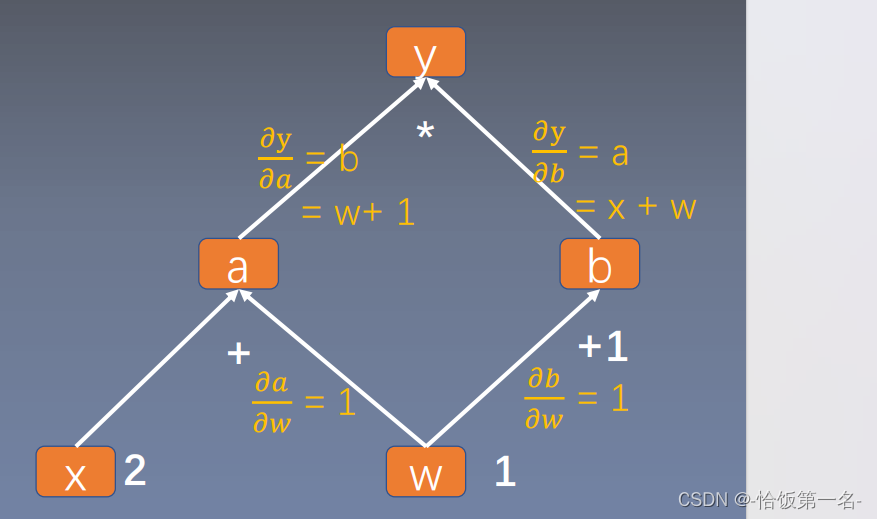
?y/?w = (?y/?a) * (?a/?w) + (?y/?b) * (?b/?w)
       = b * 1 + a * 1
       = b + a
       = (w + 1) + (x + w)
       = 2w + x + 1
       = 2 * 1 + 2 + 1
       = 5

计算图与梯度求导 y = (x+ w) * (w+1)

叶子结点：用户创建的结点称为叶子结点，如X 与 W

is_leaf: 指示张量是否为叶子结点

grad_fn: 记录创建该张量时所用的方法（函数）
y.grad_fn =
a.grad_fn =
b.grad_fn =

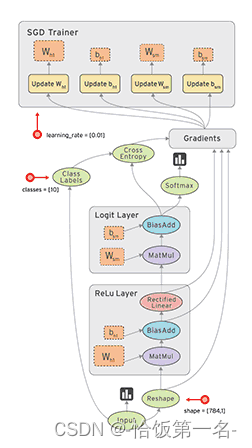
动态图

动态图vs 静态图

动态图 PyTorch

静态图 TensorFlow

import torch
w = torch.tensor([1.], requires_grad=True)  # 创建张量w，并设置requires_grad=True以计算梯度
x = torch.tensor([2.], requires_grad=True)  # 创建张量x，并设置requires_grad=True以计算梯度

a = torch.add(w, x)     # 执行加法操作，计算w + x，得到张量a
b = torch.add(w, 1)     # 执行加法操作，计算w + 1，得到张量b
y = torch.mul(a, b)     # 执行乘法操作，计算a * b，得到张量y

y.backward()            # 自动计算y对所有需要梯度的叶子结点的梯度
print(w.grad)           # 打印w的梯度

# 查看叶子结点
# print("is_leaf:\n", w.is_leaf, x.is_leaf, a.is_leaf, b.is_leaf, y.is_leaf)

# 查看梯度
# print("gradient:\n", w.grad, x.grad, a.grad, b.grad, y.grad)

# 查看 grad_fn
print("grad_fn:\n", w.grad_fn, x.grad_fn, a.grad_fn, b.grad_fn, y.grad_fn)

在这段代码中，我们定义了两个张量w和x，并且将它们设置为需要计算梯度（requires_grad=True）。然后我们定义了计算图中的各个操作：加法a = w + x，加法b = w + 1，乘法y = a * b。
接下来，我们调用y.backward()来自动计算y对于所有需要梯度的叶子结点的梯度。在这个例子中，叶子结点是w和x。然后，我们打印出w的梯度w.grad。
运行这段代码，我们得到的输出是tensor([5.])，即w的梯度为5。