Java 数据结构篇-实现 AVL 树的核心方法

🔥博客主页：?【小扳_-CSDN博客】
?感谢大家点赞👍收藏?评论??

文章目录

? ? ? ? 1.0 AVL 树的说明

? ? ? ? 2.0 AVL 树的成员变量及其构造方法

? ? ? ? 3.0 实现 AVL 树的核心方法

? ? ? ? 3.1 获取当前节点的高度 height(AVLNode node)

? ? ? ? 3.2 更新当前节点的高度 updateHeight(AVLNode node)

? ? ? ? 3.3 平衡因子 bf(AVLNode node)

? ? ? ? 3.4 对失衡节点旋转 rotate(AVLNode node)

? ? ? ? 3.5 检查节点是否平衡，重新平衡 balance(AVLNode node)?

? ? ? ? 3.6 插入、更新节点?put(int key, Object value)

????????3.7 删除节点 remove (AVLNode node)

? ? ? ? 4.0 实现 AVLTree 核心方法的完整代码

---

?

? ? ? ? 1.0 AVL 树的说明

????????AVL树是一种自平衡二叉搜索树，它的名称来源于它的发明者 Adelson-Velsky 和 Landis 。在AVL树中，任何节点的两个子树的高度最多相差 1，这使得AVL树能够保持相对平衡，从而保证了树的查找、插入和删除操作的时间复杂度都是 O(log n)?。

????????AVL树的平衡性是通过对节点进行旋转操作来实现的，包括左旋、右旋、左右旋和右左旋。当插入或删除节点后破坏了AVL树的平衡性时，就会进行相应的旋转操作来保持树的平衡。

? ? ? ? 也就是说， AVL 树是一种特殊的自平衡二叉搜索树。

? ? ? ??

? ? ? ? 2.0 AVL 树的成员变量及其构造方法

? ? ? ? （1）构造 AVLNode 内部类变量 ：

? ? ? ? ????????int key 关键字：通过关键字来比较每个节点的大小。

? ? ? ? ????????Object value 值：通过该变量存放值。

? ? ? ? ????????AVLNode left：引用左孩子节点。

? ? ? ? ????????AVLNode right：引用右孩子节点。

? ? ? ? ? ? ? ? int height 高度：表示当前节点的高度，默认初始化为 1 。

? ? ? ? （2）AVLNode 内部类构造方法：

? ? ? ? ? ? ? ? 重载两个内部类的构造方法分别为：参数为 key，value 的构造方法、参数为 key，value，left，right 的构造方法。

? ? ? ? （3）构造 AVLTree 外部类 ：

? ? ? ? ? ? ? ? AVLNode root：表示该树的头节点。

代码如下：

public class AVLTree {

    AVLNode root = null;

    static class AVLNode {
        int key;
        Object value;
        AVLNode left;
        AVLNode right;
        int height = 1;

        public AVLNode(int key, Object value) {
            this.key = key;
            this.value = value;
        }

        public AVLNode(int key, Object value, AVLNode left, AVLNode right) {
            this.key = key;
            this.value = value;
            this.left = left;
            this.right = right;
        }
    }

}

? ? ? ? 3.0 实现 AVL 树的核心方法

? ? ? ? AVL 树的最核心的方法就是插入、更新、删除操作，因为这些操作都有可能造成二叉搜索树失去平衡。为了解决自平衡的特点，需要每一个插入或者更新、删除操作之后，需要检查是否失去平衡，若失去平衡需要通过左旋、右旋、左右旋、右左旋来重新达到平衡状态；若没有失去平衡，无需任何操作。

? ? ? ? 3.1 获取当前节点的高度 height(AVLNode node)

? ? ? ? 不能直接通过 node.height 得到当前节点的高度，是因为默认高度为 1，若出现该节点为 null 时，就会出现矛盾，因此需要先判断该节点是否为 null 节点，若为空节点，返回 0 ；若不为 空节点，则返回当前节点 node.height 即可。

代码如下：

    //获取当前节点的高度
    private int height (AVLNode node) {
        return node == null ? 0 : node.height;
    }

?

? ? ? ? 3.2 更新当前节点的高度 updateHeight(AVLNode node)

? ? ? ? 由于通过删除、插入、旋转都有可能导致当前节点的高度发生改变，所以需要更新高度。实现该方法也很简单，判断当前节点的左右节点的高度，取最大的高度 + 1 就是为当前节点的高度。

代码如下：

    //更新当前的高度
    private void updateHeight (AVLNode node) {
        node.height = Integer.max(height(node.left),height(node.right)) + 1;
    }

? ? ? ? 3.3 平衡因子 bf(AVLNode node)

? ? ? ? 判断当前节点是否失去平衡，当该节点的左子树的高度 - 右子树的高度 > 1或者 < -1 即失去平衡了。若差值为 1、0、-1，表示没有失去平衡。

代码如下：

    //平衡因子
    private int bf (AVLNode node) {
        return  height(node.left) - height(node.right);
    }

? ? ? ? 3.4 对失衡节点旋转 rotate(AVLNode node)

? ? ? ? 有四种情况：左旋、右旋、左右旋、右左旋

? ? ? ? 左旋：需要先拿到失衡节点 node 的右孩子节点 node.right ,将 r = node.right 赋值给 r 。先将 r.left 赋值给 node.right ，即 node.right = r.left 进行 "换爹" 操作，然后再 "上位" r.left = node 。最后，因为旋转会导致当前 node 的节点与上位后的节点 r 的高度都有可能会改变，所以需要及时更新高度，通过 updateHeight(node)，updateHeight(r)，需要注意的是，更新的顺序不能改变。

? ? ? ? 右旋：跟左旋的原理是一样的，需要先拿到失衡节点 node 的左孩子节点 node.left ,将 l?= node.left?赋值给 l?。先将 l.right?赋值给 node.left?，即 node.left?= l.right?进行 "换爹" 操作，然后再 "上位" l.right?= node 。最后，因为旋转会导致当前 node 的节点与上位后的节点 r 的高度都有可能会改变，所以需要及时更新高度，通过 updateHeight(node)，updateHeight(l)，需要注意的是，更新的顺序不能改变。

? ? ? ? 左右旋：通过结合左旋、右旋实现左右旋。先拿到当前节点的左节点 l = node.left，对于 l 节点需要用到左旋的方法进行旋转 leftRotate(l)，旋转后需要重新赋值 node.left = leftRotate(l) 。接着对于 node 节点需用用到右旋方法进行旋转 rightRotate(node) 。最后返回?rightRotate(node) 节点即可。

? ? ? ? 右左旋：通过结合右旋、左旋实现右左旋。先拿到当前节点的右节点 r = node.right，对于 r 节点需要用到右旋的方法进行旋转 rightRotate(r) ，旋转后需要重新赋值 node.right = rightRotate(r) 。接着对于 node 节点需要用到左旋方法 leftRotate(node) 。最后返回 leftRotate(node) 节点即可。

代码如下：

    //左旋
    private AVLNode leftRotate (AVLNode node) {
        AVLNode r = node.right;
        node.right = r.left;
        r.left = node;
        updateHeight(node);
        updateHeight(r);
        return r;
    }

    //右旋
    private AVLNode rightRotate (AVLNode node) {
        AVLNode l = node.left;
        node.left = l.right;
        l.right = node;
        updateHeight(node);
        updateHeight(l);
        return l;
    }

    //左右旋
    private AVLNode leftRightRotate (AVLNode node) {
        AVLNode l = node.left;
        node.left = leftRotate(l);
        return rightRotate(node);
    }

    //右左旋
    private AVLNode rightLeftRotate (AVLNode node) {
        AVLNode r = node.right;
        node.right = rightRotate(r);
        return leftRotate(node);
    }

? ? ? ? 3.5 检查节点是否平衡，重新平衡 balance(AVLNode node)?

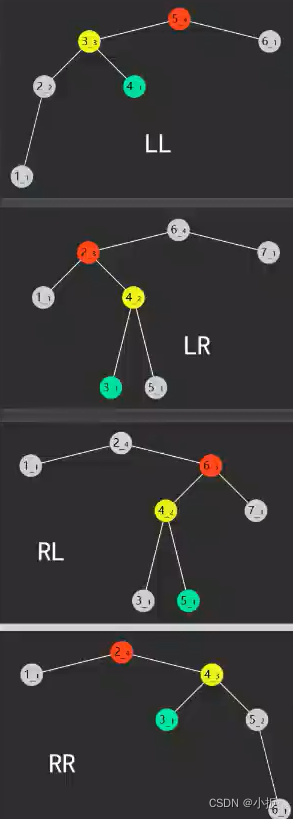
? ? ? ? 介绍四种失衡状态的树

? ? ? ? LL : 当前节点 node 的左子树的高度 - 右子树的高度 > 1，且 node.left 的左子树的高度 - node.left 的右子树的高度 >= 0 。实现该情况重新平衡，只需要当前节点进行右旋操作即可。

? ? ? ? LR：当前节点 node 的左子树的高度 - 右子树的高度 > 1，且 node.left 的左子树的高度 - node.left 的右子树的高度 < 0 。实现该情况重新平衡，需要进行先将 node.left 节点进行左旋，重新 node.left = leftRotate(node.left)，接着对于 node 进行右旋即可，也就是上面已经实现的左右旋方法。

? ? ? ? RL：当前节点 node 的左子树的高度 - 右子树的高度 < -1 ，且 node.right 的左子树的高度 - node.right?的右子树的高度 >?0 。实现该情况重新平衡，需要用到上面实现了的右左旋方法。

? ? ? ? RR：当前节点 node 的左子树的高度 - 右子树的高度 < -1 ，且 node.right 的左子树的高度 - node.right 的右子树的高度 <= 0 。实现该情况重新平衡，只需要左旋一次操作即可。

四种失衡状态图：

代码如下：

    //检查节点是否失衡，重新平衡代码
    private AVLNode balance (AVLNode node) {
        if(node == null) {
            return  null;
        }
        if (bf(node) > 1 && bf(node.left) >= 0) {
            return rightRotate(node);
        } else if (bf(node) > 1 && bf(node.left) < 0) {
            return leftRightRotate(node);

        } else if (bf(node) < -1 && bf(node.right) <= 0) {
            return leftRotate(node);

        }else if (bf(node) < -1 && bf(node.right) > 0) {
            return rightLeftRotate(node);
        }
        return node;
    }

? ? ? ? 当 node == null 时，返回 null 即可。

? ? ? ? 3.6 插入、更新节点?put(int key, Object value)

? ? ? ? 使用递归实现插入、更新节点。两种情况，若没有找到 key 关键字时，而找到空位的地方插入新节点；若找到 key 关键字时，更新该节点的值即可。区别于一般的二叉搜索树，自平衡的二叉搜索树，需要在插入节点后更新当前节点的高度和通过旋转来重新达到平衡。需要注意的是，更新节点的操作是不会改变高度还有破坏平衡。

代码如下：

    //更新
    public AVLNode put (int key, Object value) {
        return doPut(root,key,value);
    }

    private AVLNode doPut(AVLNode node, int key, Object value) {
        if (node == null) {
            return new AVLNode(key,value);
        }
        if (node.key == key) {
            node.value = value;
            return node;
        }
        if (node.key > key) {
            node.left = doPut(node.left,key,value);
        }else {
            node.right = doPut(node.right,key,value);
        }
        updateHeight(node);
        return balance(node);
    }

????????3.7 删除节点 remove (AVLNode node)

? ? ? ? 使用递归实现删除节点思路：

? ? ? ? （1）node == null

? ? ? ? （2）没有找到 key

? ? ? ? （3）找到 key 1) 没有 2）只有一个孩子 3）有两个孩子

? ? ? ? （4）更新高度

? ? ? ? （5）balance

代码如下：

    //删除
    public AVLNode remove (int key) {
        return doRemove(root,key);
    }
    private AVLNode doRemove (AVLNode node,int key) {
        if (node == null) {
            return null;
        }
        if (node.key > key) {
            node.left = doRemove(node.left,key);
        } else if (node.key < key) {
            node.right = doRemove(node.right,key);
        }else {

            if (node.left == null && node.right == null) {
                return null;
            } else if (node.right == null) {
                node = node.left;
            } else if (node.left == null) {
                node = node.right;
            }else {
                AVLNode p = node.right;
                while (p.left != null) {
                    p = p.left;
                }
                p.right = doRemove(node.right,p.key);
                p.left = node.left;
                node = p;
            }
        }
        updateHeight(node);
        return balance(node);
    }

? ? ? ? 4.0 实现 AVLTree 核心方法的完整代码

public class AVLTree {

    AVLNode root = null;

    static class AVLNode {
        int key;
        Object value;
        AVLNode left;
        AVLNode right;
        int height = 1;

        public AVLNode(int key, Object value) {
            this.key = key;
            this.value = value;
        }

        public AVLNode(int key, Object value, AVLNode left, AVLNode right) {
            this.key = key;
            this.value = value;
            this.left = left;
            this.right = right;
        }
    }


    //获取当前节点的高度
    private int height (AVLNode node) {
        return node == null ? 0 : node.height;
    }

    //更新当前的高度
    private void updateHeight (AVLNode node) {
        node.height = Integer.max(height(node.left),height(node.right)) + 1;
    }

    //平衡因子
    private int bf (AVLNode node) {
        return  height(node.left) - height(node.right);
    }

    //左旋
    private AVLNode leftRotate (AVLNode node) {
        AVLNode r = node.right;
        node.right = r.left;
        r.left = node;
        updateHeight(node);
        updateHeight(r);
        return r;
    }

    //右旋
    private AVLNode rightRotate (AVLNode node) {
        AVLNode l = node.left;
        node.left = l.right;
        l.right = node;
        updateHeight(node);
        updateHeight(l);
        return l;
    }

    //左右旋
    private AVLNode leftRightRotate (AVLNode node) {
        AVLNode l = node.left;
        node.left = leftRotate(l);
        return rightRotate(node);
    }

    //右左旋
    private AVLNode rightLeftRotate (AVLNode node) {
        AVLNode r = node.right;
        node.right = rightRotate(r);
        return leftRotate(node);
    }

    //检查节点是否失衡，重新平衡代码
    private AVLNode balance (AVLNode node) {
        if(node == null) {
            return  null;
        }
        if (bf(node) > 1 && bf(node.left) >= 0) {
            return rightRotate(node);
        } else if (bf(node) > 1 && bf(node.left) < 0) {
            return leftRightRotate(node);

        } else if (bf(node) < -1 && bf(node.right) <= 0) {
            return leftRotate(node);

        }else if (bf(node) < -1 && bf(node.right) > 0) {
            return rightLeftRotate(node);
        }
        return node;
    }

    //更新
    public AVLNode put (int key, Object value) {
        return doPut(root,key,value);
    }

    private AVLNode doPut(AVLNode node, int key, Object value) {
        if (node == null) {
            return new AVLNode(key,value);
        }
        if (node.key == key) {
            node.value = value;
            return node;
        }
        if (node.key > key) {
            node.left = doPut(node.left,key,value);
        }else {
            node.right = doPut(node.right,key,value);
        }
        updateHeight(node);
        return balance(node);
    }

    //删除
    public AVLNode remove (int key) {
        return doRemove(root,key);
    }
    private AVLNode doRemove (AVLNode node,int key) {
        if (node == null) {
            return null;
        }
        if (node.key > key) {
            node.left = doRemove(node.left,key);
        } else if (node.key < key) {
            node.right = doRemove(node.right,key);
        }else {

            if (node.left == null && node.right == null) {
                return null;
            } else if (node.right == null) {
                node = node.left;
            } else if (node.left == null) {
                node = node.right;
            }else {
                AVLNode p = node.right;
                while (p.left != null) {
                    p = p.left;
                }
                p.right = doRemove(node.right,p.key);
                p.left = node.left;
                node = p;
            }
        }
        updateHeight(node);
        return balance(node);
    }
}

?