动手实现双线性插值

双线行插值其实是做了三次单线性插值

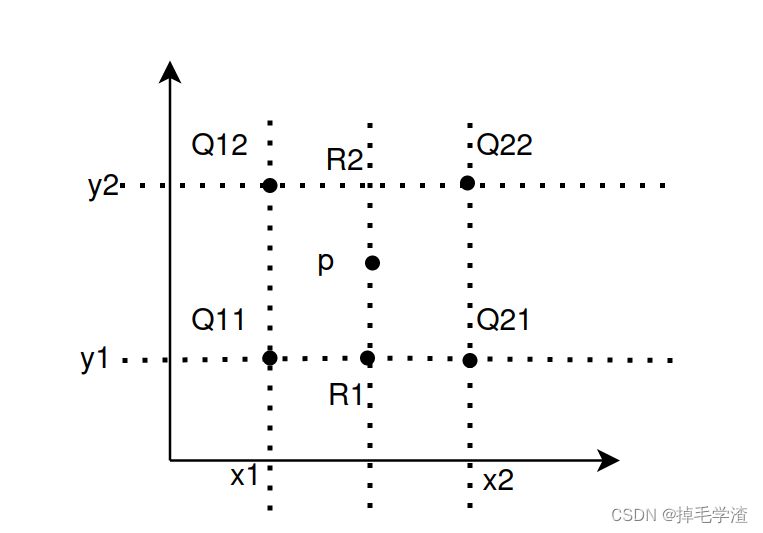
如上图所示，在计算插值点p的像素值的时候，先是通过两次单线性插值得到$R_1$和$R_2$，然后单次插值得到p的值，公式如下所示（公式由单线性插值得到）：
$$f(R_1)=\frac{x_2?x}{x_2?x_1}f(Q_{11})+\frac{x?x_1}{x_2?x_1}f(Q_{21})$$
$$f(R_2)=\frac{x_2?x}{x_2?x_1}f(Q_{12})+\frac{x?x_1}{x_2?x_1}f(Q_{22})$$
$$f(p)=\frac{y_2?y}{y_2?y_1}f(R_1)+\frac{y?y_1}{y_2?y_1}f(R_2)$$

将$f(R_1)$和$f(R_2)$代入得：
$$f(p)=\frac{(x_2?x)(y_2?y)}{(y_2?y_1)(x_2?x_1)}f(Q_{11})+\frac{(x?x_1)(y_2?y)}{(y_2?y_1)(x_2?x_1)}f(Q_{21})+\frac{(x_2?x)(y?y_1)}{(y_2?y_1)(x_2?x_1)}f(Q_{12})+\frac{(x?x_1)(y?y_1)}{(y_2?y_1)(x_2?x_1)}f(Q_{22})$$

由于是邻近点，所以有$x_2?x_1=1$、$y_2?y_1=1$，因此上式可以简化为：

$f(p)=(x_2?x)(y_2?y)f(Q_{11})+(x?x_1)(y_2?y)f(Q_{21})+(x_2?x)(y?y_1)f(Q_{12})+(x?x_1)(y?y_1)f(Q_{22})$

令$x=x_1+u$、$y=y_1+v$，因此上述等式可以再次简化为：
$f(p)=(1?u)(1?v)f(Q_{11})+u(1?v)f(Q_{21})+v(1?u)f(Q_{12})+uvf(Q_{12})$

程序如下：

import numpy as np
import matplotlib.pyplot as plt
import cv2

def bilinear_interpolation(image,ratio):
    h,w,_=image.shape
    dst_h,dst_w=int(h*ratio),int(w*ratio)
    dst=np.zeros([dst_h,dst_w,3])
    for dst_y in range(dst_h):
        for dst_x in range(dst_w):
            # find the position in the src_image
            src_x=dst_x/ratio
            src_y=dst_y/ratio

            i=int(np.floor(src_x))
            j=int(np.floor(src_y))

            u=src_x-i
            v=src_y-j

            if i==w-1:
                i=w-2
            if j==h-1:
                j=h-2
            dst[dst_y,dst_x]=(1-u)*(1-v)*image[j,i]+u*(1-v)*image[j+1,i]+v*(1-u)*image[j+1,i+1]+u*v*image[j+1,i]
    return dst

if __name__=="__main__":
    image=cv2.imread("cat1.png")
    dst_image=bilinear_interpolation(image,2)
    cv2.imwrite("./dst_image.png",dst_image)