离散数学学习要点——命题逻辑

数理逻辑

命题逻辑

命题

判断一句话是否是命题有两个关键

• 1、是陈述句
• 2、有且只有一个真值

---

• 2是个素数
• • 是命题
• x + y < 5
• • 不是命题，是命题函数
• 我正在说谎
• • 不是命题，是悖论（从它的真可以判断它的假，从它的假又可以判断他的真。）。如果真值为T，那么他就正在说谎话，“我在说谎”这句话就是假的；若真值为F，那么他就没有说谎，“我正在说谎”这句话就是真的。

命题的种类

原子命题（简单命题）

• 不能再分解成更简单陈述句的命题

---

复合命题（分子命题）

• 由若干个连接词、标点符号及原子命题符合构成的命题

命题的表示

简单命题用大写字母表示，例如：

• P：今天下雨
• Q₁：小王是大学生

---

复合命题则由若干个连接词、标点符号及原子命题复合构成的命题。

逻辑连接词

复合命题用“逻辑联结词”将原子命题联结起来表达
归纳自然语言中的联结词，定义了六个逻辑联结词，分别是：

否定联结词?

表示：“并非···”，“不···”等
用于对一个命题P的否定，写成“?P”，并读成“非P”。

---

定义：

• 设P为一命题，P的否定是一个新命题，记为?P。?P的真值与P的真值相反。

合取联结词∧

表示：“并且”、“不但…而且…”、“即…又…”、“尽管…还…”等。

相当于“&”

---

例：

• P：小王能唱歌
• Q：小王能跳舞
• P∧Q：小王能歌善舞

---

定义：

• 两个命题P和Q的合取是一个复合命题，记作P∧Q。当且仅当P和Q的真值均为T时，P∧Q的真值为T，其他情况下，P∧Q真值均为F。

析取联结词∨

联结词“或者”的表达分为两种情况：

• 可兼取的或，即两件事情可以同时发生。用析取**“∨”**表达。
• 不可兼取的或，即两件事情不能同时发生。用异或（也称排斥或）表达。（符号如下所示）

或

例：

• P：小王能唱歌
• Q：小王能跳舞
• P∨Q：小王能唱歌或者能跳舞
  小王能唱歌与能跳舞可以同时发生，我们用析取”∨“表达

---

定义：

• 两个命题P和Q的析取是一个复合命题，记作P∨Q。当且仅当P和Q的真值均为F时，P∨Q的真值为F，其他情况下，P∨Q的真值均为T。

异或

当且仅当P与Q的真值相同时，P异或Q的真值为F，真值不同时为T

条件?

表示“如果…那么…”，“若…则…”等。

---

例：

• P：土壤缺少水分
• Q：这颗植物会死亡
• P?Q：如果土壤缺少水分，这颗植物就会死亡。

---

P?Q读成“若P则Q”。
称P是P?Q的前件，Q是P?Q的后件。也可以说P是Q的充分条件，Q是P的必要条件

---

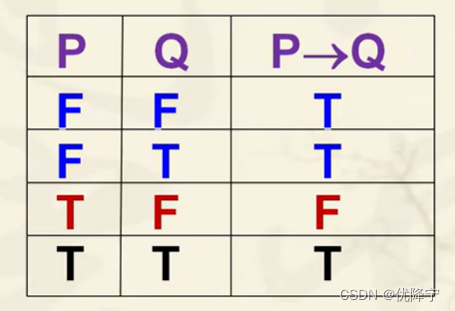
• 当且仅当P为T，Q为F时，P?Q的真值为F；在其他指派下，P?Q的真值均为T。
• 用“?”表达必须前件是后件的充分条件，即若前件成立，后件一定成立。

注意哪个是前件，哪个是后件！

等价（双条件）联结词?

表示“当且仅当”、“充分必要”等。

---

定义

• 当且仅当P与Q的真值相同时，P?Q的真值为T，否则为F。

maybe同或

联结词真值表

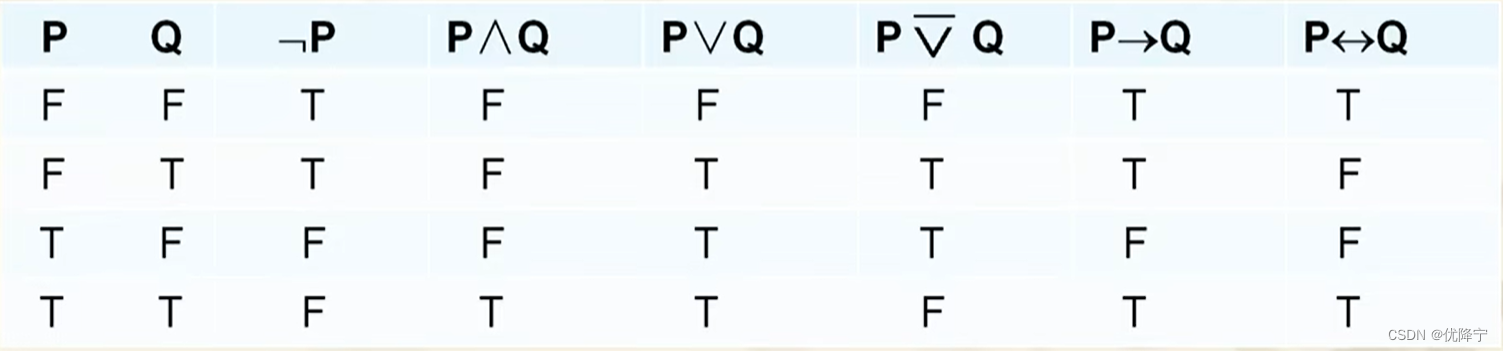
命题逻辑中的命题的符号化

命题符号化，就是将自然语言表达的句子用符号化的命题公式来表达。

---

命题符号化的步骤：

• 1、先将语句分解成原子命题。
• 2、将每个原子命题用大写祖母表示。注意每个原子命题都必须是一个完整的句子。
• 3、用确切的逻辑联结词联结原子命题，构成给定命题的符号表达式。

命题公式及其真值表

命题公式

在命题公式中有三种数据类型:

• 命题常项：即命题的真值
• 常值命题：即具体命题
• 命题变元：用大写字母表示的任一命题。命题变元本身不是命题，因为它没有固定真值，只有给它赋值，才变成命题。

将一个命题常项或常值命题赋予命题变元的过程称为给命题变元赋值，也称为对命题变元作指派

---

合式公式（合法的命题公式）定义：

• 1、单个命题变元、常值命题及命题常项是合式公式。
• 2、若A是合式公式，则?A是合式公式。
• 3、若A和B都是合式公式，则（A∧B），（A∨B），（A?B），（A?B）都是合式公式。
• 4、当且仅当有限次地应用1、2、3所得到地符号串是合式公式

---

为了简化命题公式，约定：

• 1、最外层括号可省
• 2、不影响运算次序地括号可省
  运算次序由高到底为：?，∨，∧，?，?

真值表

定义:

• 一个含有命题变元的命题公式不是命题，因为它没有固定真值，但是给其中的所有命题变元赋值以后它就有了唯一的真值。将所有各种赋值情况汇列成表，即为该命题公式地真值表

---

构造真值表的步骤

• 由于每个命题变元都有两种赋值可能性（T，F），所以含有n（n≥1）个命题变元的命题公式真值表有2ⁿ行。
• 将n个命题变元按字母次序排列
• 将F记为0，T记为1，按照二进制的次序赋值。
• 赋值从00…0开始,然后按二进制加法依次加1，直到11…1为止。
• 对每个赋值，计算命题公式的真值。

命题公式的等价

---

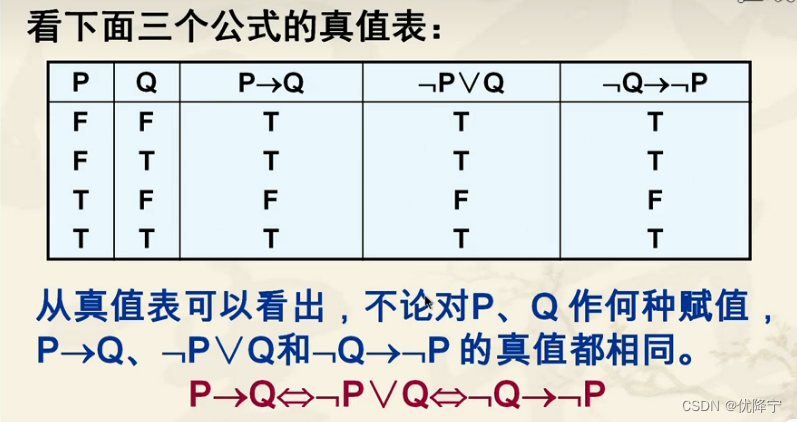
定义：

• A、B是含有命题变元P₁、P₂、…，P_n的命题公式，如不论对P₁，P₂，…P_n作何种赋值，A和B的真值均相同，则称命题公式A与B等价，记作A?B
• 若两个命题公式的真值表相同，则它们等价。

---

基础等价公式

---

等价公式的证明方法

• 方法一：列真值表
• 方法二：用等价公式变换。（用置换定律）

置换定律：A是一个命题公式，X是A中的一部分且也是合式公式，如果X?Y，用Y代替A中的X得到公式B，则A?B。

---

对偶式

• 在一个只含有联结词?，∨，∧的公式A中，将∨换成∧，将∧换成∨，T换成F，F换成T，其余部分不变，得到另一个公式A^*，称A与A^*互为对偶式
  
  

---

等价的性质：

• 1、有自反性：对任何命题公式A，均有A?A。
• 2、有对称性：若A?B，则有B?A。
• 3、有传递性：若A?B且B?C，则有A?C。

重言式与重言蕴含式

重言式

• ?P∨P为重言式（永真式）
• ?P∧P为矛盾式（永假式）

---

重言式定义

• 若公式A?T，则A为重言式或永真式
• 若公式A?F，则A为矛盾式或永假式

重言蕴含式

定义

• 当且仅当A?B是重言式，则称A重言（永真）蕴含B，记作A?B
• 即 若A?B?T，则A?B

---

证明A?B

• 假设前件A为真，若在此假设下能推出后件B也为真，则A?B成立
• 假设后件B为假，若在此假设下能推出前件A也为假，则A?B成立。

---

基础重言

---

重言蕴含的性质

• 1、有自反性：对任何命题公式A，有A?A。
• 2、有传递性：若A?B且B?C，则A?C。
• 3、有反对称性：若A?B且B?A,则A?B
• 4、若A?B且A?C，则A?B∧C。

析取范式与合取范式

析取范式

定义

• 命题公式A如果可等价地写成如下形式：A₁∨A₂∨…∨A_n（n≥1）
• 其中每个项A_i（i=1，2…，n）是命题变元或其他否定形式的合取式，称该公式为A的析取范式。

合取范式

定义

• 命题公式A如果可等价地写成如下形式：A₁∧A₂∧…∧A_n（n≥1）
• 其中每个项A_i（i=1，2…，n）是命题变元或其否定形式地析取式，称该公式为A的合取范式

析取范式与合取范式的写法

1、用去掉“?”和“?”
2、将“?”移到命题变元前。
用对偶式
3、用分配律、幂等律等公式进行整理，使之成为所要求的形式。

主析取范式

小项定义

• 是n个命题变元的合取式，其中每个变元必出现且仅出现一次（以本身或否定形式），称这个合取式为小项
• 若有n个变元，则由有2ⁿ个小项

含有两个变元的小项只有以下情况

---

小项编码

• 含有n个变元的小项的角标用n位二进制码表示。
• 变元按字母次序排列
• 用1表示变元本身，0表示变元的否定形式。
  

---

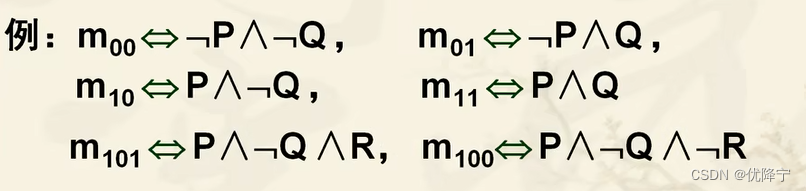
规律：

• 每个小项当且仅当其赋值与编码相同时，其真值为T；而其余2ⁿ-1组赋值均使该小项的真值为F。
• 全体小项的析取式为永真式，记为：∑m_i ?m₀∨m₁∨…∨m_2^n^-1?T

---

主析取范式定义

• 若一个命题公式的析取范式为A₁∨A₂∨…∨A_n（n≥1），其中每个A_i（i=1，2，…，n）都是小项，则称之为该命题公式的主析取范式。

---

主析取范式的求法

• 1、先写出给定公式的析取范式：A₁∨A₂∨…∨A_n
• 2、为使每个A_i都变成小项，对缺少变元的项。A_i要补全变元，比如缺变元R，就用“∧（R∨?R）”的形式补R。
• 3、用分配律等公式加以整理

---

求主析取范式的真值表法

• 1、列出给定公式的真值表
• 2、找出该公式真值表中每个为“T”行的赋值所对应的小项
• 3、用“∨”联结上述小项，即可。
  

---

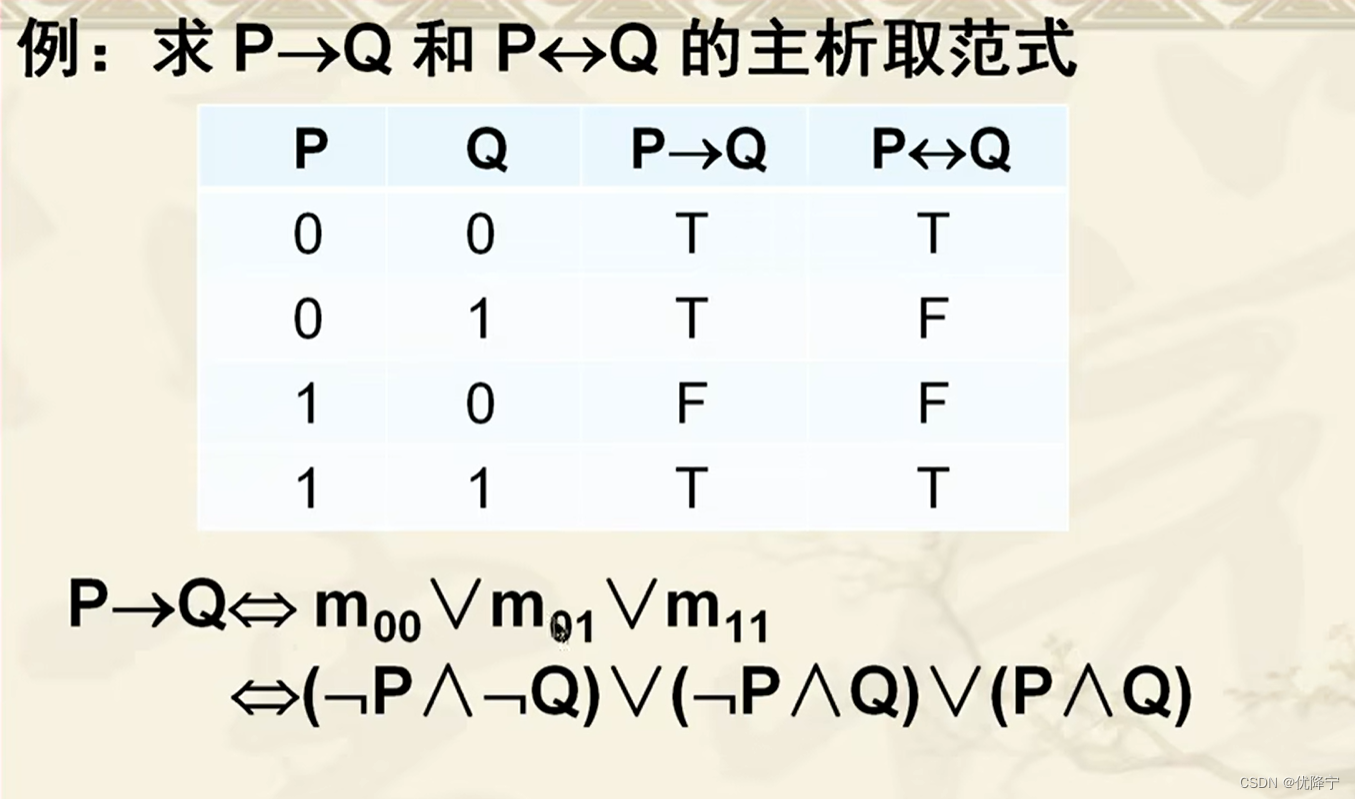
定理

• 在真值表中，一个使公式的真值为T的赋值所对应的小项的析取，即为此公式的主析取范式。

---

思考

• 那永真式的主析取范式呢？所有小项的析取。

主合取范式

大项定义

• 主合取范式是n个命题变元的析取式，其中每个变元必出现且仅出现一次（以本身或否定形式），称该析取式为大项
• 有n个变元，则有2ⁿ个大项。

---

大项的编码

• 大项的编码正好与小项相反。用0表示变元本身，1表示变元的否定形式。

如何记忆：析取是11出1，合取是00出0，这是两者的唯一出1和0的情况。

---

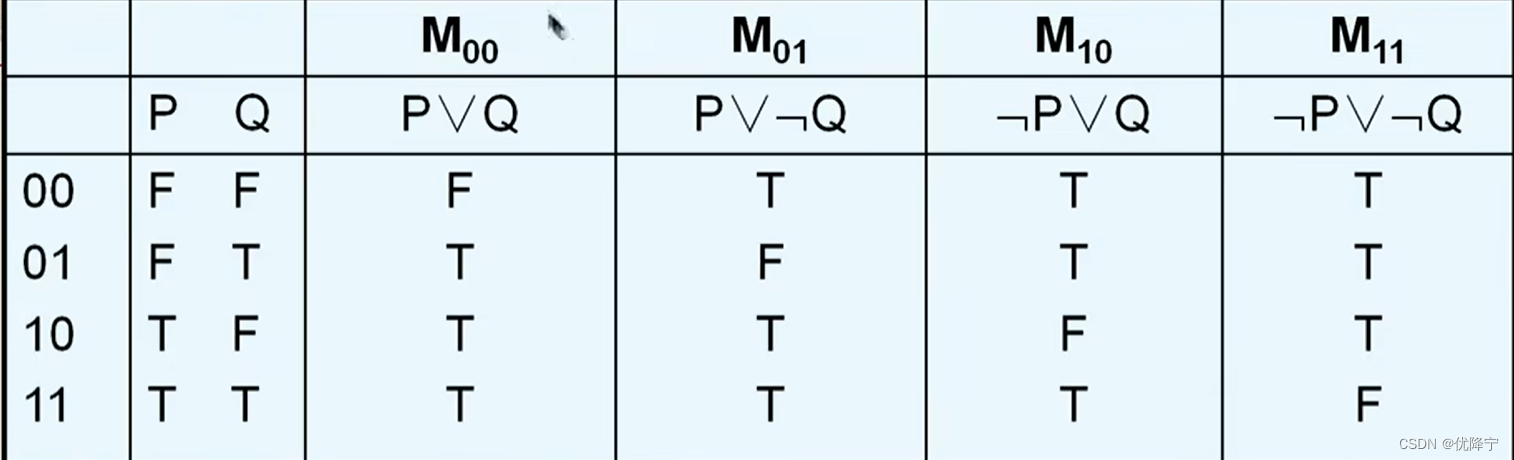
• 每个大项当且仅当其赋值与编码相同时，其真值为F
• 其余2^n-1组赋值均使该大项的真值为T。
• 全体大项的合取式必为永假式。
  

---

主合取范式定义

• 若一个命题公式的合取范式为A₁∧A₂∧…∧A_n（n≥1），其中每个A_i（i=1，2，…，n）都是大项，则称之为命题公式的主合取范式。

---

求主合取范式的步骤

• 先写出给定公式的合取范式A₁∧A₂∧…∧A_n。
• 为了使每个A_i变成大项，对缺少变元的项A_i补全变元，比如缺变元R，用“∨（R∧?R）”的形式补R
• 3、用分配率等公式加以整理
  

---

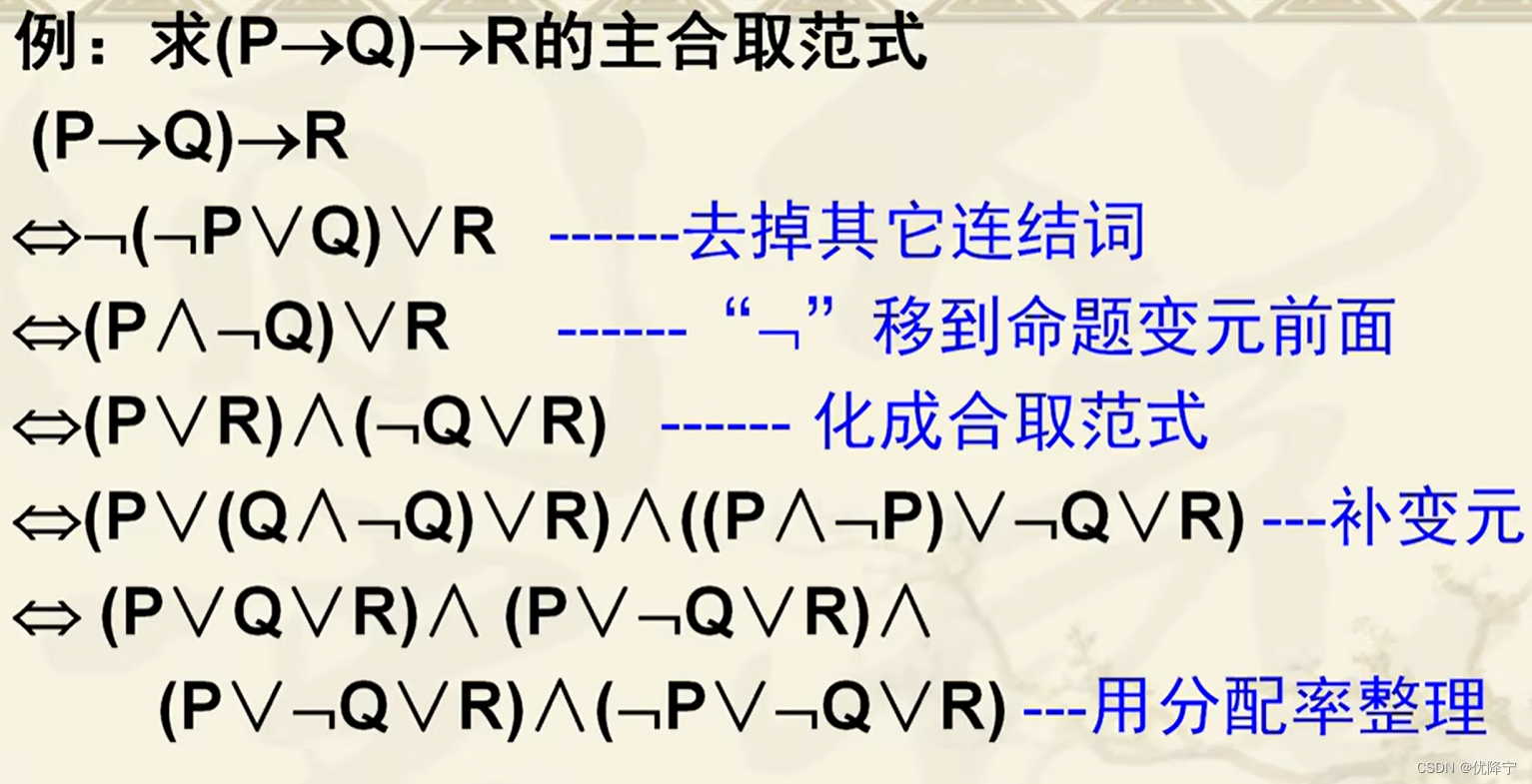
主合取范式的真值表求法

• 1、列出给定公式的真值表
• 2、找出该公式真值表中的每个为“F”行的赋值所对应的大项。
• 3、用“∧”联结上述大项，即可。

---

定理

• 在真值表中，一个使公式的真值为F的赋值所对应的大项的析取，即为此公式的主合取范式。

命题逻辑推理

直接推理

• 推理的过程就是证明永真蕴含式的过程。

---

令H₁，H₂，…，H_n是已知的命题公式（前提）
若有H₁∧H₂∧…∧H_n?C
则称C是H₁，H₂，…，H_n的有效结论，简称结论

---

两个推理规则

• P规则（引入前提规则）：在推理过程中，可以随时引入前提。
• T规则（引入结论规则）：在推理过程中，如果前面有一个或几个公式重言蕴含公式S，则可将S纳入推理过程中。

---

推理方法

• 直接推理
• 间接推理
• • 条件论证
• • 反证法

---

---

推理格式

• 第一列为步骤号
• 第二列为给定前提或得出的结论
• 第三列为注释列，标明是前提还是得到的结论，以及此结论是从哪几步得到的，所用公式得类型。
  

间接推理

CP规则：
如果要证明的结论是R?S的形式，则可以把结论中R?S的前件R作为附加前提，与给定的前提一起推出后件S即可。

---

定义：

• 设H₁，H₂，…，H_n是命题公式，P₁，P₂，…，P_m是公式中的命题变元。如果对P₁，P₂，…，P_m，至少有一组赋值使得H₁∧H₂∧…∧H_n的真值为T，则称公式集合{H₁，H₂，…，H_n}是相容的（也称是一致的）
• 如果对P₁，P₂，…，P_m的每一组赋值，都使得H₁∧H₂∧…∧H_n的真值为F，则称公式集合{H₁，H₂，…，H_n}是不相容的（也称是不一致的）

---

反证法：

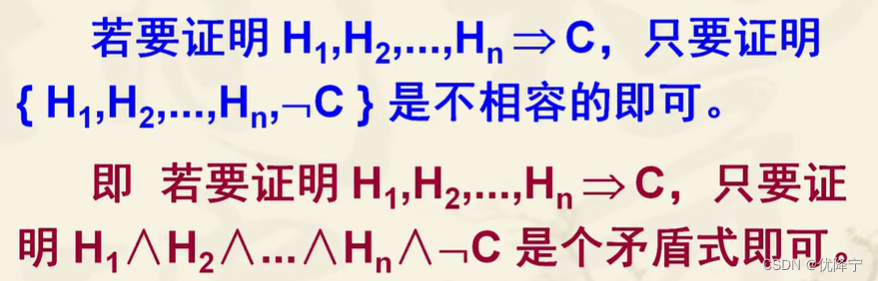
谓词逻辑

谓词逻辑的基本概念

谓词的出现

问题提出：

• 所有的金属都导电，铜是金属，所以铜导电。
  设：
• A：所有的金属都导电
• B：铜是金属
• C：铜导电
• 该推理符号化为：A，B?C

这是著名的三段论推理，A是大前提，B是小前提，C是结论。显然，这个推理是有效的，但是这个推理用命题逻辑是无法推证的。

---

Why

• 因为命题A、B、C在句子内部是有联系的，而且把命题表示成一个大写字母，就掩盖了这种联系。也就是说一个命题仅用一个大写字母表示的方式太粗了，我们必须加以细化，用另外的表示方式来表达命题。
• 命题是表达判断的陈述句，将其细分，表达出主语、谓语及宾语（若有的话），而一个句子中“谓语”最重要，这就提出了谓词的概念。

---

相关的基本概念

个体

个体

• 能够独立存在的具体或抽象的事物，称之为个体，也称之为客体。通常用小写英文字母a、b、c、…表示。
• 例如：小张、小李、8、a、沈阳、社会主义等等都是客体。

---

个体常项

• 具体的或特定的个体。
• 常用a、b、c、…等小写字母表示

---

个体变元

• 泛指某一个个体
• 常用x，y，z，…等小写字母表示

谓词

• 用以刻化个体属性或者表达个体之间关系的词，即为谓词。

• 谓词用大写字母表示
  
  

• 一个命题若其中个体的个体常项，则该命题用谓词后边加括号，括号内是若干个体表示

---

• 谓词也有常项和变项之分。
• 表示具体性质与关系的谓词称为谓词常项。
• 表示某一性质或关系的谓词称为谓词变项。
• 一般地，含有n（n>0）个个体变元x₁，x₂，…，x_n的谓词P称为n元谓词，记作P（x₁，x₂，…，x_n）。
• 当n = 1，P（x）表示x具有性质P

---

约定

• 将不带个体变元的谓词称为0元谓词。例如：S（a），G（3，7）
• 当谓词是常项时，0元谓词是命题；
• 否则当谓词是变项时，0元谓词是命题变元。

命题函数

• 含有n个变元的命题函数是以个体域为定义域，以{F，T}为值域的n元函数。
  注意：命题函数本身并不是命题，只有在括号内填入足够的具体客体，或用足够的量词约束后才变成命题。

B(x,y,z)：x在y与z之间，是命题函数，不是命题
c：锦州，d：沈阳，e：山海关
B（c，d，e）表示：锦州在沈阳与山海关之间，是命题。

个体域

• 个体变元的取值范围，称之为个体域，也称之为论域。
• 由所有个体构成的个体域，称之为全总个体域，他是“最大”的个体域
• 对于一个命题函数，如果没有指明其个体域，则假定其个体域是全总个体域

量词

• 在命题中，表示对个体量化的词，称之为量词。

---

• 存在量词：记作?，存在
• 全称量词：记作?，任意

---

• 量词的指导变元：量词后边要有一个个体变元，指明对那个个体变元进行量化，称此个体变元是指导变元。
  ?x，?x，其中x就是指导变元

---

特性谓词

• 一般来说，特性谓词是描述个体特征的谓词，往往就是给定命题中量词后边的那个名词。
  ———————
  特性谓词的添加规则
• 对全称量词，特性量词常作蕴含前件。
• 对存在量词，特性谓词常作合取项。

谓词公式及变元的辖域

原子谓词公式

• 称n元谓词P（x₁，x₂，…，x_n）为原子谓词公式
• 例如P，Q，A（x，y），B（x，y，a）都是原子谓词公式

谓词合式公式

1. 原子谓词公式是合式公式
2. 如果A是合式公式，则?A也是合式公式。
3. 如果A、B是合式公式，则（A∧B）、（A∨B）、（A?B）、（A?B）都是合式公式
4. 如果A是合式公式，x是A中的个体变元，则?xA和?xA也是合式公式
5. 只有有限次地应用1~4得到的符号串才是合式公式

量词的作用域（辖域）

• 在谓词公式中，量词的作用范围称之为量词的作用域，也叫量词的辖域。
  

---

• 如果量词后边只是一个原子谓词公式时，该量词的辖域就是此原子谓词公式。
• 如果量词后边是括号，则此括号所表示的区域就是该量词的辖域
• 如果多个量词紧挨着出现，则后边的量词及其辖域就是前边量词的辖域

自由变元与约束变元

• 在谓词公式中的个体变元可以分成两种，一种时受到量词约束的，一种是不受量词约束的

---

定义

• 如果客体变元x在?x或者?x的辖域内，则称x在此辖域内约束出现，并称x在此辖域内是约束变元。否则x是自由出现，并称x是自由变元
  

说明

1. 一个n元谓词P（x₁，x₂，…，x_n），若在前边添加k个量词，使其中的k个个体变元变成约束变元，则此n元谓词就变成了n-k元谓词
2. 一个谓词公式如果无自由变元，他就表示一个命题
   

变元换名

原因
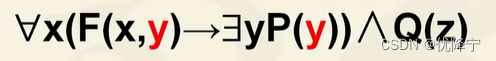- y既是自由变元，也是约束变元。为避免混淆，需要对约束变元换名

---

约束变元换名规则

• 设A为一谓词公式，将A中某量词辖域内的一个约束变元的所有出现及相应的指导变元全部改成A中没出现过的某个变元符号，A中其余部分不变，记所得公式A‘，则A?A’
  

---

自由变元代入规则

• 设A为一谓词公式，将A中某个自由出现的个体变元的所有出现用某个A中没出现过的变元符号代替，A中其余部分不变，即所得公式为A‘，则A?A’

谓词逻辑中的命题符号化

• 命题符号化表达式与个体域有关系。而个体域的指定需随题目而定。能指定个体域的当然要指定，这样会使表达式变得简单。若不指定个体域，则为全总个体域

---

最基本的命题符号化

1. 主语是具体个体对象的，用谓词加括号，括号里是具体个体表示。
2. 描述所有的、任意的个体对象，用全称量词，特性谓词作为蕴含前件
3. 描述一些客体对象，用存在量词，特性谓词作合取项
   

---

• 在有些命题中，某些个体对象的量词没有明确给出，要仔细分析并写出这些隐含量词。
• 命题的符号表达式中所有个体变元必须都是约束变元，才表示命题。即在命题的符号表达式中，一定没有自由变元

谓词演算的等价式与蕴含式

对谓词公式赋值

1. 指定非空个体域
2. 将谓词公式中的命题变元，用确定的命题替代
3. 对公式中的个体变元用论域中的具体个体替代
4. 对公式中含有的谓词变项，用谓词常项替代

谓词公式的永真式

• 给定谓词公式A，如果不论对其作任何赋值，都使得谓词公式A的真值为真，则称A为永真式

谓词公式的等价公式

• 给定谓词公式A、B，如果A?B是永真式，则称A与B等价，记作A?B。

谓词公式的永真蕴含式

• 给定谓词公式A、B，如果A?B为永真式，则称A永真蕴含B，记作A?B。

谓词演算的等价式与蕴含式

由命题演算推广出的公式

• 因一个不含自由变元的谓词公式是命题。而含有n个自由变元的原子谓词公式，可以看成是命题变元。所以只要不牵涉到量词的运算，命题演算中的等价公式和重言蕴含公式均可推广到谓词演算中使用。

有限个体域消去量词的等价公式