二叉树的应用

• 前言

????????在前面文章中我为大家介绍了树形结构的基本概念，又重点介绍了树形结构中的二叉树，讲解了二叉树的概念，性质，还有一些基本操作，然而二叉树的内容还不仅如此，二叉树是一种较为复杂的数据结构，在知道二叉树的一些知识前提下看看我们能不能将二叉树应用起来，解决二叉树的相关问题呢？

问题1：二叉树的构建及遍历

（1）问题介绍

????????编一个程序，读入用户输入的一串先序遍历字符串，根据此字符串建立一个二叉树（以指针方式存储）。 例如如下的先序遍历字符串： ABC##DE#G##F### 其中“#”表示的是空格，空格字符代表空树。建立起此二叉树以后，再对二叉树进行中序遍历，输出遍历结果。

（2）解题思路

? ? ? ? 二叉树的相关问题，大部分都用到了递归思想，在进行二叉树的遍历过程中我们采用了递归的思想，所以创建时我们依然采用递归的思想，首先我们定义一个成员变量i用来遍历输入的字符串，使用create作为二叉树创建的方法名，create方法返回值就是树中结点的类型，在create方法中定义一个结点root为null，当遍历字符为‘#’时i自增，返回root，如果字符不为‘#’，就将字符赋给root的数据域，然后进行在调用create方法对root的左子树与右子树进行创建，最后调用中序遍历对创建的二叉树进行遍历验证。

（3）代码实现

? ? ? ? 问题的实现代码如下，更多详细解释在代码注释中。

import java.util.Scanner;

//树中结点类型
class TreeNode{
    char val;
    TreeNode left;
    TreeNode right;

    public TreeNode(char val){
        this.val = val;
    }
}

//主类,进行方法定义与程序的运行
public class Main {
    //成员变量i,用来记录所遍历字符串中字符的位置
    static int i = 0;
    public static void main(String[] args) {
        //创建Scanner对象,从键盘输入
        Scanner in = new Scanner(System.in);
        //创建String对象str,用来接收输入的字符串
        String str = in.nextLine();
        //创建结点root,接收方法createTree的返回值
        TreeNode root = createTree(str);
        //进行中序遍历,输出创建的二叉树
        inorder(root);
    }
    
    //方法createTree,根据传入的字符串创建二叉树并返回二叉树的根结点
    public static TreeNode createTree(String str){
        //创建一个结点root
        TreeNode root = null;
        if(str.charAt(i) != '#'){
            //将当前字符赋给root的数据域
            root = new TreeNode(str.charAt(i));
            //i自增,用来遍历下一个字符
            i++;
            //创建root的左子树
            root.left = createTree(str);
            //创建root的右子树
            root.right = createTree(str);
        }else{
            //当前字符为'#'代表当前创建树为空树
            i++;
        }
        //返回创建树的根结点
        return root;
    }

    //中序遍历
    public static void inorder(TreeNode root){
        if(root == null){
            return;
        }
        inorder(root.left);
        System.out.print(root.val + " ");
        inorder(root.right);
    }
}

问题2：判断平衡二叉树

（1）问题介绍

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点?的左右两个子树的高度差的绝对值不超过 1 。

（2）解题思路

? ? ? ? 平衡二叉树的每棵子树也都应该是平衡二叉树，所以我们利用递归，递到叶子结点再进行归，这样可以边求子树高度又可以对每棵子树进行判断，只要有一棵子树不是平衡二叉树那这棵树就不是平衡二叉树。

（3）代码实现

????????问题的实现代码如下，更多详细解释在代码注释中。

class Solution {
    public boolean isBalanced(TreeNode root) {
        //空树也是平衡二叉树
        if(root == null){
            return true;
        }
        //树不是空树,利用方法judge来判断树是否为平衡二叉树
        return judge(root) >= 0;
    }
    //方法judge用来判断平衡二叉树和求树的高度,返回-1代表不是平衡二叉树
    public int judge (TreeNode root){
        //当root为null,此树高度为0
        if(root == null){
            return 0;
        }
        //判断左子树是不是平衡二叉树并求左子树的高度
        int judgeLeft = judge(root.left);
        //返回值小于0,说明左子树不是平衡二叉树,直接返回不用继续判断
        if(judgeLeft <0){
            return -1;
        }
        //判断右子树是不是平衡二叉树并求右子树的高度
        int judgeRight = judge(root.right);
        //Math.abs方法用来求两数差的绝对值,当两树高度差小于1说明是平衡二叉树
        if(judgeLeft>=0 && judgeRight>=0 && Math.abs(judgeLeft - judgeRight)<=1){
            //返回值为树的高度
            return judgeLeft>judgeRight ? (judgeLeft+1) : (judgeRight+1);
        }
        //不满足上述条件说明此树不是平衡二叉树
        return -1;
    }
}

问题3：另一棵树的子树

（1）问题介绍

????????给你两棵二叉树?root?和?subRoot?。检验?root?中是否包含和?subRoot?具有相同结构和节点值的子树。如果存在，返回?true?；否则，返回?false?。

????????二叉树?tree?的一棵子树包括?tree?的某个节点和这个节点的所有后代节点。tree?也可以看做它自身的一棵子树。

（2）解题思路

? ? ? ? 如果两棵树相等，那么也满足这棵树是另一棵树的子树，所以我们可以将问题转化为判断两棵树是否相等，利用递归的思想，对root进行递归，只要root中有一棵子树与subRoot相等就说明subRoot是root的子树。如何判断两棵树是否相等，可以对两棵树同时进行遍历，边遍历边进行比较。

（3）代码实现

????????问题的实现代码如下，更多详细解释在代码注释中。

class Solution {
    //判断subRoot是不是root的子树
    public boolean isSubtree(TreeNode root, TreeNode subRoot) {
        //两棵树相同返回真
        if (isSameTree(root,subRoot)){
            return true;
        }
        //上面if语句已经包含判断root与subRoot都为null的情况了
        //所以这里当root为null时subRoot一定不为null,停止递归,返回假
        if(root == null){
            return false;
        }
        //递归判断root的左子树与右子树,看看有没有与subRoot相同的树,有就返回真
        return isSubtree(root.left,subRoot) || isSubtree(root.right,subRoot);
    }
    //判断p与q两棵树相吧相同
    public boolean isSameTree(TreeNode p, TreeNode q) {
        //如果两棵树都是空树那么他们相同
        if (p == null && q == null){
            return true;
        }else if (p == null || q == null){
            //当一棵树为空一棵树不为空,他们不相同
            return false;
        }
        //判断当前根结点值是否相同
        if(p.val == q.val){
            //根结点值相同,递归判断他们左子树,右子树是否相同,
            //只有都相同才代表两棵树相同
            return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);
        }
        //执行到这说明两棵树不相同返回false
        return false;
    }
}

问题4：对称二叉树

（1）问题介绍

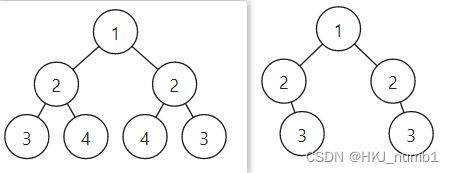
????????给你一个二叉树的根节点?root?， 检查它是否轴对称。

（2）解题思路

? ? ? ? ?如果一棵二叉树为空树那么他是对称二叉树，如果他不是空树，那么他是否为对称二叉树与他的根结点无关，所以直接判断其左右子树即可，注意，左子树根结点与右子树根结点对应，左子树左孩子与右子树右孩子对应，左子树右孩子与右子树左孩子对应，对称是一个镜像关系，要注意判断时的对应关系。

（3）代码实现

????????问题的实现代码如下，更多详细解释在代码注释中。

class Solution {
    public boolean isSymmetric(TreeNode root) {
        //当树为空树或者树中只有一个结点此树为对称二叉树
        if (root == null || (root.left ==null && root.right ==null)){
            return true;
        }
        //方法isSymmetricChild返回值就是判断结果
        return isSymmetricChild(root.left,root.right);
    }
    //判断左右子树是否对称
    public boolean isSymmetricChild(TreeNode leftTree,TreeNode rightTree){
        //如果两棵树都是空树那么他们相同
        if(leftTree == null && rightTree == null){
            return true;
        }else if(leftTree == null || rightTree == null){
            //当一棵树为空一棵树不为空,他们不相同
            return false;
        }
        //当左树根结点的值与右树根结点的值不一样,说明他们不是对称的
        if(leftTree.val != rightTree.val){
            return false;
        }
        //返回左树与右树成对应关系的左右孩子是否相同的结果
        return isSymmetricChild(leftTree.left,rightTree.right)&&
                isSymmetricChild(leftTree.right,rightTree.left);
    }
}

问题5：翻转二叉树

（1）问题介绍

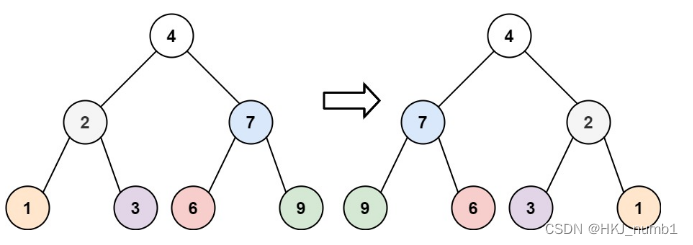
给你一棵二叉树的根节点?root?，翻转这棵二叉树，并返回其根节点。

（2）解题思路

????????由图可知，翻转二叉树就是将二叉树中每棵子树的左右子树进行交换，利用递归将每棵子树的左右子树进行交换即可解决问题。?

（3）代码实现

????????问题的实现代码如下，更多详细解释在代码注释中。

class Solution {
    public TreeNode invertTree(TreeNode root) {
        //当树为空树,不用翻转
        if(root == null){
            return root;
        }
        //当树中只有一个结点,不用翻转
        if(root.left == null && root.right == null){
            return root;
        }
        //创建结点tmp用来对左右树进行交换
        TreeNode tmp = root.left;
        root.left = root.right;
        root.right = tmp;
        //递归,对左子树进行翻转
        invertTree(root.left);
        //递归,对右子树进行翻转
        invertTree(root.right);
        //返回翻转后树的根结点
        return root;
    }
}

问题6：二叉树的层序遍历II

（1）问题介绍

给你二叉树的根节点?root?，返回其节点值?自底向上的层序遍历?。 （即按从叶子节点所在层到根节点所在的层，逐层从左向右遍历）

（2）解题思路

? ? ? ? 对于二叉树的层序遍历我们可以利用二维数组，每层结点都存在二维数组中对应的层，这里我们要求从最后一层开始遍历，所以在进行存储时我们采用头插法，具体操作还需要借助队列，首先将根结点存入队列，如果队列不为空说明树中还有结点没有存入二维数组，记录当前队列中元素个数，此时队列中的元素个数就是当前层要存放的元素个数，将队列首元素出队存入当前层，并将队列首元素左右子树根结点入队列，进行循环，最后返回二维数组的地址。

（3）代码实现

????????问题的实现代码如下，更多详细解释在代码注释中。

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;

class Solution {
    public List<List<Integer>> levelOrderBottom(TreeNode root) {
        //创建二维数组
        List<List<Integer>> ret = new ArrayList<>();
        //树为空树直接返回
        if (root == null){
            return ret;
        }
        //创建队列,用来存放树中结点
        Queue<TreeNode> queue = new LinkedList<>();
        //先将根结点入队列
        queue.offer(root);
        //队列不为空说明树中还有结点没有存入二维数组中
        while (!queue.isEmpty()){
            //size用来记录这层数组要存放元素个数
            int size = queue.size();
            //创建一维数组来存放这层元素
            List<Integer> list = new ArrayList<>();
            //size不为0说明这层元素没有存放完
            while (size != 0){
                //tmp用来接收队首元素
                TreeNode tmp = queue.poll();
                //出队,size减1
                size--;
                //将元素tmp存入数组中
                list.add(tmp.val);
                //将tmp的左右子树根结点入队列
                if (tmp.left != null){
                    queue.offer(tmp.left);
                }
                if (tmp.right != null){
                    queue.offer(tmp.right);
                }
            }
            //将一维数组头插到二维数组中,保证从最后一层开始遍历
            ret.add(0,list);
        }
        //返回二维数组起始地址
        return ret;
    }
}

问题7：二叉树前序非递归遍历

（1）问题介绍

给你二叉树的根节点?root?，利用非递归的方法返回它节点值的?前序?遍历。

（2）解题思路

? ? ? ? 在前面二叉树的实现中我们写过递归形式的前序遍历，这次我们要求用非递归的方式进行前序遍历，这里我们将前序遍历序列存放到顺序表中，在前序遍历过程中使用栈这一数据结构进行模拟递归，首先我们定义一个结点cur用来存放当前结点，只要结点不为空就将结点入栈并将结点存入顺序表中，前序遍历是以根-》左子树-》右子树的顺序，所以当前cur存储完就将cur更新为cur.left，当cur.left为空，将栈顶元素弹出，将cur更新为栈顶元素的right，这样就保证了前序遍历的顺序。

（3）代码实现

????????问题的实现代码如下，更多详细解释在代码注释中。

import java.util.ArrayList;
import java.util.List;
import java.util.Stack;

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        //创建顺序表,存储前序遍历的序列
        List<Integer> ret = new ArrayList<>();
        //如果当前树是空树,直接返回空顺序表
        if (root == null){
            return ret;
        }
        //定义结点cur指向当前结点
        TreeNode cur = root;
        //创建栈stack,用来模拟递归效果
        Stack<TreeNode> stack = new Stack<>();
        //当栈不为空或者当前结点不为空,说明前序遍历没有完成
        while (!stack.empty() || cur != null){
            //当前结点不为空,说明当前结点的左子树没有遍历完成
            while (cur != null){
                //将当前结点入栈进行保存,遍历当前结点右子树时弹出当前结点用来寻找其右子树
                stack.push(cur);
                //根据前序遍历顺序,将根结点先存入顺序表
                ret.add(cur.val);
                //当前结点对左子树进行遍历
                cur = cur.left;
            }
            //左子树遍历完成,弹出栈顶元素对栈顶元素右子树进行遍历
            cur = stack.pop().right;
        }
        //将前序遍历序列存入顺序表中,返回顺序表地址ret
        return ret;
    }
}

问题8：前序中序还原二叉树

（1）问题介绍

给定两个整数数组?preorder?和?inorder?，其中?preorder?是二叉树的先序遍历，?inorder?是同一棵树的中序遍历，请构造二叉树并返回其根节点。

（2）解题思路

? ? ? ? 根据前序遍历序列可以快速找到根结点，根据中序遍历序列可以快速找到根结点的左右子树，由此我们可以利用前序遍历序列与中序遍历序列进行结合，利用递归的思想将树中每棵子树的根结点都创建出来，在回溯时把每个结点都串在一起，我们利用preindex记录当前要找的根结点，inbegin记录中序遍历序列的开头，inend记录中序遍历序列结尾，index记录当前要找的根结点在中序遍历序列中的位置，在结合递归思想即可求解。

（3）代码实现

????????问题的实现代码如下，更多详细解释在代码注释中。

class Solution {
    //将preindex定义为成员变量,防止在回溯途中发生问题
    public int preindex = 0;
    //给前序遍历序列与中序遍历序列创建二叉树
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        //调用方法buildTreeChild返回创建二叉树的根结点
        return buildTreeChild(preorder,inorder,0,inorder.length-1);
    }
    //将树中每棵子树的根结点创建出来并在回溯途中连在一起
    public TreeNode buildTreeChild(int[] preorder, int[] inorder,int inbegin,int inend) {
        //当开始位置大于结束位置递归结束,当前树为空树
        if (inbegin > inend){
            return null;
        }
        //创建根结点root接收当前创建的根结点
        TreeNode root = new TreeNode(preorder[preindex]);
        //找到当前根结点在中序遍历序列中的位置
        int index = findpos(inorder,inbegin,inend,preorder[preindex]);
        //preindex++移动到下一个根结点的位置
        preindex++;
        //index为-1说明没有在中序遍历序列中找到当前根结点
        if (index == -1){
            return null;
        }
        //递归调用,开始创建当前根结点的左右子树
        //左子树的中序遍历序列就是中序遍历起始位置到当前根结点在中序遍历序列中位置
        root.left = buildTreeChild(preorder,inorder,inbegin,index-1);
        //右子树的中序遍历序列就是当前根结点在中序遍历序列中位置到中序遍历结束位置
        root.right = buildTreeChild(preorder,inorder,index+1,inend);
        //返回当前根结点
        return root;
    }
    //在中序遍历中寻找当前树中根结点的位置
    private int findpos(int[] inorder, int inbegin, int inend,int pos) {
        //从开始位置顺序查找根结点的位置
        for (int i = inbegin;i <= inend;i++){
            if (inorder[i] == pos){
                //找到返回根结点在中序遍历序列中的位置
                return i;
            }
        }
        //没找到返回-1
        return -1;
    }
}

（4）相关问题（中序后序还原二叉树）

给定两个整数数组?inorder?和?postorder?，其中?inorder?是二叉树的中序遍历，?postorder?是同一棵树的后序遍历，请你构造并返回这颗二叉树?。

? ? ? ? 具体的解题思路就跟本题类似，只不过后序遍历序列，需要我们从后往前寻找根结点，在创建每棵树的左右子树时也要注意这次要先创建右子树再创建左子树，就不过多介绍了，希望友友们根据本题讲解自己尝试解决这道题，这道题的代码我放在下面，做不出来可以进行参考：

class Solution {
    public int postindex = 0;
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        postindex = postorder.length-1;
        return buildTreeChild(inorder,0,inorder.length-1,postorder);
    }
    public TreeNode buildTreeChild(int[] inorder,int inbegin,int inend, int[] postorder) {
        if (inbegin > inend){
            return null;
        }
        TreeNode root = new TreeNode(postorder[postindex]);
        int index = findpos(inorder,inbegin,inend,postorder[postindex]);
        if (index == -1){
            return null;
        }
        postindex--;
        root.right = buildTreeChild(inorder,index+1,inend,postorder);
        root.left = buildTreeChild(inorder,inbegin,index-1,postorder);
        return root;
    }
    private int findpos(int[] inorder, int inbegin, int inend, int pos) {
        for (int i = inbegin;i <= inend;i++){
            if (inorder[i] == pos){
                return i;
            }
        }
        return -1;
    }
}

问题9：两个节点的最近公共祖先

（1）问题介绍

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

（2）解题思路

? ? ? ? 创建两个栈用来存放根到p和q结点的路径，如果两个栈长度不一样，将长的栈进行出栈，使两个栈长度相同，然后一起出栈，并将每次出栈的元素进行比较，如果出栈元素相同，当前出栈元素就是p和q的公共祖先。

（3）代码实现

????????问题的实现代码如下，更多详细解释在代码注释中。

import java.util.Stack;

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        //栈stackP存放root到p的路径
        Stack<TreeNode> stackP = new Stack<>();
        //获取root到p的路径,存到stackP中
        getPath(root,p,stackP);
        //栈stackQ存放root到q的路径
        Stack<TreeNode> stackQ = new Stack<>();
        //获取root到q的路径,存到stackQ中
        getPath(root,q,stackQ);
        //sizeP记录root到p路径长度
        int sizeP = stackP.size();
        //sizeQ记录root到q路径长度
        int sizeQ = stackQ.size();
        //如果两条路径长度不相等,将长的栈进行出栈,直到两条路径长度相等
        if (sizeP > sizeQ){
            int size = sizeP - sizeQ;
            while (size != 0){
                stackP.pop();
                size--;
            }
        }else {
            int size = sizeQ - sizeP;
            while (size != 0){
                stackQ.pop();
                size--;
            }
        }
        //stackP与stackQ同时进行出栈操作,直到栈顶元素相同
        while (stackP.peek() != stackQ.peek()){
            stackP.pop();
            stackQ.pop();
        }
        //此时两个栈的栈顶元素就是公共祖先
        return stackP.peek();
    }
    //获取root到node的路径,存放到stack中
    private boolean getPath(TreeNode root, TreeNode node, Stack<TreeNode> stack) {
        //root为空返回假,说明没有路
        if(root == null){
            return false;
        }
        //将root入栈
        stack.push(root);
        //观察栈顶元素是不是要找的结点,如果是就说明路径到终点
        if (stack.peek() == node){
            return true;
        }
        //flg1记录root左树有没有node
        boolean flg1 = getPath(root.left,node,stack);
        if (flg1){
            return true;
        }
        //flg2记录root右树有没有node
        boolean flg2 = getPath(root.right,node,stack);
        if (flg2){
            return true;
        }
        //当前左右都不是node,将栈顶元素弹出
        stack.pop();
        return false;
    }
}

问题10：根据二叉树创建字符串

（1）问题介绍

给你二叉树的根节点?root?，请你采用前序遍历的方式，将二叉树转化为一个由括号和整数组成的字符串，返回构造出的字符串。

空节点使用一对空括号对?"()"?表示，转化后需要省略所有不影响字符串与原始二叉树之间的一对一映射关系的空括号对。

（2）解题思路

? ? ? ? 根据题目要求，我们需要对字符串进行拼接，所以需要用到StringBuilder对象，基本思路就是利用递归进行前序遍历，在遍历过程根据题目要求进行增加“（）”，注意哪些“（）”是要进行省略是题目较为复杂的一点，剩下的相关条件判断在代码注释中进行讲解。

（3）代码实现

????????问题的实现代码如下，更多详细解释在代码注释中。

class Solution {
    //返回以前序遍历构建的字符串
    public String tree2str(TreeNode root) {
        StringBuilder tmp = new StringBuilder();
        tree2strChild(root,tmp);
        //StringBuilder转String用toString()方法
        return tmp.toString();
    }
    //将每棵子树构建的字符串都拼接到tmp中,拼接方法append()
    private void tree2strChild(TreeNode root, StringBuilder tmp) {
        //当前树是空树,直接返回不进行拼接
        if (root == null){
            return;
        }
        //将root的val拼接到tmp中
        tmp.append(root.val);
        if (root.left != null){
            //左子树不为空,进行递归拼接
            tmp.append("(");
            tree2strChild(root.left,tmp);
            tmp.append(")");
        }else {
            if (root.right != null){
                //左子树为空,右子树不为空,根据要求,()不能省略
                tmp.append("()");
            }else {
                //左右子树都为空,不继续进行拼接,直接返回
                return;
            }
        }
        if (root.right != null){
            //右子树不为空,进行递归拼接
            tmp.append("(");
            tree2strChild(root.right,tmp);
            tmp.append(")");
        }else {
            //右子树为空,根据要求不进行拼接,直接返回
            return;
        }
    }
}

• 尾声

? ? ? ? 本篇文章通过十道二叉树的经典题型对二叉树又进行了一个深刻的讲解，在解决二叉树相关问题时我们最常使用的方法就是递归，希望在读完这篇文章后友友们能对二叉树有更深的认识并且更加理解递归这一重要思想，今天的分享到此也将就要结束了，希望本篇文章会对友友们有帮助，当然文章如果有任何问题欢迎私信我或者留言至评论区，我都会仔细观看的，喜欢本篇文章的友友别忘了点赞和收藏，求求了~~你们的支持就是我最大的动力，我们下篇文章见。