JAVA算法-查找

目录

基本查找*：

二分查找*：

数据单调递增：

数据单调递减：

总结规律：

插值查找*：

斐波那契查找（了解原理）：以后补

分块 查找*：

特殊 情况（无规律的数据）：

以上小结：

哈希查找（了解原理）：以后补

树表查找（涉及数据结构）：以后补

---

基本查找*：

也叫线性查找，

从头到尾依次遍历

---

示例：

需求 1：定义一个方法利用基本查找，查询某个元素在数组中是否存在

 public static void main(String[] args) {
int[] arr = {1, 2, 3, 4, 5, 6};
System.out.println(search(arr, 4));
}
//方法
public static boolean search(int[] arr, int number) {
    for (int i = 0; i < arr.length; i++) {
        if (arr[i] == number) {
            return true;
        }
    }
    return false;
}

---

需求 2：定义一个方法利用基本查找，查询某个元素在数组中的索引

要求：不需要考虑数组中元素是否重复

public static void main(String[] args) {

    int[]arr={1,2,3,4,5,6,6,8,6};
    System.out.println(index(arr, 6));//5

}

public static int index(int[] arr, int number) {

    for (int i = 0; i < arr.length; i++) {
        if (arr[i] == number) {
            return i;
        }
    }
    return -1;
}

控制台：

5

---

需求 3：

要求：在上一题的基础上 需要考虑数组中元素有重复的可能性：

思路：也就是若有重复的数据，要返回多个索引，

我们可以用一个集合来存放索引（因为集合有 add 方法，添加方便）,最后遍历集合即可。

示例;

  public static void main(String[] args) {

        int []arr={1,2,2,2,3,2};
        ArrayList index = index(arr, 2);

        for (int i = 0; i < index.size(); i++) {
            System.out.println(index.get(i));
        }
    }
    public static ArrayList index(int []arr, int number){
        //核心：定义集合存放索引
        ArrayList<Integer>list=new ArrayList<>();
        for (int i = 0; i < arr.length; i++) {
            if (arr[i]==number){
                list.add(i);
            }
        }
        return list;
    }

---

二分查找*：

也叫折半查找：

前提条件：

• 元素必须是有序的，从小到大，或是从大到小，

核心逻辑：

• 每次排除一半的查找范围。

注意点:

• 如果是无序的，也可以先进行排序。但是排序后，会改变原有数据的顺序，也就是说元素对应的索引变了，这时再获取索引无意义，这是只能适用于查找数据是否存在再容器中。

---

数据单调递增：

如：

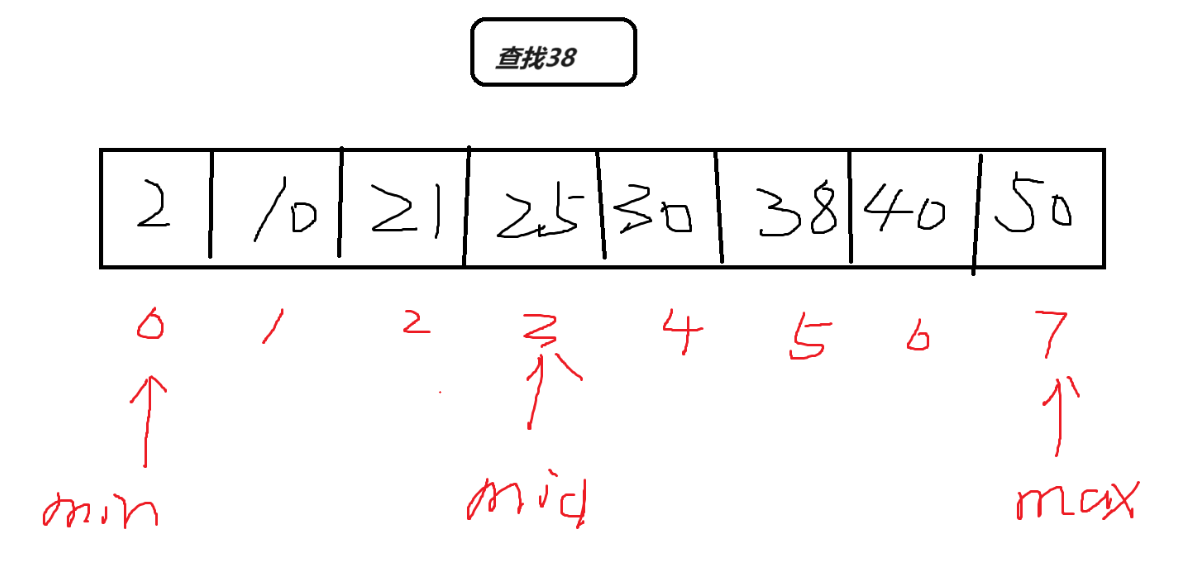
可以知道最小索引时 0

最大索引是 7

中间索引是：（0+7）/2=3

第一次查找中间索引对应的值是 25，

又因为是递增数组

所以说 38 一定在中间索引对应的值的右边。

这时我们可以让 min=mid+1（max 不用变，目的是缩小查找范围）

则下一次查找的区域索引 就 是 4~7。

代码语言可以这样写：

if(arr[mid]<number){

min=mid+1;

}

---

同理, 若我们要查找 21，

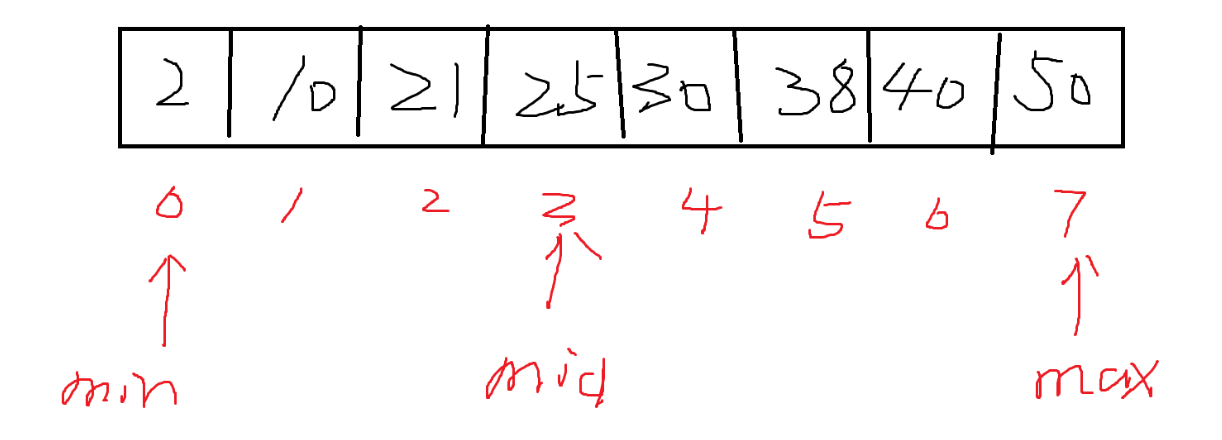
第一次查找 中间索引对应的值是 25，

又因为是递增数组

所以说 21 一定在中间索引对应的值的左边。

这时我们可以让 max=mid-1（min 不用变，目的是缩小查找范围）

则下一次查找的区域索引是 ： 0-2

代码语言：

if(number<arr[mid]){

max=mid-1;

}

---

之后的每一次查找 mid 索引值都会因为 min 或 max 的变化而变化，使得范围不断缩小。

---

数据单调递减：

以上是数据单调递增的情况：

单调递减的情况则相反：

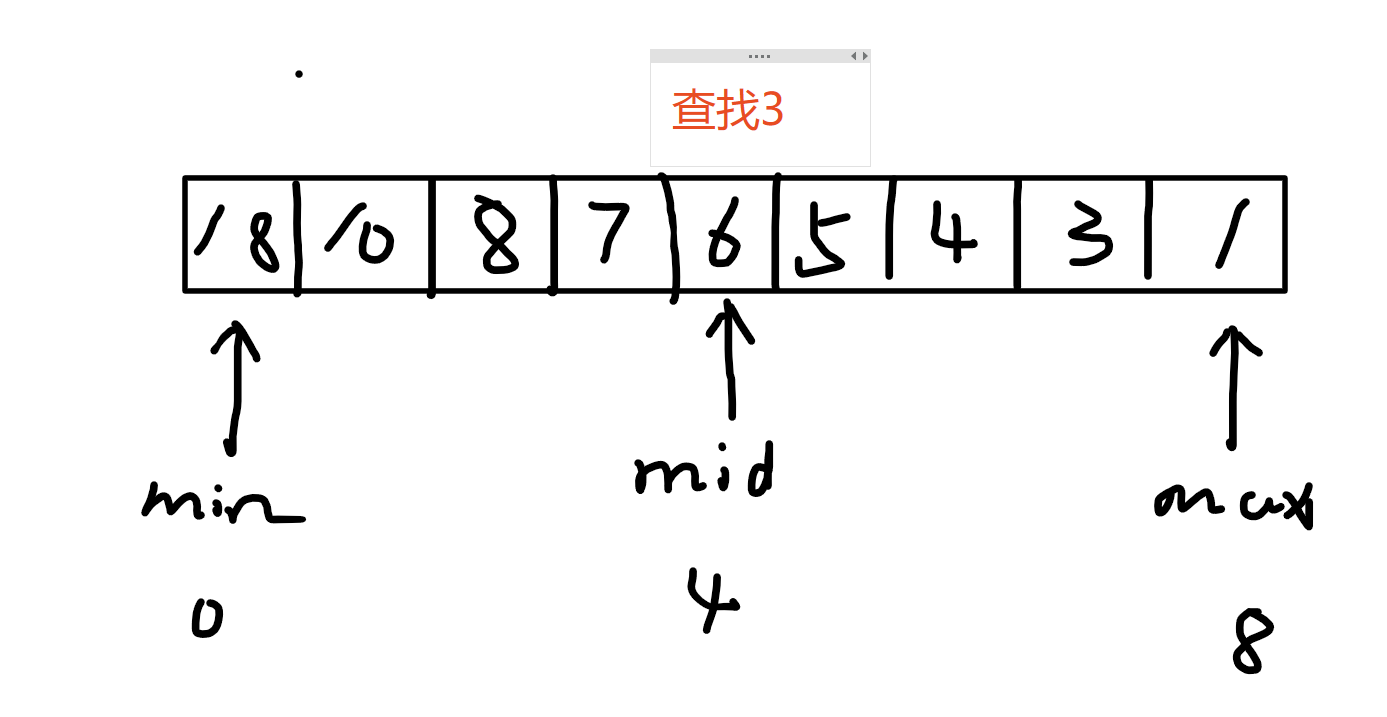
第一次查找 中间索引对应的值是 6，

又因为是递减数组

所以说 3 一定在中间索引对应的值的右边。

这时我们可以让 min=mid+1（max 不用变，目的是缩小查找范围）

则下一次查找的区域索引是 ： 5-8

代码语言：

if(number<arr[mid]){

min=mid+1

}

---

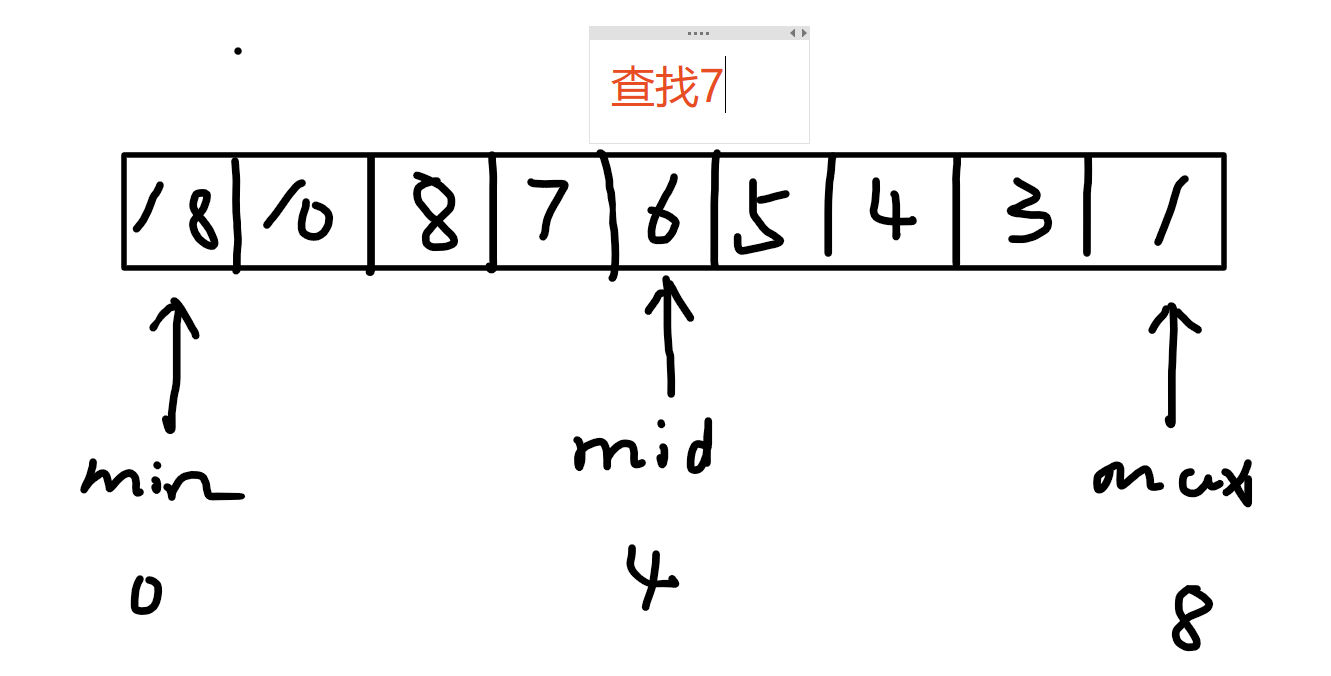
第一次查找 中间索引对应的值是 6，

又因为是递减数组

所以说 7 一定在中间索引对应的值的 左 边。

这时我们可以让 max=mid-1（min 不用变，目的是缩小查找范围）

则下一次查找的区域索引是 ： 0-3

代码语言：

if(number>arr[mid]){

max=mid-1;

}

之后的每一次查找 mid 索引值都会因为 min 或 max 的变化而变化，使得范围不断缩小。

---

总结规律：

• 要根据数组的单调性判断 number 和 arr [mid] 的位置关系。

当要查找的数据在中间索引对应的数据右边时（位置关系，无关大小），min =mid+1，max 不变。

当要查找的数据在中间索引对应的数据左边时（位置关系，无关大小），min 不变，max =mid-1。

---

例题：

代码除了要写上面讨论的中间索引对应值和目标值的关系

还要考虑中间索引恰好是要查的数的情况、查找数在数组中不存在的情况，具体如下

public static void main(String[] args) {
    //前提有序
    //需求：定义一个方法利用二分查找，查询某个元素在数组中的索引
    int[] arr = {7, 23, 79, 81, 103, 127, 131, 147};

    System.out.println(index(arr, 150));
}


public static int index(int[] arr, int number) {
    //定义两个范围记录查找范围
    int min = 0;
    int max = arr.length - 1;
    //不知道要循环多少次
    while(true){
        //先找中间位置--（注意放在循环内，会不断变化）
        int mid = (min + max) / 2;
        //如果中间索引恰好是要查的数，直接返回索引
        if (arr[mid] == number) {
            return mid;
        }else if (arr[mid] < number) {
            //要查的数在中间位置的右边，max不变
            min = mid + 1;
        }else if ( number<arr[mid] ) {
            //要查的数在中间位置的左边，min不变
            max = mid - 1;
        }
        //当出现这种情况了就表示查找的数在数组中不存在
        if (min>max){
            return -1;
        }
    }

}

---

插值查找*：

基于二分法，使 mid 更加靠近要查找的数字。

差值查找前提也是数据有序。

low,high 分别代表最低最高索引

---

如：

---

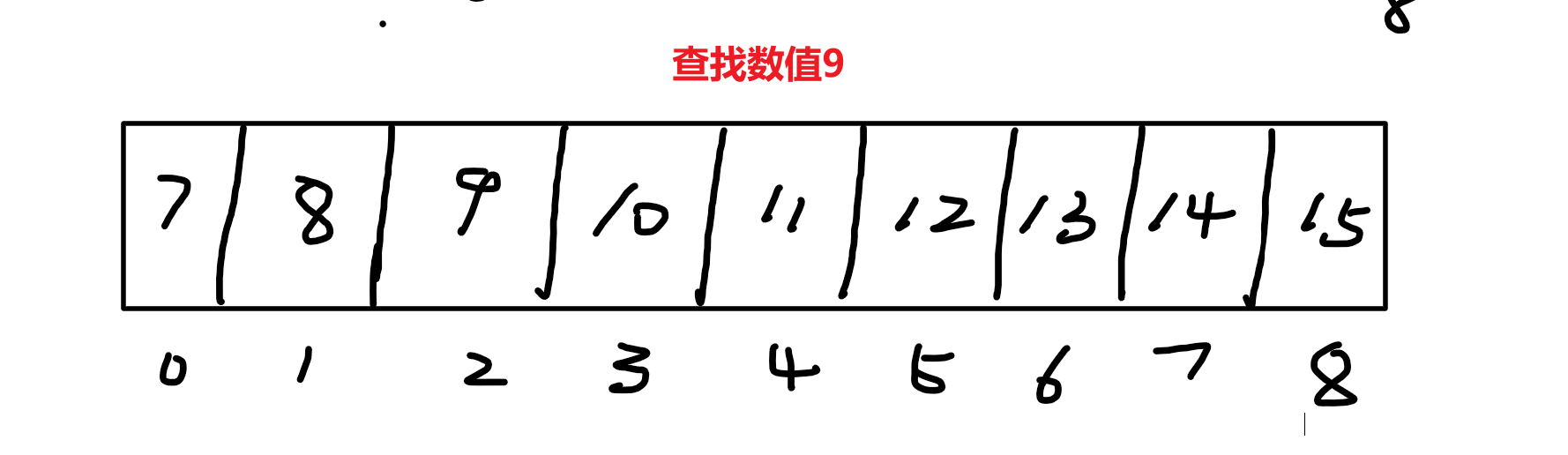
细节：对于表长较大，而关键字分布又比较均匀的查找表来说，插值查找算法的平均性能比折半查找要好的多。反之，数组中如果分布非常不均匀，那么插值查找未必是很合适的选择。

public static void main(String[] args) {
    //前提有序
    //需求：定义一个方法利用插值查找，查询某个元素在数组中的索引
    int[] arr = {7, 23, 79, 81, 103, 127, 131, 147};

    System.out.println(index(arr, 23));
}


public static int index(int[] arr, int number) {
    //定义两个范围记录查找范围
    int min = 0;
    int max = arr.length - 1;
    //不知道要循环多少次
    while(true){
         //先找中间位置--（注意放在循环内，会不断变化）
        int mid =min+(number-arr[min])/(arr[max]-arr[min])*(max-min);
        //如果中间索引恰好是要查的数，直接返回索引
        if (arr[mid] == number) {
            return mid;
        }else if (arr[mid] < number) {
            //要查的数在中间位置的右边，max不变
            min = mid + 1;
        }else if ( number<arr[mid] ) {
            //要查的数在中间位置的左边，min不变
            max = mid - 1;
        }
        //当出现这种情况了就表示查找的数在数组中不存在
        if (min>max){
            return -1;
        }

    }

}

代码和二分几乎一样，只要修改一下mid的计算方式即可

---

斐波那契查找（了解原理）：以后补

：根据黄金分割点来计算mid指向的位置

---

分块 查找*：

使用前提:

数据 块内无序，块间有序。

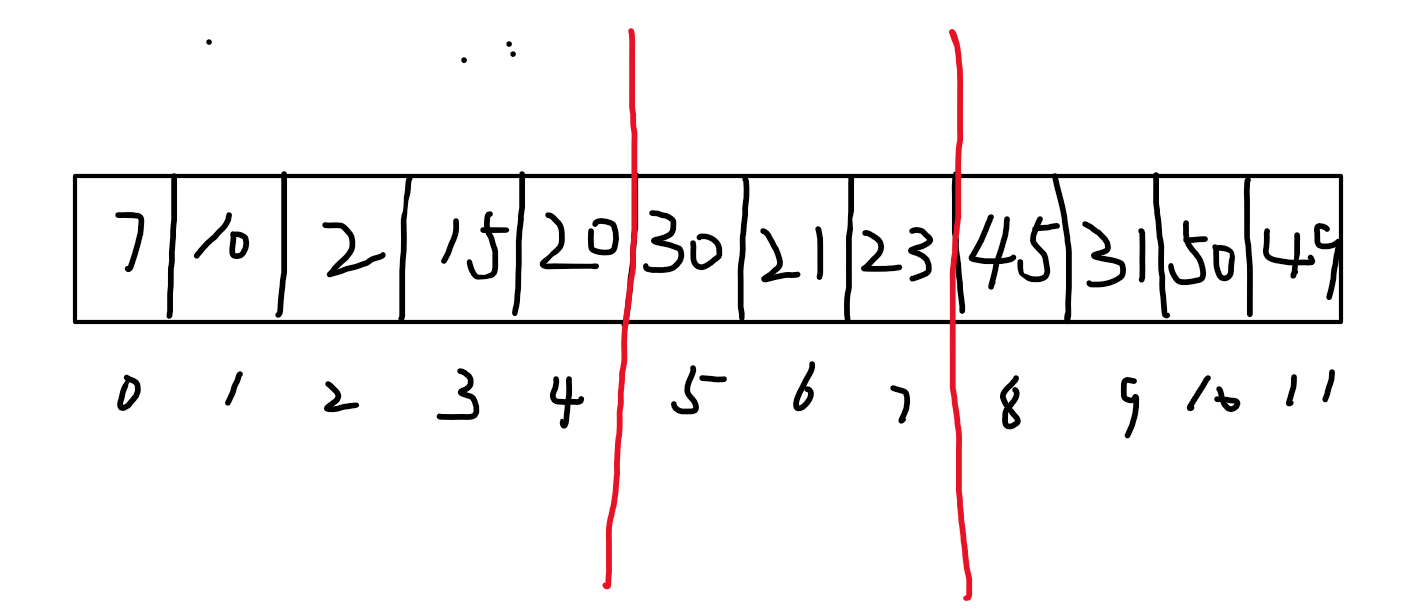
我们一般 分的块数为 数据个数开根号。

分的块必须保证，后一块的所有数都必须比前一块的最大值大。

---

• 分块查找的核心思想：

先确定目标数在哪一块当中，然后获取当前块的索引（会提前将每一块放入索引表中），然后在该块中遍历查找即可。

• 语言描述思路:

1. 我们分完块后，可以创建一个 Bolck 类描述不同的块，

内含属性：块内最大值、开始索引、结束索引

2.然后在测试类中创建不同块对象即可，并根据 数组数据 初始化对象属性即可

3.之后把对象存入 Block 类型的数组：

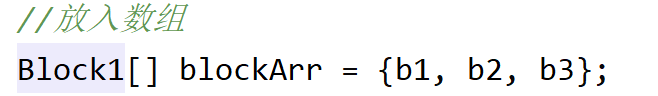
4.假设查找数字：

5.先定义一个方法看看这个数在哪一块中：

//注意if的判断条件和我们之前分块 规则 的关系

6.获取到数据所在块的索引后我们，就要开始用到另外两个属性 了

为方便演示另外再定义一个方法：

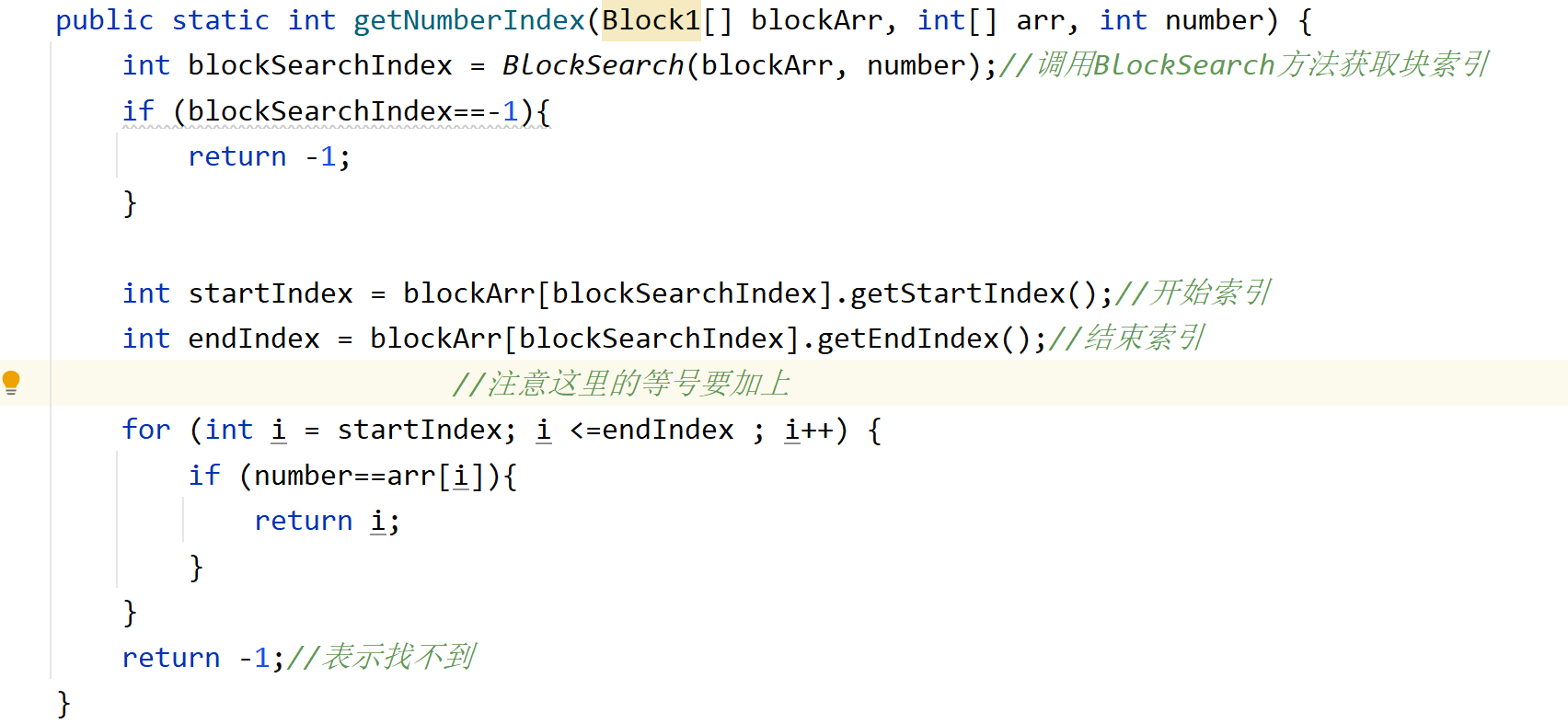
结束。

---

特殊 情况（无规律的数据）：

当不满足块内无序，块间有序，完全找不到规律时

分块思想：各块间不能有交集。

示例:

package com.lt.search;

public class BlockSearch2 {
    public static void main(String[] args) {
        //当不满足块内无序，块间有序，完全找不到规律时
        //分块思想：不能有交集
        int[] arr = {27,22,30,40,36,
                     13,19,16,20,
                     7,10,
                     43,50,48};

        Block b1=new Block(22,40,0,4);
        Block b2=new Block(13,20,5,8);
        Block b3=new Block(7,10,9,10);
        Block b4=new Block(43,50,11,13);
        Block []blocksArr={b1,b2,b3,b4};

        int number=48;
        
        int Index= getIndex(arr,blocksArr,number);
        System.out.println(Index);
    }
    //获取索引
    public static int getIndex(int[]arr,Block[] blocksArr,int number) {
        int blockIndex = getBlock(blocksArr, number);
        if (blockIndex==-1){
            return -1;//表示数字不在数组中
        }

        int startIndex = blocksArr[blockIndex].getStartIndex();
        int endIndex = blocksArr[blockIndex].getEndIndex();
        //注意等号
        for (int i = startIndex; i <=endIndex ; i++) {
            if(number==arr[i]){
                return i;
            }
        }
        return -1;//表示要查找的数在块中找没有

    }

    //先获取number'在哪个块中
    public static int getBlock(Block[]blocksArr,int number){
        for (int i = 0; i <blocksArr.length ; i++) {
           //分块思想决定了这里if的判断条件
            if (number<=blocksArr[i].getMax()&&number>=blocksArr[i].getMin()){
                return i;//返回块的索引
            }
        }
        return -1;//表示要查找的数不在任何块中

    }

}

class Block{
    private int min;
    private int max;
    private int startIndex;
    private int endIndex;
    //构造+set+get
}

---

以上小结：

• 基本查找： 数据没有任何顺序

• 二分查找、插值查找、斐波那契查找：

• • 数据一定要有顺序

• 二分查找，插值查找，斐波那契额查询各自的特点：
  相同点：
  都是通过不断的缩小范围来查找对应的数据
  
  不同点：
  计算mid的方式不一样
  二分查找：mid每次都是指向范围的中间位置
  插值查找：mid尽可能的靠近要查找的数据，但是要求数据尽可能的分布均匀
  斐波那契额查找：根据黄金分割点来计算mid指向的位置

---

哈希查找（了解原理）：以后补

---

树表查找（涉及数据结构）：以后补