深度学习入门（python）考试速成之Softmax-with-Loss层

发布时间：2023年12月28日

softmax函数：

交叉熵误差（Cross Entropy Error层）：

这里的\log表示以e为底数的自然对数(\log_{e})，即\ln，即L=- \sum_{k}t_{k}\log y_{k}=- \sum_{k}t_{k}\ln y_{k}。

y_{k}是神经网络的输出，t_{k}是正确解标签，t_{k}中只有正确解标签（表示）索引为1，其他均为0（one-hot表示）

假设正确解标签索引为“2”，与之对应的神经网络输出是0.6，则交叉熵误差为-\log0.6=0.51;若“2”对应的输出是0.1，则交叉熵误差为-\log0.1=2.30

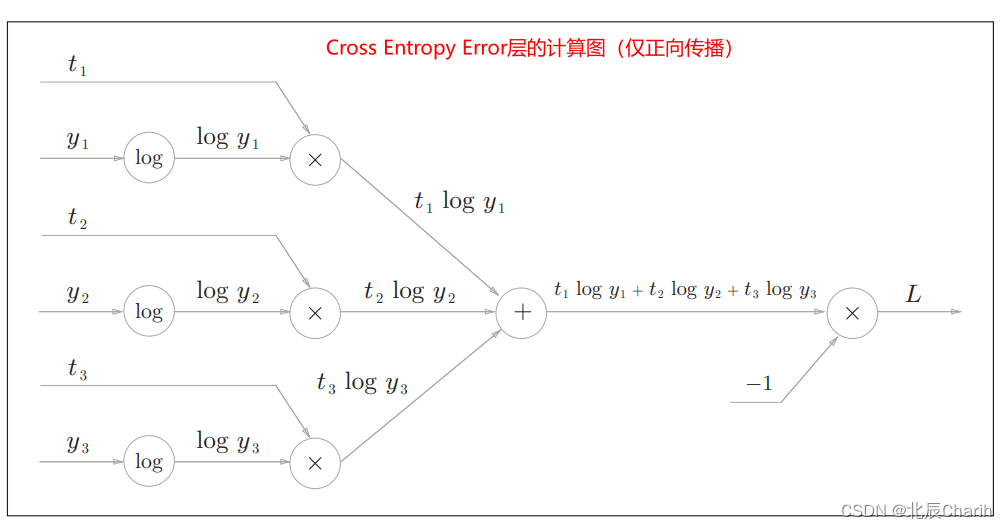
结果\begin{pmatrix} -\frac{t_{1}}{y_{1}} & -\frac{t_{2}}{y_{2}} &-\frac{t_{3}}{y_{3}} \end{pmatrix}是传给Softmax层的反向传播的输入。

Softmax层的反向传播

前面的层（Cross Entropy Error层）的反向传播的值传过来。

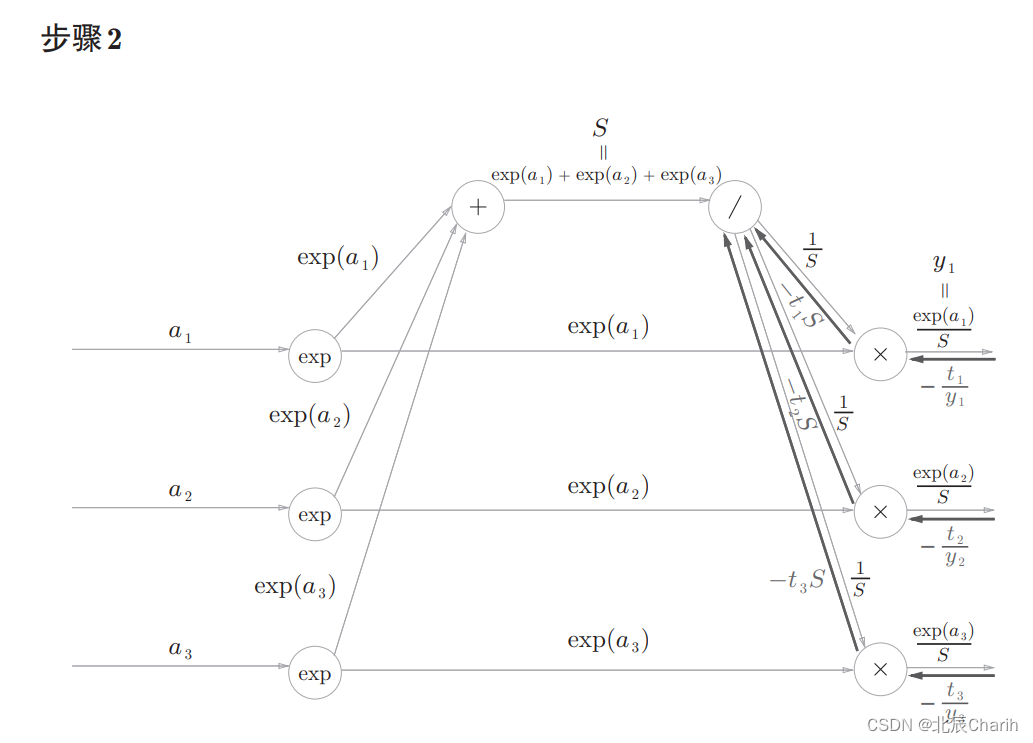
正向传播时若有分支流出，则反向传播时它们的反向传播的值会相加。 因此，这里分成了三支的反向传播的值(-t_{1}S,-t_{2}S, -t_{3}S)会被求和。然后， 还要对这个相加后的值进行“/”节点的反向传播，结果为 。 这里，\begin{pmatrix} t_{1} & t_{2} & t_{3} \end{pmatrix}是教师标签，也是one-hot向量。one-hot向量意味着\begin{pmatrix} t_{1} & t_{2} & t_{3} \end{pmatrix}中只有一个元素是1，其余都是0。因此，\begin{pmatrix} t_{1} & t_{2} & t_{3} \end{pmatrix}的和为1。

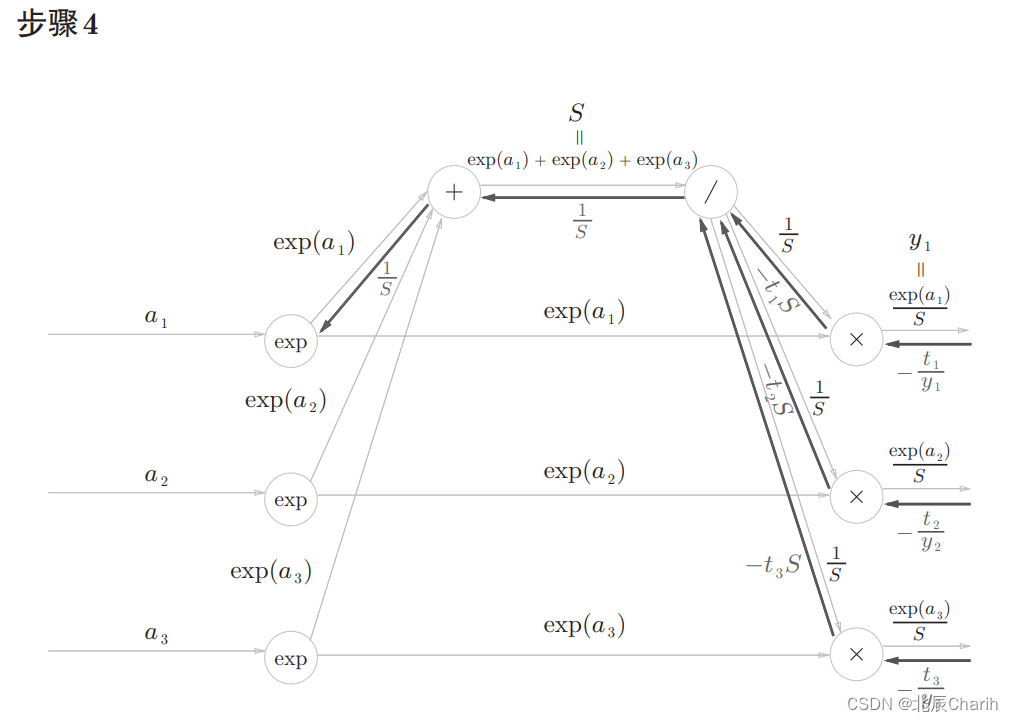
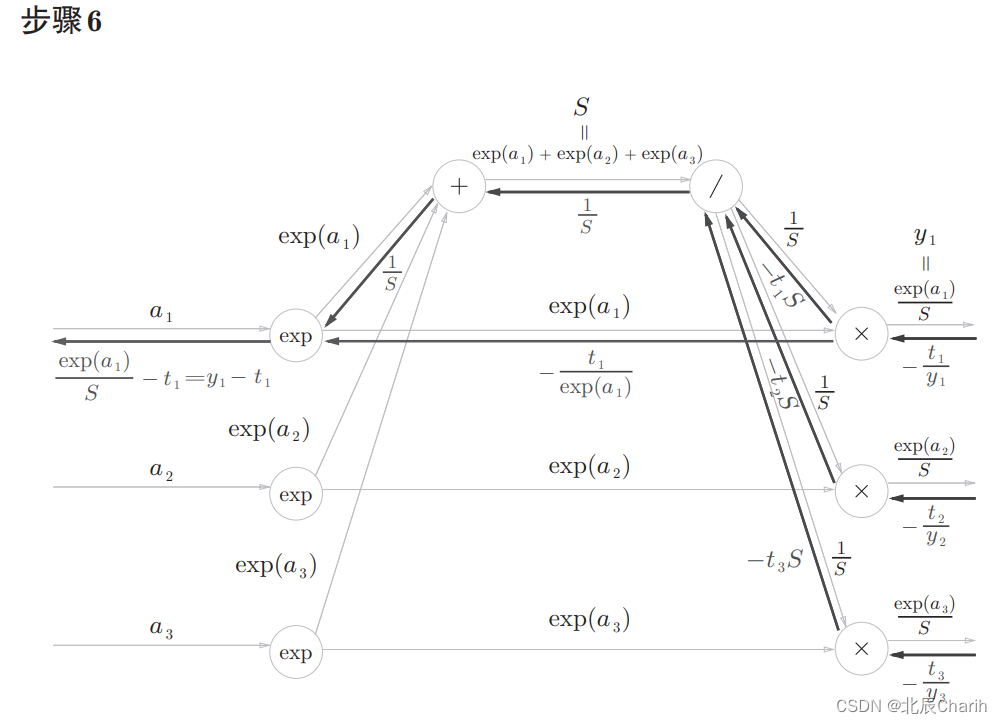
“+”节点原封不动地传递上游的值。

“×”节点将值翻转后相乘。这里，式子变形时使用了y_{1}=\frac{exp(a_{1})}{S}。

文章来源:https://blog.csdn.net/m0_62110645/article/details/135268945
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章