堆详解与优先级队列
导言:
我们知道队列是一种先进先出(FIFO)的数据结构,但是现实情况中,操作的数据有可能会有优先级,优先级高的数据要先出队。例如,医院的军人优先等等。而为此应运而生的就是优先级队列,java中可以使用PriorityQueue来创建,而其底层的实现则采用了堆这种数据结构。本文主要对堆和优先队列进行一个概述。
目录
正文
一.堆
1.概念:
堆(Heap)是一种特殊的树形数据结构,如果有一个关键码的集合K = {k0,k1, k2,…,kn-1},把它的所有元素按完全二叉树的顺序存储方式存储 在一个一维数组中,并满足:Ki <= K2i+1 且 Ki<= K2i+2 (Ki >= K2i+1 且 Ki >= K2i+2) i = 0,1,2…,则称为 小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。通俗来讲,就是把一组逻辑结构是完全二叉树的数据,存放在一个一维数组中,二叉树的根节点要么是最小的(小根堆)要么是最大的(大根堆)。
2.特点
- 堆是一个完全二叉树(Complete Binary Tree),即除了最后一层,其他层的节点都是满的,最后一层的节点都靠左排列。
- 堆中的每个节点都满足堆属性(Heap Property),即对于最大堆(Max Heap)来说,父节点的值大于或等于其子节点的值;对于最小堆(Min Heap)来说,父节点的值小于或等于其子节点的值。因此堆可以分为最大堆和最小堆两种类型:①大根堆:每个节点的值都大于或等于其子节点的值,即根节点是堆中的最大值。②小根堆:每个节点的值都小于或等于其子节点的值,即根节点是堆中的最小值。
3.存储方式
将元素存储到数组中后,可以根据二叉树章节的性质5对树进行还原。假设i为节点在数组中的下标,则有:
如果i为0,则i表示的节点为根节点,否则i节点的双亲节点为 (i - 1)/2
如果2 * i + 1 小于节点个数,则节点i的左孩子下标为2 * i + 1,否则没有左孩子
如果2 * i + 2 小于节点个数,则节点i的右孩子下标为2 * i + 2,否则没有右孩子

?4.堆的创建
建堆的思路通常是从最后一个非叶子节点开始,逐个向上调整节点的位置,使得满足堆的性质(最大堆或最小堆)。具体步骤如下:
- 从最后一个非叶子节点开始,最后一个非叶子节点的索引为n/2-1(其中n为堆的大小)。
- 从最后一个非叶子节点开始,依次向前遍历每个节点,对每个节点进行heapify操作。
- 在heapify操作中,比较当前节点与其左右子节点的值,找到最大(或最小)的节点,并与当前节点交换位置。
- 继续向前遍历,直到根节点,此时整个堆就满足了堆的性质。
大根堆代码如下:
?
import java.util.Arrays;
public class PriorityQueue1_21 {
public int[] elem;
public int usedSize;
public PriorityQueue1_21() {
this.elem = new int[10];
}
public void initElem(int[] array) {
for (int i = 0; i < array.length; i++) {
elem[i] = array[i];
usedSize++;
}
}
public void createHeap() {
for(int i = (usedSize-1-1)/2;i>=0;i--){
shiftDown(i, usedSize);
}
}
/**
* @param root 是每棵子树的根节点的下标
* @param len 是每棵子树调整结束的结束条件
* 向下调整的时间复杂度:O(logn)
*/
private void shiftDown(int root, int len) {
int child = root * 2 + 1;
while (child < len) {
if (child + 1 < usedSize && elem[child] < elem[child + 1]) {
child++;
}
if (elem[child] > elem[root]) {
swap(child, root);
root = child;
child = root * 2 + 1;
}
else{
break;
}
}
}
private void swap(int a, int b) {
int tmp = elem[a];
elem[a] = elem[b];
elem[b] = tmp;
}
public void printHeap() {
for (int i = 0; i < usedSize; i++) {
System.out.print(elem[i] + " ");
}
}
public static void main(String[] args) {
int[] arr = {5, 3, 8, 2, 7, 6};
PriorityQueue1_21 p = new PriorityQueue1_21();
p.initElem(arr);
p.createHeap();
p.printHeap();
}
}
输出结果为:
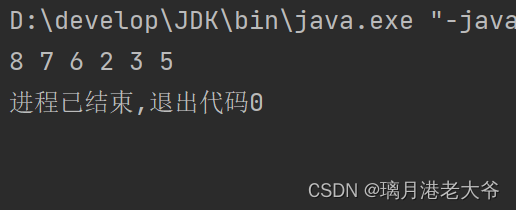
在上面的代码中,我们通过方法?createHeap来实现堆的建立过程。在?createHeap方法中,我们从最后一个非叶子节点开始,依次向前遍历每个节点,对每个节点进行shiftDown操作。shiftDown这段代码实现了堆的向下调整操作,用于维护堆的性质。在循环中,首先找到当前节点的左孩子,然后判断左右孩子中较大的节点,如果较大的孩子大于当前节点,则交换它们的值,并继续向下调整。这样可以确保以当前节点为根的子树满足堆的性质。建堆的时间复杂度较为复杂,可约等于n,所以建堆的时间复杂度为O(N)。
5.堆的插入与删除
插入操作:堆的插入实际上是优先队列添加一个元素,添加的元素都在数组的最后一个元素,我们只需要在插入元素后对堆进行调整即可。堆的创建需要向下调整,但是插入需要向上调整。
插入具体操作如下:
- 首先,我们将新元素添加到堆的末尾。
- 然后,我们需要通过向上调整(siftUp)操作来恢复堆的性质。具体来说,我们将新元素与其父节点进行比较,如果新元素的值大于其父节点的值,就交换它们,并继续向上比较,直到满足堆的性质为止。
代码如下:
/**
* 入队:仍然要保持是大根堆
*
* @param val
*/
public void push(int val) {
if(isFull()){
//插入前要判断受否满了,满了需要扩容
this.elem = Arrays.copyOf(elem,2*elem.length);
}
elem[usedSize] = val;
usedSize++;
//调用向上调整
shiftUp(usedSize-1);
}
private void shiftUp(int child) {
int parent = (child-1)/2;
while(parent>=0) {
if (elem[parent] < elem[child]) {
swap(parent, child);
child = parent;
parent = (child - 1) / 2;
}
else{
break;
}
}
}
public boolean isFull() {
return usedSize==elem.length;
}在?shiftUp?方法中,我们首先计算出新插入元素的父节点位置,然后进行循环比较。如果新元素大于其父节点,就进行交换,并更新新元素的位置为父节点,然后继续比较,直到新元素不再大于其父节点,或者到达堆顶为止。这样,通过向上调整的操作,我们可以确保在插入新元素后,堆的性质仍然得到保持。插入操作的时间复杂度也为O(log n)。
删除操作:
堆的删除实际上是优先级最高的元素出队,即堆顶元素。删除完后再重新向上调整一下堆的结构即可。
具体操作如下:
- 首先,我们将堆顶元素(最大元素)与堆的最后一个元素进行交换。
- 然后,我们需要通过向下调整(siftDown)操作来恢复堆的性质。具体来说,我们将交换后的堆顶元素与其子节点进行比较,如果它小于其子节点中的某一个,就与其中较大的子节点交换,并继续向下比较,直到满足堆的性质为止。
代码如下:
**
* 出队【删除】:每次删除的都是优先级高的元素
* 仍然要保持是大根堆
*/
public int pollHeap() {
int ret = elem[0];
swap(0,usedSize-1);
usedSize--;
shiftDown(0,usedSize-1);
return ret;
}
private void shiftDown(int root, int len) {
int child = root * 2 + 1;
while (child < len) {
if (child + 1 < usedSize && elem[child] < elem[child + 1]) {
child++;
}
if (elem[child] > elem[root]) {
swap(child, root);
root = child;
child = root * 2 + 1;
}
else{
break;
}
}
}?通过这样的思路,我们可以保证在插入和删除操作后,堆的性质仍然得到保持。这种实现方式的时间复杂度为O(log n),其中n是堆中元素的数量。
最后附上堆实现优先队列的完整代码:
import java.util.Arrays;
public class PriorityQueue1_21 {
public int[] elem;
public int usedSize;
public PriorityQueue1_21() {
this.elem = new int[10];
}
public void initElem(int[] array) {
for (int i = 0; i < array.length; i++) {
elem[i] = array[i];
usedSize++;
}
}
public void createHeap() {
for(int i = (usedSize-1-1)/2;i>=0;i--){
shiftDown(i, usedSize);
}
}
/**
* @param root 是每棵子树的根节点的下标
* @param len 是每棵子树调整结束的结束条件
* 向下调整的时间复杂度:O(logn)
*/
private void shiftDown(int root, int len) {
int child = root * 2 + 1;
while (child < len) {
if (child + 1 < usedSize && elem[child] < elem[child + 1]) {
child++;
}
if (elem[child] > elem[root]) {
swap(child, root);
root = child;
child = root * 2 + 1;
}
else{
break;
}
}
}
private void swap(int a, int b) {
int tmp = elem[a];
elem[a] = elem[b];
elem[b] = tmp;
}
/**
* 入队:仍然要保持是大根堆
*
* @param val
*/
public void push(int val) {
if(isFull()){
//插入前要判断受否满了,满了需要扩容
this.elem = Arrays.copyOf(elem,2*elem.length);
}
elem[usedSize] = val;
usedSize++;
//调用向上调整
shiftUp(usedSize-1);
}
private void shiftUp(int child) {
int parent = (child-1)/2;
while(parent>=0) {
if (elem[parent] < elem[child]) {
swap(parent, child);
child = parent;
parent = (child - 1) / 2;
}
else{
break;
}
}
}
public boolean isFull() {
return usedSize==elem.length;
}
/**
* 出队【删除】:每次删除的都是优先级高的元素
* 仍然要保持是大根堆
*/
public int pollHeap() {
int ret = elem[0];
swap(0,usedSize-1);
usedSize--;
shiftDown(0,usedSize-1);
return ret;
}
public boolean isEmpty() {
return usedSize==0;
}
/**
* 获取堆顶元素
*
* @return
*/
public int peekHeap() {
return elem[usedSize-1];
}
public void printHeap() {
for (int i = 0; i < usedSize; i++) {
System.out.print(elem[i] + " ");
}
System.out.println();
}
public static void main(String[] args) {
int[] arr = {5, 3, 8, 2, 7, 6};
PriorityQueue1_21 p = new PriorityQueue1_21();
p.initElem(arr);
p.createHeap();
p.printHeap();
p.push(10);
p.printHeap();
System.out.println(p.pollHeap());
}
}
二.优先级队列PriorityQueue
1.概念
Java集合框架中提供了PriorityQueue和PriorityBlockingQueue两种类型的优先级队PriorityQueue是线程不安全的,PriorityBlockingQueue是线程安全的,本文主要介绍PriorityQueue。
Java中的PriorityQueue是一个基于优先级堆的无界优先级队列。它是一个队列,其中每个元素都有一个优先级,优先级最高的元素最先被移除。上面堆的实现的思路和java底层的思路大同小异,所以只需在使用时直接创建该集合的对象即可。
2.特点
PriorityQueue的特点包括:
- 无界队列:PriorityQueue是一个无界队列,它可以根据需要动态增长。优先队列的扩容明:
如果容量小于64时,是按照oldCapacity的2倍方式扩容的
如果容量大于等于64,是按照oldCapacity的1.5倍方式扩容的
如果容量超过MAX_ARRAY_SIZE,按照MAX_ARRAY_SIZE来进行扩容 - 优先级顺序:元素按照它们的自然顺序或者根据构造队列时提供的Comparator进行排序。
- 堆实现:PriorityQueue内部使用堆来维护元素的顺序,通常是小根堆(最小元素在顶部)或者大根堆(最大元素在顶部)。
3.常用接口介绍
1.无参构造方法:创建一个初始容量为11的空优先级队列。
PriorityQueue<Integer> pq = new PriorityQueue<>();2.使用Comparator的构造方法:创建一个根据指定比较器进行排序的优先级队列。
// 自定义比较器类
class MyComparator implements Comparator<Integer> {
@Override
public int compare(Integer o1, Integer o2) {
// 自定义排序规则,例如按照元素的大小升序排列
return o1 - o2;
}
Comparator<Integer> comparator = new MyComparator();
// 自定义比较器
PriorityQueue<Integer> pq = new PriorityQueue<>(comparator);3.使用初始容量和Comparator的构造方法:创建一个具有指定初始容量,并根据指定比较器进行排序的优先级队列。
// 自定义比较器类
class MyComparator implements Comparator<Integer> {
@Override
public int compare(Integer o1, Integer o2) {
// 自定义排序规则,例如按照元素的大小升序排列
return o1 - o2;
}
int initialCapacity = 20;
Comparator<Integer> comparator = new MyComparator(); // 自定义比较器
PriorityQueue<Integer> pq = new PriorityQueue<>(initialCapacity, comparator);
4.添加元素:使用offer(E e)方法向队列中添加元素。
PriorityQueue<Integer> pq = new PriorityQueue<>();
pq.offer(3);
pq.offer(1);
pq.offer(2);5.获取并移除队首元素:使用poll()方法获取并移除队列中优先级最高的元素。
int firstElement = pq.poll();
System.out.println("队首元素:" + firstElement);
6.获取但不移除队首元素:使用peek()方法获取但不移除队列中优先级最高的元素。
int peekElement = pq.peek();
System.out.println("队首元素(不移除):" + peekElement);7.获取队列中的元素数量:使用size()方法获取队列中的元素数量。
int size = pq.size();
System.out.println("队列中的元素数量:" + size);8.清空队列中的所有元素:使用clear()方法清空队列中的所有元素。
pq.clear();通过这些方法,我们可以对PriorityQueue进行常见的操作,包括插入元素、获取并移除队首元素、获取但不移除队首元素、获取队列中的元素数量以及清空队列中的所有元素。
总结:
总的来说,堆是一种数据结构,而优先级队列是基于堆实现的一种数据结构。堆和优先级队列通常用于解决一些需要按照优先级处理元素的算法和问题,比如Dijkstra算法、最小生成树算法、调度算法等。想要掌握好堆和优先级队列关键要掌握向上调整和向下调整两个方法,希望本文对你有所帮助。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- xxljob分布式调度平台
- NFC与ZigBee技术在智慧农业物联网监测系统中的应用
- Android 车联网——CarDiagnosticService介绍(十八)
- 2024年在国内升级ChatGPTplus方法--(仅需微信支付宝)
- 2036开关门,1109开关门
- 老薛主机购买域名优惠码是多少?
- 阿里云部署k8s with kubesphere
- nodejs+vue+微信小程序+python+PHP在线学习与推荐系统设计与实现-计算机毕业设计推荐
- 一篇文章学会使用 NestJS 的 Module 实现高效的代码模块管理
- 社群管理助手的角色与价值