【Simulink系列】——用扫地机器人实例快速引入

Simulink 的主要功能是对系统各个组件随时间流逝的行为变化进行仿真。简单来讲就是：采用一个时钟，按时间确定各个模块的仿真顺序，并在仿真过程中依次将在上一个模块图中计算得出的输出传播到下一个模块，直至最后一个模块。以扩音器为例。在每个时间步，Simulink 都必须计算正弦波的值，将其传播给扩音器，然后计算输出值。

在每个时间步，每个模块都要根据输入计算输出。当在一个给定时间步计算完图中的所有信号后，Simulink 将基于模型配置和数值求解器算法确定下一个时间步，并向前移动仿真时钟。接下来，每个模块将为这个新的时间步计算输出。

在仿真中，时间的移动与真实时钟不同。完成每个时间步的计算需要多长时间，该时间步就会花费多长时间，而不管它代表几分之一秒还是几年。

通常，组件的输入对其输出的影响不是瞬时的。例如，打开加热器不会导致温度立即发生变化。该动作为微分方程提供输入。历史温度（一个状态）也是一个输入因子。当仿真需要求解微分方程或差分方程时，Simulink 使用内存和数值求解器来计算时间步的状态值。

Simulink 处理三类数据：

信号 - 在仿真期间计算的模块输入和输出

状态 - 在仿真期间中计算的代表模块动态的内部值

参数 - 影响模块行为的值，由用户控制

在每个时间步，Simulink 都计算信号和状态的新值。相比之下，我们可以在编译模型时指定参数，并且可以在仿真运行时偶尔更改它们。

2、仿真基本流程

Simulink 在库浏览器中提供了一系列按功能分类的模块库。下面是常用的一些模块库：

Continuous - 表示具有连续状态的系统的模块

Discrete - 表示具有离散状态的系统的模块

Math Operations - 实现代数和逻辑方程的模块

Sinks - 存储并显示所连接信号的模块

Sources - 生成模型的驱动信号值的模块

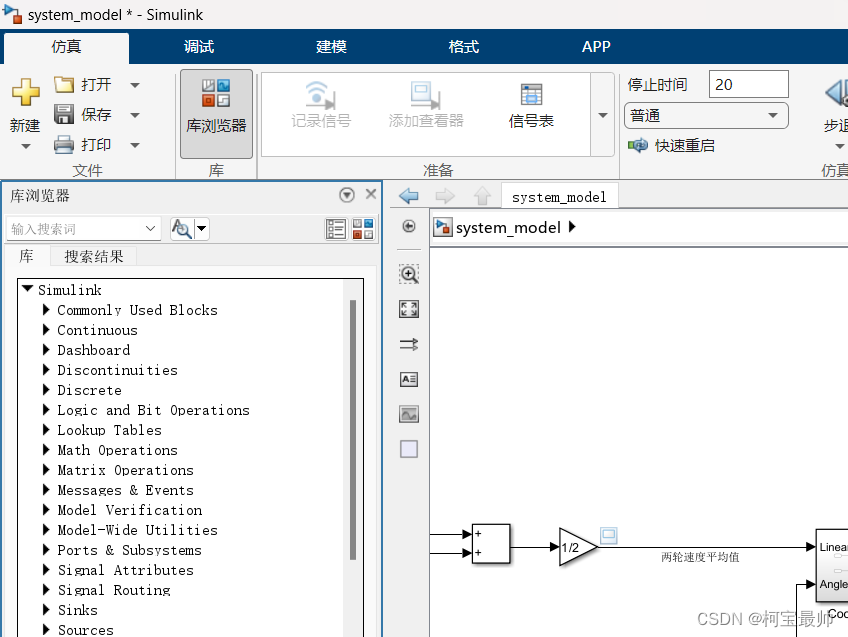
可以在库中寻找合适模块（也可以双击空白处进行模块搜索）进行连接，建立自己需要的系统，由于simulink的交互式很强，这里不多赘述！

连接完成后需要指定仿真的停止时间，默认停止时间?10.0?适合此模型。此时间值没有单位。Simulink 中的时间单位取决于方程的构造方式。例如对简化的汽车运动进行 10 秒的仿真，其他模型的时间单位可以是毫秒或年。

仿真雏形成功后可根据实际场景对模型进行细化、优化等！可对信号添加注释、利用显示模块scope等查看、比较信号等。

3、调试技巧

①信号属性

信号具有与其在模型中的函数对应的属性：

维度 - 标量、向量或矩阵

数据类型 - 字符串、双精度、无符号整数等

采样时间 - 信号产生更新值的固定时间间隔（对于连续采样，则为?0）

要显示一个模型中所有信号的数据类型，请在调试选项卡的叠加信息下，点击基本数据类型。大多数信号均为双精度double，只有名为?Alert system?的子系统的输出例外。

要显示采样时间，请在调试选项卡的叠加信息下，点击“采样时间”部分的颜色。模型会更新以将模型中的各个采样时间显示为不同颜色，并显示图例。

黑	连续动态的模块或信号：具有连续采样时间的信号会根据求解器的要求频繁更新以满足指定的容差值。
品红	保持不变的模块或信号：它们在仿真过程中保持不变。
红	最低固定时间间隔更新的离散模块或信号：具有离散采样时间的信号会以固定间隔更新。如果模型中包含具有不同固定采样时间的组件，则每个离散采样时间显示为不同的颜色。
黄	同时包含离散和连续信号的多速率子系统。

②跟踪信号

模型有常量输入和离散输出。要确定采样方案从哪里发生改变，可以通过其信源模块跟踪各个模块的输出信号。

要打开模型浏览器，请垂直展开模型窗口，直到“隐藏/显示模型浏览器”按钮">>"，?出现在 Simulink 编辑器的左下角。然后，点击“隐藏/显示模型浏览器”按钮。
要开始跟踪输出信号的源，请选择该信号。然后，在信号选项卡中，点击跟踪到源?

Simulink 编辑器进入信号跟踪模式。在信号跟踪模式下，模型画布变为灰色而不是白色，以帮助突出跟踪的路径。提示面板显示在信号跟踪模式下可以采取的操作的提示，以及对应于每项操作的键盘快捷方式。要最小化该提示面板，请按键盘上的“???”键。如果您要还原该提示面板，请按再次键盘上的“??”。
按向左箭头键可继续跟踪输出信号的源。到达信号路径中的?Subtract?模块时，必须选择一条路径来继续跟踪，因为?Subtract?模块有两个输入端口。
注意每个端口名称的颜色反映端口的采样时间。

二、基于模型的simulink设计实例（两轮扫地机器人）

利用基于模型的设计，可以快速且经济高效地开发动态系统，包括控制系统、信号处理系统和通信系统。

1、系统定义与布局

对象：家用扫地机器人，借助两个轮子进行移动或旋转，假设机器人以下列两种方式之一进行移动（假设这两种运动都从静止状态开始，假设两轮速度大小相同，方向可不同）

线性	两个轮子以相同的速度向同一方向转动，机器人线性移动
旋转	两个轮子以相同的速度向相反方向转动，机器人原地旋转

如下图为机器人的底面视角：

确定建模目的

目的和需求决定了模型结构和详细程度。

如果目的只是弄清楚机器人可以走多快，那么只对线性运动进行建模就足够了。
如果目的是为设备设计一组输入，使它按照给定的路径移动，那就会涉及到旋转组件。
如果目的是避障，那么系统就需要一个传感器。

我们的目的是设计一些传感器参数，使机器人能够在检测到路径中的障碍物时及时停止：

确定电机停止后机器人多长时间能停止下来（分析运动，以便设计传感器）

提供一系列线性运动和旋转运动的命令，能够在二维空间内移动（以便测试）

确定系统组件和接口

确定顶层结构的各个组件及其关系有助于以系统化方式构建比较复杂的模型。

系统需要哪些结构组件和功能组件？

当布局能够反映物理结构和功能结构时，将有助于理解、构建、进行通信和测试系统。

此扫地机器人模型包括：两个相同的轮子、施加在轮子上的输入作用力、旋转动态特性、坐标变换和一个传感器。可使用?Subsystem?表示每个组件：

每个组件的输入和输出（接口）是什么？

绘制一个显示各组件连接情况的图形，可视化模型中的信号流，确定每个信号的信源和信宿，
并确定是否所有必要的组件都存在。

一些模块输入与前面模块输出并不完全匹配，如旋转模块的输入需要计算两轮速差/2、坐标变换输入需要计算两轮的平均速度、传感器的输入是对坐标变换的输出速度进行积分（1/s的初始条件可以设置保留为0）。

需要达到多高的详细程度，并设置合适的参数和数据？

在图中包括主要系统参数。绘制系统图可以帮助识别并建模对要观察的行为非常重要的部件。
每个组件和参数在模型中都要有一个对应的表示，但需要权衡模型的复杂程度和可读性。
可以从具有很少细节的简要模型开始，然后根据需要逐渐提高复杂程度。

参数	模块	符号	值	类型
质量	左轮右轮	`m`	2.5 kg	可变
滚阻	左轮右轮	`k_drag`	30 Ns2/m	可变
机器人半径	旋转	`r`	0.15 m	可变
初始角度	旋转	无	0 rad	固定
初始速度	左轮右轮	无	0 m/s 0 m/s	固定
初始 (X, Y) 坐标	积分器	无	(0, 0) m	固定

可使用 MATLAB工作区来计算参数。可在 MATLAB 命令行窗口中设置这些参数：

m = 2.5;
k_drag = 30;
r = 0.15;

确定系统布局

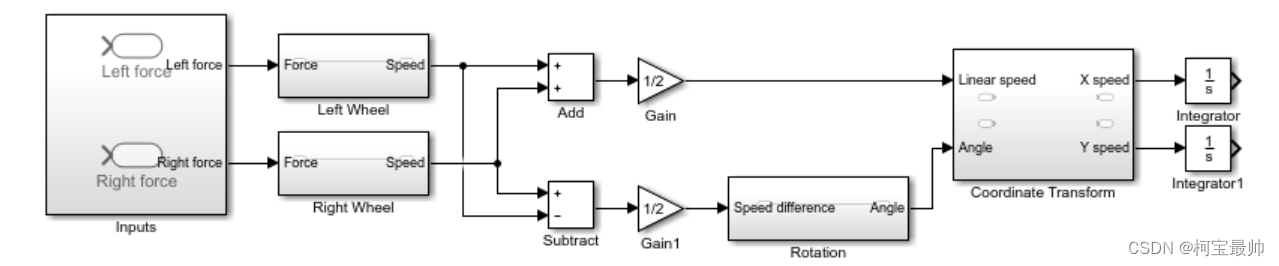
?以上布局模型可双击文件夹.slx文件打开，也可在 MATLAB命令行中，输入：

open_system('system_layout.slx')

2、建模并验证系统

对组件建模

下面，可以对每个组件（subsystem）具体进行建模，以表示该组件的物理行为或功能行为。物理组件/功能组件模型变量（输入输出）之间的关系有以下几种：

显式数学关系	可以根据组件的输入通过代数计算和微分方程积分，直接或间接计算出组件的输出
隐式数学关系	由于变量之间相互依赖，因此为组件指定输入和输出并不容易。例如，电路中连接的电机的?`+`?极电压和?`-`?极电压之间就存在一种隐式关系。要在 Simulink 中对这种关系进行建模，您可以使用 Simscape?等物理建模工具，也可以将这些变量建模为允许定义输入/输出的更大组件的一部分
测得实际组件的输入/输出数据	但不存在完全定义的数学关系。许多设备具有符合此描述的未建模组件。例如，电视机散发的热量。您可以使用 System Identification Toolbox来定义此类系统的输入/输出关系
显式功能定义	根据功能组件的输入通过代数计算和逻辑计算来定义功能组件的输出。例如，调温器的开关逻辑。可以将大多数功能关系建模为 Simulink 模块和子系统

对于本例的扫地机器人我们属于对显式输入/输出关系的物理组件和功能组件进行建模！

①物理组件建模

即描述组件之间的关系，例如数据、能量和力的传递。在 Simulink 中使用系统方程构建系统的图形化模型。建模之间需要明确：组件的常量？变量？多少个状态变量？

大多数系统方程大都属于以下三种类别之一：

连续系统：微分方程描述变量的变化率，为所有时间值都定义方程

例如，一阶微分方程给出车速：

$\frac{d v(t)}{d t}=-\frac{b}{m} v(t)+u(t)$

离散系统：差分方程描述变量的变化率，但只在特定时间定义方程

例如，来自离散比例微分控制器的控制信号：

$p d[n]=(e[n]-e[n-1]) K_d+e[n] K_p$

没有导数的方程是代数方程

例如，用代数方程表示包含两个组件的并联电路中的总电流：

$I_t=I_a+I_b$

物理组件1：轮子和线性运动

作用在轮子上的力包括电机施加的力（F）和阻力（Fdrag 是速度的函数），由牛顿第一定律：

$\begin{aligned} (m / 2) \dot{V} & =F-F d r a g \\ (m / 2) \dot{V} & =F-k \text { drag } V|V| \\ \dot{V} & =\frac{F-k \text { drag } V|V|}{(\mathrm{m} / 2)} \end{aligned}$

其中 kdrag?是阻力系数，m 是机器人的质量。每个轮子承载机器人一半的质量。创建的轮子如下，左右轮子相同：

这里创建阻力时用到了Matlab function模块，输入以下代码，并编辑数据将k_drag作用域设置为参数：

function Fdrag=get_fdrag(V,k_drag)

Fdrag=k_drag*V*abs(V);

两轮速度之和的1/2（平均值）作为线性速度值（直线速度）。这里假设轮子的速度大小始终相等，比如左轮2m/s、右轮2m/s，线性速度2m/s。

物理组件2：旋转运动

当两个轮子沿相反方向转动时，它们沿半径为?r?的圆周运动，从而产生机器人的旋转运动。则两个轮子速度 VR?与 VL?之差（分正负）的1/2作为输入，旋转运动作为输出，比如左轮2m/s、右轮-2m/s，旋转线速度2m/s（机器人自转）。则旋转角速度表示为：

$\dot{\theta}=\frac{(V_R-V_L)/2}{2 r}$

②功能组件建模

坐标变换

机器人在 x 和 y 坐标上的速度 VX?和 VY 可根据线性运动速度 VN?和角度 θ正交分解得到：

$\begin{aligned} & V_X=V_N \cos (\theta) \\ & V_Y=V_N \sin (\theta) \end{aligned}$

此处用到了SinCos?模块，乘法运算使用了 Product?模块。

③设置模型参数

参数	符号	值
质量	`m`	2.5 kg
滚阻	`k_drag`	30 Ns2/m
机器人半径	`r`	0.15 m

可以访问使用 MATLAB 工作区中的变量定义的参数值。通过在 MATLAB 命令行窗口中输入命令来定义以下变量。

m = 2.5;
k_drag = 30;
r = 0.15;

仿真验证组件

然后可通过使用测试数据对组件进行仿真，以验证组件的基本行为（提供输入并观察输出），验证单个组件时，可新建一个模型并复制该组件到该模型中进行。

针对本例验证的行为主要有：

当向轮子连续施加力时，速度会增加，直到达到稳定状态的速度为止

当两个轮子向相反方向转动时，旋转角度以恒定速率增加

首先需要创建一个测试输入，可使用Step?模块，并将其连接到名为?Right Wheel?的子系统的输入，将步长时间参数设置保留为?1。添加一个scope波形查看器可查看输出。

仿真结果表明：

①在步长时间处施加力之前，不会发生运动。施加力后，速度开始增加，当施加的力和阻力达到平衡后，速度将保持稳定。除验证外，此仿真还显示在给定的作用力下轮子的最大速度。

②当两个轮子以相同速度向相反方向转动时，角度会稳定增加。可以添加增益为180/pi的Gain?模块，将输出信号单位从弧度转换为角度；或者添加具有函数?mod?的?Math Function?模块，以 360 度为周期显示输出值，使角度输出更容易解释。

验证模型

验证单个组件后，您可以对整个模型进行类似的验证。此示例验证以下行为：

当沿相同方向对两个轮子施加相同的力时，机器人沿直线运动。
当沿相反方向对两个轮子施加相同的力时，机器人原地旋转。

由于此例较为简单，此处不再赘述！

3、添加新功能——传感器模块

通过上面的基本建模，我们得到了下面的简易系统雏形：

下面我们主要设计一个警报系统。需要确定用于测量障碍物距离的传感器的参数，警报系统按固定时间间隔对这些测量值进行采样，使输出与测量值相差始终不超过 0.05 米。系统会及时生成警报，让机器人在碰到障碍物前停下来。

通过仿真确定下面问题

如果切断轮子的电源，机器人能够以最高速度行驶多远
机器人的最高速度

删除现有step模块力输入，并添加一个 Pulse Generator 模块。设置参数：

幅值	1
周期	20
脉冲宽度（周期百分比）	15

采用以上参数值是为了确保达到最高速度，脉冲宽度15%即在第3秒（20x0.15）时脉冲停止（模拟断电），也可更改参数以查看其效果。运行模型 20 秒。下图scope左为直线速度，右为位移：

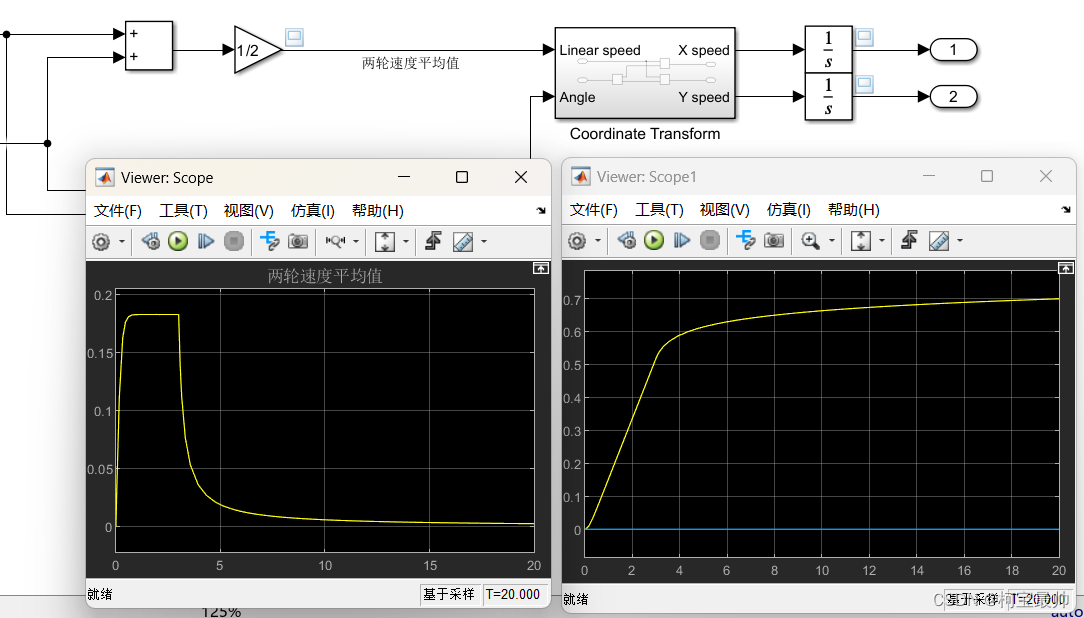仿真结果分析：

①在时间值为1左右达到最大值，时间值?3?时切断电源，此时速度迅速开始下降。然后速度逐渐接近零，但不会完全达到零。这是建模的局限性；无外力作用下的低速动态特性需要更复杂的表示。但针对本示例的目的，我们可以取近似值。

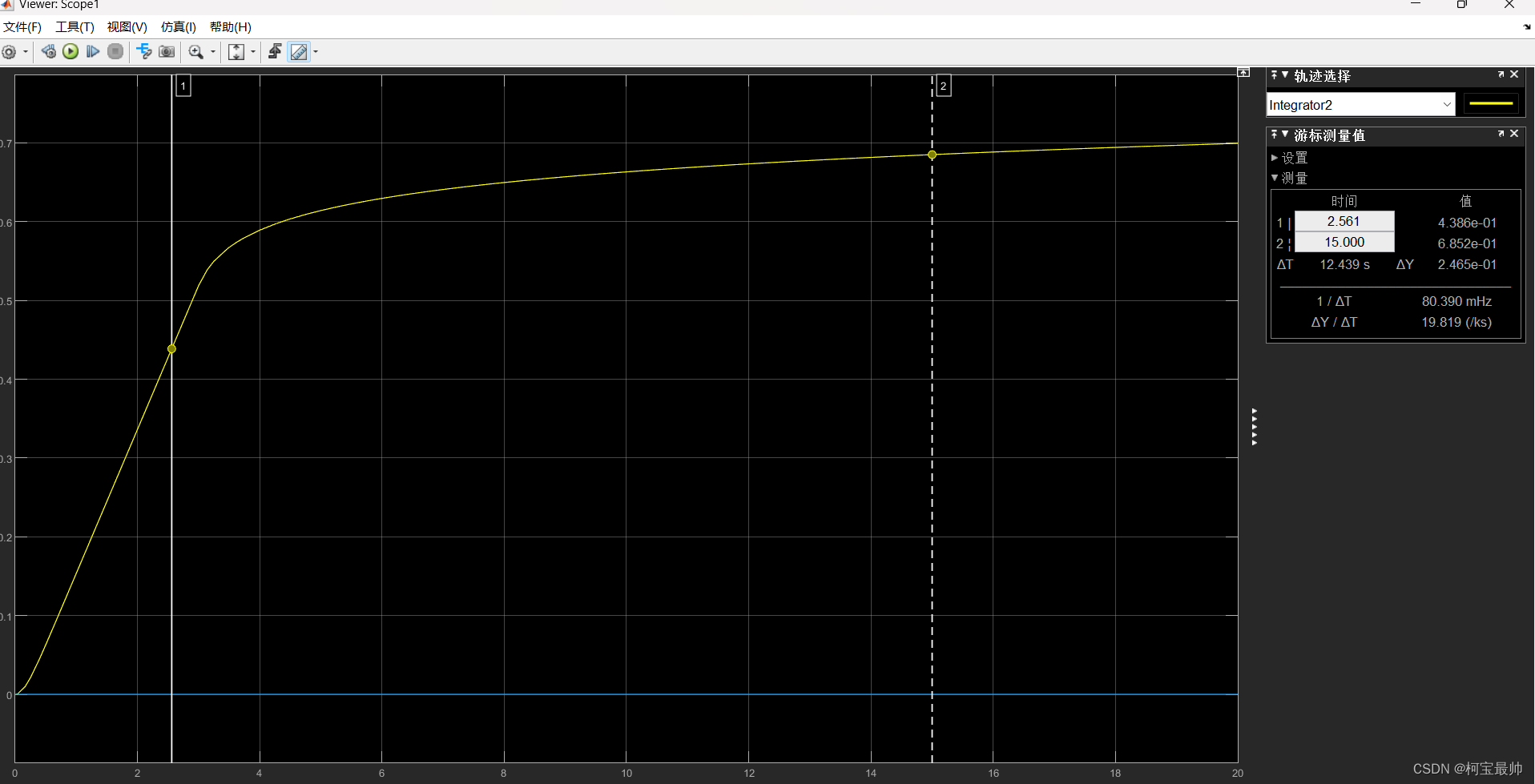
②在时间值为?3?时，机器人的位置大约在 0.55 米处。当仿真结束时，位置值小于 0.71 米。可以肯定地说，机器人在切断电源后行驶距离不到 0.16 米，由此解决了第一个问题。必须从距离障碍物 0.16 米处开始减速。但实际警报距离还必须将离散测量误差 0.05 米考虑在内。

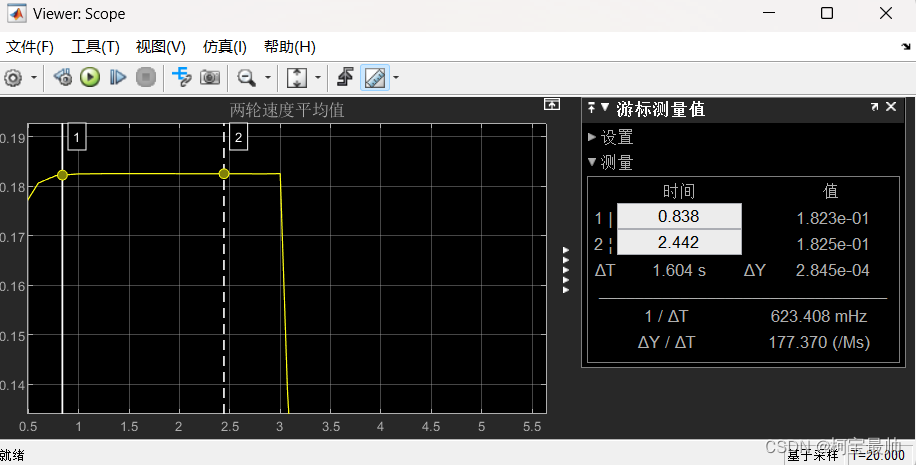
测量得到最高速度为0.1825m/s，由于传感器测量误差要求低于0.05m，最短用时0.05/0.1825=0.27s，所以采样间隔必须小于0.27s，取0.25s。

构建传感器组件

创建subsystem，并在内部进行各环节的建模：

采样环节利用Zero-Order Hold?模块，并将其采样时间参数设置为?0.25；警报逻辑采用Compare to Constant 模块，并设置参数如下，此逻辑模块在输入小于或等于 0.21 时输出 1。

`运算符`	`<=`
`常量值`	`0.21`
`输出数据类型`	`boolean`

仿真验证设计

以 X = 0.65, Y = 0 的障碍物位置来测试设计。此测试验证 X 方向的设计功能。您可以针对不同路径创建类似的测试。此模型仅生成警报，不控制机器人。

注意观察，alert在2.5s左右开始响应为1，即此时机器人位置与障碍物位置之间的距离（0.65-x位移）在 0.21 米范围内。再对比前面的x位移scope可发现此时x位移在0.44左右，符合实际情况。

拓展

也将深入分析此系统，再添加新的功能！对于本例可以考虑以下目标：

设计一个控制器，它可以改变作用力输入，使轮子按所需的速度转动

设计输入，使设备沿预定的路径移动

设计一个传感器和一个控制器，使设备沿直线移动

设计一种规划算法，使设备沿可能的最短路径到达某个点并避开障碍物

设计一个传感器和一种算法，使设备在某个区域内移动并避开障碍物

文章来源:https://blog.csdn.net/weixin_51658186/article/details/135186543
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！