数据结构与算法（九）--链表与递归
一、前言
之前的文链表的学习我们学习了链表的定义，以及链表的CRUD操作。并且通过链表去自定义了我们的栈和队列。但是链表还有很多很重要的性质，例如链表本身具有天然的递归性，我们可以利用链表的这些性质去完成一些需求。
二、链表和递归
很多人会将递归与树联系起来，事实上也确实如此，在树这样的结构中，使用递归是非常自然的，更重要的是使用递归是非常方便的，但是链表这种结构也是可以使用递归的，这是以为链表本身就具有天然的递归性。只不过由于联表结构太过于简单，它只是一个线性结构，所以我们直接用循环也可以很简单的解决链表上的问题，但是我们可以从链表开始就去接触下递归，为后续树的学习打下基础。
这里我们以leetCode203为例
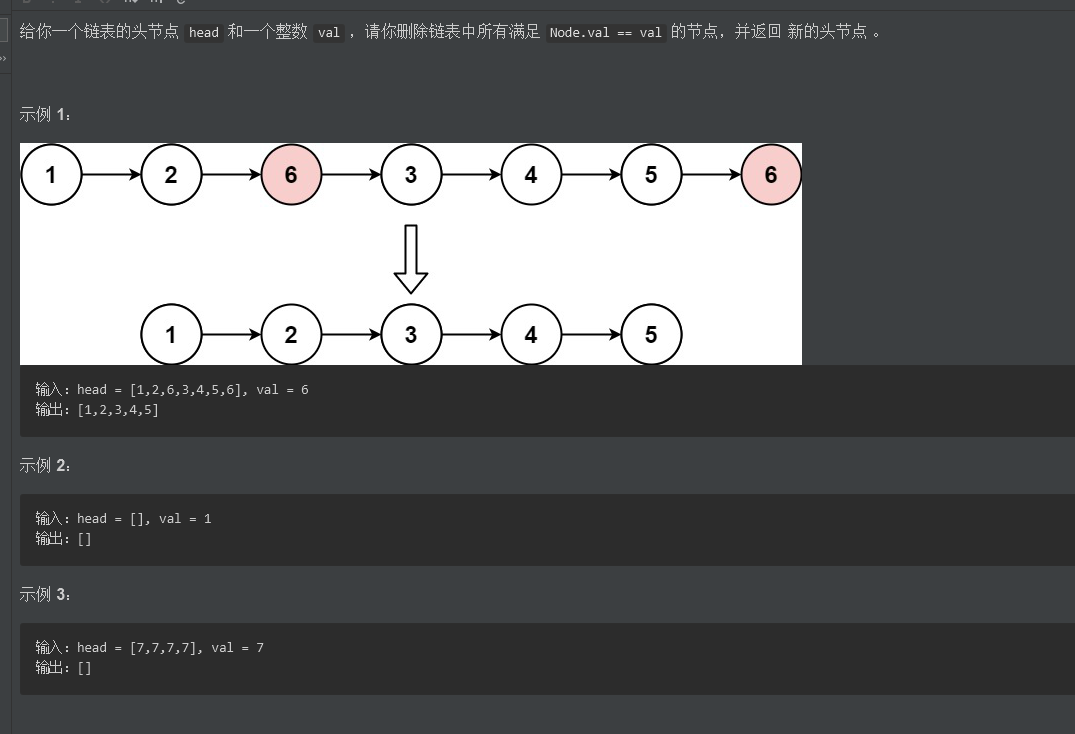
这里呢我们先尝试下对链表进行普通的遍历去解决该问题，之后再说递归
链表解决
那么解决该问题有两种方法，就和我们当时去解决删除链表元素一样，分为带头结点和虚拟头结点两种方式去解决
①带头节点
1、如果是直接从head节点开始，我们说删除元素需要找head的前一个元素，但是head头节点并没有前一个元素，所以如果遇到head的val就是要删除的val时，我们要特殊处理下：
ps:这里和我们写链表删除元素不太相同的是，链表删除元素我们关注的只是删除一个的情况，但是这里是有可能删除多个相同元素的，例如[7,7,7,7]删除完头节点后头节点变为下一个节点时，但此时下一个节点的值还是要删除的元素，所以均需要删除。所以这里不应该是for,而是while。
while (head != null && head.val == val){
head = head.next;
}
//如果删除完头节点或者本来就是空链表时，直接return null;
if(head == null){
return null;
}
2、然后就是处理删除中间元素的情况
那这我们已经轻车熟路了，我们从head开始遍历
通过while循环去找到要删除节点的前一个节点，那么我们这边while的条件就是遍历完整个链表，即只要节点的下一个不为空，就一直遍历下去。
//就正常走删除链表的逻辑即可,从head开始
ListNode pre = head;
while(pre.next != null){
if(pre.next.val == val){
pre.next = pre.next.next;
}else {
pre = pre.next;
}
}
整体代码如下：
public ListNode removeElements(ListNode head, int val) {
//首先如果头结点就是我要删除的元素
while (head != null && head.val == val){
head = head.next;
}
if(head == null){
return null;
}
//就正常走删除链表的逻辑即可,从head开始
ListNode pre = head;
while(pre.next != null){
if(pre.next.val == val){
pre.next = pre.next.next;
}else {
pre = pre.next;
}
}
return head;
}
②虚拟头节点
我们之前学习链表的时候，创建虚拟头节点的原因就是因为我们删除增加节点时，一般要找这个位置的前一个节点，而头节点是没有前面的节点的，所以需要特殊处理，为了将头节点相关操作和增加删除中间元素操作保持一致，我们创建虚拟头结点用来代表头节点的前一个节点。
ListNode dummyHead = new ListNode(-1,head);
那么这样我们可以直接用上面删除中间元素的逻辑了，整体代码如下：
public ListNode removeElements(ListNode head, int val) {
ListNode dummyHead = new ListNode(-1,head);
//就正常走删除链表的逻辑即可,从head开始
ListNode pre = dummyHead;
while(pre.next != null){
if(pre.next.val == val){
pre.next = pre.next.next;
}else {
pre = pre.next;
}
}
return dummyHead.next;
}
在说递归之前，我们来说一下leetCode关于这一类题目我们平常自己调试怎么调试，因为我们知道题目给的ListNode一来不是我们自己定义的结构，而且像题目是直接给你一个完整的链表示例，如果单靠ListNode现在的结构对于我们直接来说是几乎不可能调试的。
所以我们需要增加方法来方便我们调试，例如我们可以直接按照题目示例创建一个数组，然后用数组转化为ListNode:
以本题的为例，例如我想使用以下输入调试：
那么我们可以先创建一个数组，数组元素就是题目中链表的元素：
public static void main(String[] args) {
int[] nums = new int[]{1,2,6,3,4,5,6};
}
然后我们可以将官方给的ListNode的示例类进行改造，我们增加一个通过数组构造ListNode的构造方法：
其实很简单，首先给该节点用数组的第一个元素赋值
然后遍历数组，将数组剩余元素赋值给该链表后面的节点。最后返回当前ListNode节点对象即可。
public ListNode(int[] nums){
if(nums == null || nums.length == 0){
throw new IllegalArgumentException("arr cannot be null");
}
this.val = nums[0];
ListNode cur = this;
for (int i = 1; i < nums.length; i++) {
cur.next = new ListNode(nums[i]);
cur = cur.next;
}
}
然后为了方便我们查看结果，我们可以重写一个toString()方便我们查看结果：
@Override
public String toString(){
StringBuilder stringBuilder = new StringBuilder();
ListNode cur = this;
while (cur != null){
stringBuilder.append(cur.val + "->");
cur = cur.next;
}
stringBuilder.append("NULL");
return stringBuilder.toString();
}
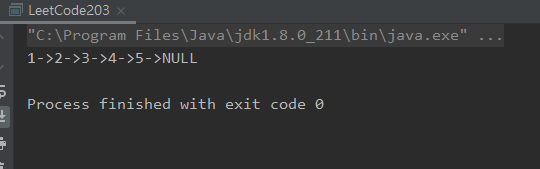
最后我们实践一下：
public static void main(String[] args) {
int[] nums = new int[]{1,2,6,3,4,5,6};
ListNode listNode = new ListNode(nums);
System.out.println(removeElements(listNode,6).toString());
}
三、递归
3.1、递归定义和递归的宏观语意
- 本质上，递归就是将原来的问题，转化为更小的同一问题，通常是小到不能再小，此时我们可以很容易的解决这道问题。
- 举例：数组求和
①定义Sum(arr[0…n-1]) 我们可以将其转化为 arr[0] + Sum(arr[1…n-1])
那么大家就能很轻松的看到后一个Sum函数解决的问题比前一个Sum函数解决的问题就要小一些。前一个函数要对n个元素求和，后一个Sum函数只需要对n-1个元素求和。
②那么依次类推，我要求索引1到n-1这些元素之和又可以转化为arr[1]+Sum(arr[2…n-2])…
③直到最后，我这个问题逐渐缩小，Sum变成只需要求n-1这一个元素之和，那么此时Sum(arr[n-1…n-1]) = arr[n-1] +Sum([])，此时空数组没有值了，此时Sum函数值就是0，该问题变转化为最基本的问题，就很容易解决该问题了。
那么下面我们可以按照上面思路来实践下递归数组求和：
public static int sum(int[] arr){
return sum(arr,0);
}
private static int sum(int[] arr,int l){
//首先最基本的问题，就是当左边界等于数组长度的时候(sum(n-1..n-1)),此时就是arr[n-1] + sum({}),而sum({})就对应最基本的问题，此时结果是0
if(l == arr.length){
return 0;
}
//然后就是每一步的拆解，将问题简化为最左边界对应的数组元素加上这元素之后的和，我们就可以使用递归解决了
return arr[l] + sum(arr,l+1);
}
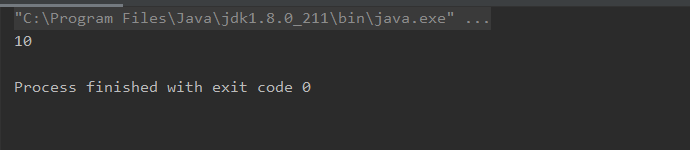
我们测试一下：
public static int sum(int[] arr){
return sum(arr,0);
}
结果得到是10：
所以递归难在我们如何将原问题转化为更小的相同类型问题，所谓的转化不是求一个更小的问题的答案就行了，而是我们要根据这个更小问题的答案构建出原问题的答案。例如这里的构建就是arr[l]+sum(arr,l+1)，其实就是一个累加的过程，这是一个典型的分而治之的思想，将问题逐渐减小，直到达到基本情况。
而转化的过程，我们一定要注意递归函数本身的语义，例如刚才这道题，sum函数本身就是计算arr[l…n-1]范围里的数字和，这里我们将其称为递归函数的"宏观"语意。
那么在这样一个语义下，我们设计转化逻辑的时候，可以尝试着抛弃掉我在设计递归算法这样的念头，不要去想我是怎样递归调用的，因为这很有可能会把你绕进去，而是回归到语义本身。因为递归函数本身也是一个函数，它就是为了完成一个功能。它本质就像一个函数A里头调用子函数B，只不过现在把B换成了A，没什么区别。
例如对于sum(int[] arr,int l)这个函数来说，你不要想你是在写递归，你就把它看成一个我要计算从数组索引l到n这么一个求和的函数，同时我有一个sum的子函数，要用上它，那么我们自然就可以想到那我就把它转化成arr[l] + sum(arr,l+1),用上了子函数sum，得到这个结果就好了。我们就是用子函数来构建逻辑去解决上层函数的问题，这样去想或许能够帮助我们去正确的写出递归函数。
3.2、用递归解决链表相关问题
对于一个链表来说，我们可以把它转化成如下形式：
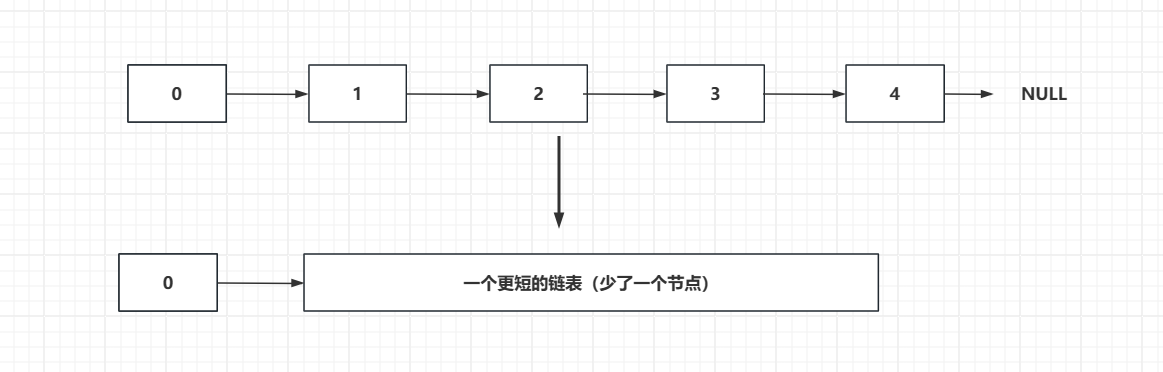
即链表本身我们可以理解为一个一个节点的挂接又可以把它看作是一个头节点后面接了一个更短的链表，直至最后，我们可以把NULL看作最基本的链表。这也是为什么我们说链表具有天然的递归性。
那么我们拿之前LeetCode的题目为例，我们同样可以利用链表的递归性去解决，思路如下：
首先我们找到最基本的问题，很简单，就是当这个链表是NULL的时候，我们直接返回NULL即可
然后就是将大问题转化成小问题，我们可以将链表看作是头节点挂接着一个更小的链表，那么我们就可以利用递归了。但是递归归递归，我们把这个函数看作是一个子函数的情况，如何去真正解决删除元素这个原本的问题呢？
那么当我们拆解成头节点和一个更短的链表的时候
通过去判断head的val是否等于我们要删除的val
如果等于，直接返回这个更短的链表，如果不等于，保留head,直接head.next = 更短的链表,然后return head即可。这样我们才算回归到了问题本身，才能解决删除链表元素的问题。代码如下：
public static ListNode removeElements3(ListNode head, int val) {
if(head == null){
return null;
}
ListNode res = removeElements3(head.next, val);
if(head.val == val){
return res;
}else {
head.next = res;
return head;
}
}
那么上述代码我们可以优化一下，我们直接用head.next去装递归函数的结果。
public ListNode removeElements(ListNode head, int val) {
if (head == null) {
return null;
}
head.next = removeElements(head.next, val);
return head.val == val ? head.next : head;
}
可以看到递归写法使我们的代码非常的整洁简短。
执行结果如图所示：
虽然说注重递归的宏观语义对于我们帮助理解递归是很好的方法，但是可能很多小伙伴和我一开始一样，并没有看到链表相关的删除节点操作，不理解为什么这样写就能删除节点了，那么下面我们就通过上面说的数组之和与力扣203这两个例子去深入剖析递归的内部机制
3.3、递归函数的“微观”解读
我们之前学习栈的时候，曾经说到过系统栈这样一个应用，在一个函数中调用子函数时，这个子函数的位置会被压入一个系统栈，当子函数调用完成后，就会从系统栈中出栈找到上次子函数调用的位置从而继续执行主函数。
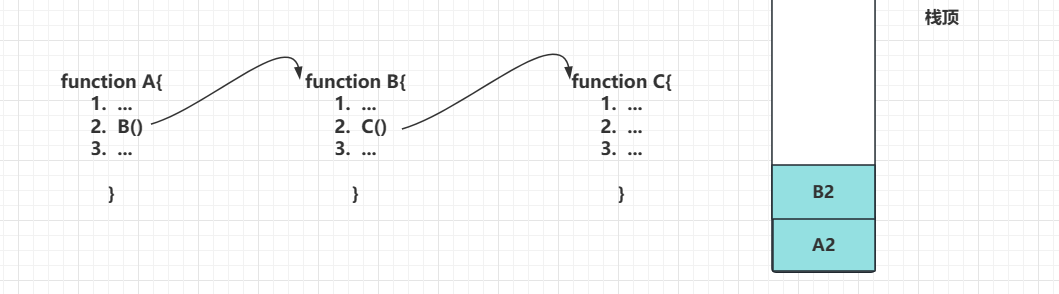
而我们之前也说过，递归也其实类似这种调用，只不过将子函数换做了主函数本身而已。
例如之前通过递归解决数组之和的例子：
private static int sum(int[] arr, int l) {
if (l == arr.length) {
return 0;
}
return arr[l] + sum(arr, l + 1);
}
我们可以将上面代码作如下拆分：
private static int sum(int[] arr, int l) {
if (l == arr.length) {
return 0;
}
int x = sum(arr, l + 1); //将递归函数获取的结果通过x暂存
int res = arr[l] + x; //然后用最左边界数组值和x求和通过res暂存
return res;
}
递归函数的调用，本质就是函数调用
我们看一下上面拆分后的函数到底是如何递归调用的：
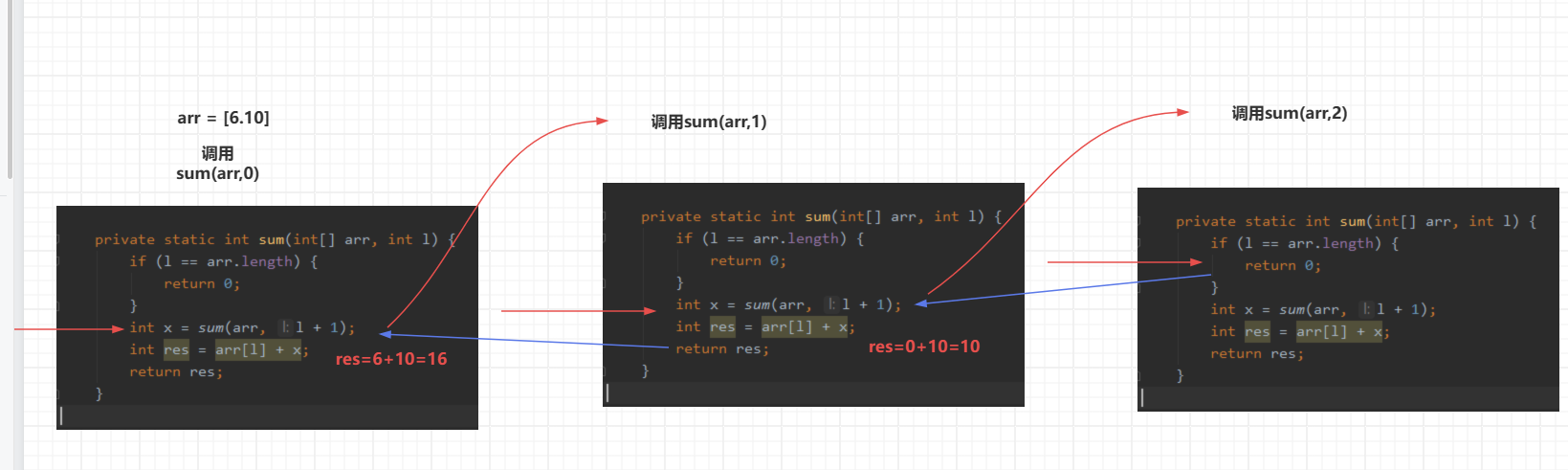
得到16后，主函数执行完毕，无其他需要执行的子函数，所以返回16，主函数执行完毕。
我们接下来看一下LeetCode203这道题的递归调用：
public static ListNode removeElements3(ListNode head, int val) {
if (head == null) {
return null;
}
head.next = removeElements3(head.next, val);
return head.val == val ? head.next : head;
}
以上我们通过两个例子演示了具体的栈调用的过程，其实就是上面的栈的子函数调用，这个子函数仍然是主函数本身。
但也正因为栈的子函数调用这个原理本身，递归调用我们也能知道是有代价的，那就是函数调用需要的更多时间以及系统栈空间额外的空间开销。所以当栈空间占满的时候，此时递归就会出现问题。例如上面数组求和，当你的数组是一个百万级别的数组，那么用递归就会导致你的递归调用很可能SOF栈内存溢出。
但是递归调用本身的好处就是代码更加整洁，逻辑会变得更加简单。这种特性在非线性数据结构会凸显的更加明显。
3.4、链表CRUD改为递归
大家感兴趣的话可以自行将之前链表的CRUD操作改为递归方法，这样可以提升你对递归的掌握，这里我在下面贴出我链表的CRUD的递归实现：
import javafx.util.Pair;
public class LinkedList<T> {
//只有在链表结构内才能访问Node,链表结构外用户无法访问，因为对于用户而言，他们不需要指定链表的底层实现
private class Node {
public T data;
public Node next;
public Node(T data, Node next) {
this.data = data;
this.next = next;
}
public Node(T data) {
this(data, null);
}
public Node() {
this(null, null);
}
@Override
public String toString() {
return data.toString();
}
}
private Node dummyHead;
private int size;
public LinkedList() {
dummyHead = new Node(null, null);
this.size = 0;
}
public int getSize() {
return size;
}
public boolean isEmpty() {
return size == 0;
}
//在链表的Index(0-based)位置添加新的元素e
public void add(T t, int index) {
if (index < 0 || index > size) {
throw new IllegalArgumentException("add element error:index should >= 0 && index <= size");
}
Node prev = dummyHead;
for (int i = 0; i < index; i++) {
prev = prev.next;
}
Node node = new Node(t);
node.next = prev.next;
prev.next = node;
size++;
}
public void add2(T t, int index) {
if (index < 0 || index > size) {
throw new IllegalArgumentException("add element error:index should >= 0 && index <= size");
}
dummyHead.next = addRecursion(dummyHead.next, t, index);
size++;
}
public Node addRecursion(Node node, T t, int index) {
if (index == 0) {
return new Node(t, node);
}
node.next = addRecursion(node.next, t, --index);
return node;
}
public void addFirst(T t) {
//声明一个新的节点，将这个新节点指向我们的头结点，然后再让新的节点成为头结点
add2(t, 0);
}
public void addLast(T t) {
add2(t, size);
}
//获取index索引上的元素
public T get(int index) {
if (index < 0 || index >= size) {
throw new IllegalArgumentException("get failed;index should >= 0 or index < size");
}
Node cur = dummyHead.next;
for (int i = 0; i < index; i++) {
cur = cur.next;
}
return cur.data;
}
//获取index索引上的元素
public T get2(int index) {
if (index < 0 || index >= size) {
throw new IllegalArgumentException("get failed;index should >= 0 or index < size");
}
Node node = getRecursion(dummyHead.next, index);
return node.data;
}
private Node getRecursion(Node node, int index) {
if (index == 0) {
return node;
}
return getRecursion(node.next, --index);
}
public boolean contains(T t) {
Node cur = dummyHead.next;
while (cur != null) {
if (cur.data == t) {
return true;
}
cur = cur.next;
}
return false;
}
public boolean contains2(T t) {
return containsRecursion(dummyHead.next, t);
}
public boolean containsRecursion(Node node, T t) {
if (node == null) {
return false;
}
if (node.data.equals(t)) {
return true;
}
return containsRecursion(node.next, t);
}
public T getFirst() {
return get2(0);
}
public T getLast() {
return get2(size - 1);
}
public void set(int index, T t) {
if (index < 0 || index >= size) {
throw new IllegalArgumentException("get failed;index should >= 0 or index < size");
}
Node cur = dummyHead.next;
for (int i = 0; i < index; i++) {
cur = cur.next;
}
cur.data = t;
}
public void set2(int index, T t) {
if (index < 0 || index >= size) {
throw new IllegalArgumentException("get failed;index should >= 0 or index < size");
}
setRecursion(dummyHead.next,index,t);
}
private void setRecursion(Node node, int index, T t) {
if(index == 0){
node.data = t;
return;
}
setRecursion(node.next,--index,t);
}
public T remove(int index) {
if (index < 0 || index >= size) {
throw new IllegalArgumentException("get failed;index should >= 0 or index < size");
}
Node prev = dummyHead;
for (int i = 0; i < index; i++) {
prev = prev.next;
}
Node ret = prev.next;
prev.next = ret.next;
ret.next = null;
size--;
return ret.data;
}
public T remove2(int index) {
if (index < 0 || index >= size) {
throw new IllegalArgumentException("get failed;index should >= 0 or index < size");
}
Pair<Node, T> pair = removeRecursion(dummyHead.next, index);
dummyHead.next = pair.getKey();
size--;
return pair.getValue();
}
private Pair<Node,T> removeRecursion(Node node, int index) {
if(index == 0){
//返回当前要删除的节点的下一个节点和它的值
return new Pair<>(node.next,node.data);
}
Pair<Node, T> res = removeRecursion(node.next, --index);
node.next = res.getKey();
return new Pair<>(node,res.getValue());
}
public T removeFirst() {
return remove2(0);
}
public T removeLast() {
return remove2(size - 1);
}
@Override
public String toString() {
StringBuilder stringBuilder = new StringBuilder();
Node cur = dummyHead.next;
while (cur != null) {
stringBuilder.append(cur + "->");
cur = cur.next;
}
stringBuilder.append("NULL");
return stringBuilder.toString();
}
public static void main(String[] args) {
LinkedList<Integer> integerLinkedList = new LinkedList<>();
for (int i = 0; i < 5; i++) {
integerLinkedList.addFirst(i);
System.out.println(integerLinkedList);
}
integerLinkedList.add2(666, 2);
System.out.println(integerLinkedList);
System.out.println(integerLinkedList.get2(3));
integerLinkedList.set2(3,114514);
System.out.println(integerLinkedList.get2(3));
System.out.println(integerLinkedList.contains2(666));
System.out.println(integerLinkedList);
System.out.println(integerLinkedList.remove2(2));
System.out.println(integerLinkedList.removeLast());
System.out.println(integerLinkedList);
}
}
其中xxx2的方法都是CRUD调用递归的主方法，而xxxRecursion()则是被调用的递归方法。
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码（1）
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 【C语言】——认识指针变量和地址，以及指针变量类型的意义
- BAPI_PO_CREATE1 创建的采购订单为何是PBXX，而不是PB00的代码
- 【【C++11特性篇】【强制/禁止 】生成默认函数的关键字default＆delete（代码演示）
- 大数据、知识图谱和强化学习的综合应用
- 【12.30】转行小白历险记-刷算法06
- C++ STL vector容器详解
- 什么是机器学习?
- 制造行业定制软件解决方案——工业信息采集平台
- 开关电源知识分享与总结
- 【解决】IntelliJ IDEA 重命名 Shift + F6 失效