【leetcode 2171. 拿出最少数目的魔法豆】没有数学，全是思路

2171. 拿出最少数目的魔法豆

题目描述

给定一个 正整数 数组 beans ，其中每个整数表示一个袋子里装的魔法豆的数目。

请你从每个袋子中 拿出 一些豆子（也可以 不拿出），使得剩下的 非空 袋子中（即 至少还有一颗 魔法豆的袋子）魔法豆的数目 相等。一旦把魔法豆从袋子中取出，你不能再将它放到任何袋子中。

请返回你需要拿出魔法豆的 最少数目。

如果读者已经看了官方题解，会发现是通过一系列数学推理得出一个数学公式，最后利用公式写代码。

这对看到数学公式就头疼星人不太友好，这边文章就是通过笔者3次提交，还原出如何不用数学公式推理出和官方题解一样的结果。

第一次提交——简单但正确的思路

在题目描述中，有一个条件增大了题目难度：

使得剩下的 非空 袋子中（即 至少还有一颗 魔法豆的袋子）魔法豆的数目 相等。

如果没有非空的要求，这个题目其实就是一个简单的计算题，只需要找到豆子最少的袋子，然后把其他袋子中多余的豆子拿出去，最后计算拿出去的总量即可。

增加了非空的要求，其实就有了变动的空间。像[1,10,11]，如果没有非空要求，答案是19，加上非空要求，就可以通过把第一个袋子清空，再对后面两个袋子运用上面的过程，就可以减少到1 + 1 = 2。

要解决非空条件带来的变化，思路也很简单：分别判断“不清空任何袋子”，“清空1个袋子”，“清空2个袋子”…，直到只剩下一个袋子，从所有结果中，找到最小的即可，当然要从豆子数量最小的开始清空。

所以，最终思路是：

• 对所有袋子按照豆子数量，升序排序
• 从豆子最少的袋子开始，
  • 不清空任何袋子，按照无非空条件的情况计算配平所有袋子需要拿出的豆子数目
  • 清空豆子最少的袋子，对剩余袋子按照无非空条件的情况计算配平所有袋子需要拿出的豆子数目
  • 清空豆子最少的两个袋子，对剩余袋子按照无非空条件的情况计算配平所有袋子需要拿出的豆子数目
  • ……
  • 清空除豆子最多的两个袋子外的所有袋子，对这两个袋子按照无非空条件的情况计算配平所有袋子需要拿出的豆子数目
• 上述结果中的最小值就是我们需要的最终结果

根据上面的思路，容易写出如下C++代码：

class Solution {
public:
    long long minimumRemoval(vector<int>& beans) {
        // 1. 根据豆子数量，对袋子升序排序
        // 2. 从最小的袋子的开始清空
        // 3. 从清空0个开始，计算需要拿出的豆子
        int len = beans.size();
        sort(beans.begin(), beans.end()); // 升序排序
        
        long long res = -1;
        for(int i = 0;i < len;++i) {
            long long tmp = 0;
            // 计算清空前面小袋子需要拿出的豆子总数
            for(int j = 0;j < i;++j) {
                tmp += beans[j];
            }
            // 计算配平所有袋子需要拿出的袋子数量
            for(int j = i + 1;j < len;++j) {
                tmp += (beans[j] - beans[i]);
            }
            if(res < 0) {
                res = tmp;
            } else {
                res = min(res, tmp);
            }
        }
        return res; 
    }
};

提交后，发现会超时：

第二次提交——空间换时间，不再超时

现在我们可以思考一下，上面代码中有没有重复计算，是否可以优化其性能。

上述代码的循环中，主要有两个计算：

1. 计算清空前面i个袋子需要拿出的豆子数量
2. 计算配平后面len - i个袋子，需要拿出的豆子数量

第1个计算，可以用前缀和，在一个循环中计算，并记录下来。

对于第2个计算，所谓配平len - i个袋子，其实就是把[i + 1, i + 2, ..., len -1]袋子中多余的豆子拿出。

配平这些袋子需要拿出的豆子数就是图中红色部分：

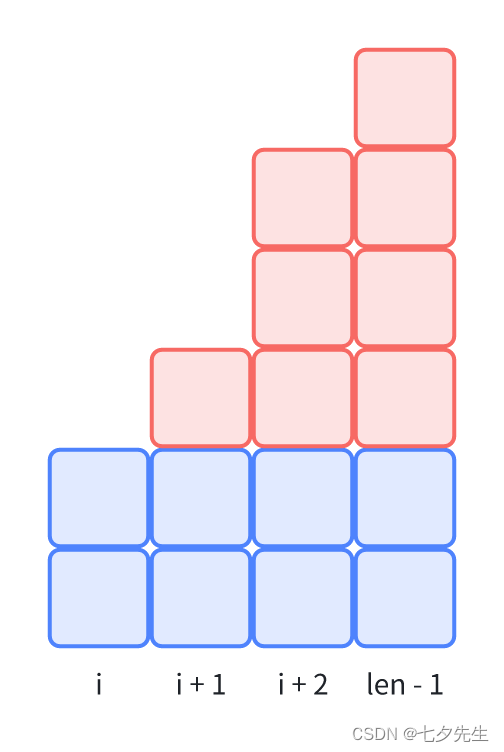
可以直接计算出来：
假设：

• 配平$i$到$len?1$袋子需要拿出的豆子数为$righ{t}_i$
• 所有豆子总数为$sum$
• 前$i$个袋子中豆子总数为$left\_su{m}_i$

那么$i$到$len?1$袋子中豆子总数，也就是上图中所有方块的数目为$right\_su{m}_i=sum?left\_su{m}_i$

配平$i$到$len?1$袋子需要拿出的豆子数，也就是图中红色部分 = 图中总方块数 - 蓝色部分，既$righ{t}_i=right\_su{m}_i?(len?i)\times beans[i]$

这样我们就可以提前计算1和2，那么在循环中就可以不再重复计算，对应的C++代码如下：

class Solution {
public:
    long long minimumRemoval(vector<int>& beans) {
        // 1. 根据豆子数量，对袋子升序排序
        // 2. 从最小的袋子的开始清空
        // 3. 从清空0个开始，计算需要拿出的豆子
        int len = beans.size();
        sort(beans.begin(), beans.end()); // 升序排序
        long long bean_sum = accumulate(beans.begin(), beans.end(), (long long)0); // 所有袋子中豆子总量

        vector<long long> left_sum(len + 1, 0); // 前i个袋子中豆子的总数
        for(int i = 1;i <= len;++i) {
            left_sum[i] = left_sum[i - 1] + beans[i - 1];
        }

        vector<long long> right(len, 0); // 配平i到len - 1袋子，需要拿出的豆子数量
        for(int i = 0;i < len;++i) {
            // 配平i到len - 1袋子需要拿出的豆子数 = 豆子总数 - 前面i个袋子中豆子总数 - 后面i到len - 1个袋子配平后的袋子总量
            right[i] = bean_sum - left_sum[i] - (len - i) * (long long)beans[i];
        }
        
        long long res = bean_sum;
        for(int i = 0;i < len;++i) {
            long long tmp = left_sum[i] + right[i];
            res = min(res, tmp);
        }
        return res; 
    }
};

这次提交已经可以成功通过了。

第三次提交——发现规律，简化代码

仔细观察上面代码，会发现计算right[i]时减去的left_sum[i]到循环阶段计算tmp的时候又加回去了。

也就是说第1个计算是多余的。

去掉第1个left_sum的计算，后面两个循环其实可以合并起来了，最终变成了和官方解法一样的结构，C++实现如下。

class Solution {
public:
    long long minimumRemoval(vector<int>& beans) {
        int len = beans.size();
        sort(beans.begin(), beans.end()); // 升序排序
        long long bean_sum = accumulate(beans.begin(), beans.end(), (long long)0); // 所有袋子中豆子总量

        long long res = bean_sum;
        for(int i = 0;i < len;++i) {
            res = min(res,bean_sum -  (len - i) * (long long)beans[i]);
        }
        
        return res; 
    }
};

结果还不错