代码随想录Day.31 | 455. 分发饼干、376. 摆动序列、53. 最大子序和

455. 分发饼干

1. LeetCode链接

455. 分发饼干 - 力扣（LeetCode）

2. 题目描述

3. 解法

????????贪心法，首先想到的是，局部最优：让每个孩子尽可能拿能拿到的最小饼干尺寸。为了方便查找，这就要求至少饼干尺寸是从小到大排列的。

? ? ? ? 两个for循环解决。把小孩按照胃口也从小到大排列更快。

class Solution {
public:
    int findContentChildren(vector<int>& g, vector<int>& s) {
        vector<bool> used(s.size(), false);
        int sum = 0;
        // sort(g.begin(), g.end());
        sort(s.begin(), s.end());
        for (int i = 0; i < g.size(); i++) {
            for (int j = 0; j < s.size(); j++) {
                if (used[j]) continue;
                if (s[j] >= g[i]) {
                    sum++;
                    used[j] = true;
                    break;
                }
            }
        }
        return sum;
    }
};

但是很明显，还是太慢了。

????????假如说，小孩的胃口和饼干的尺寸都从小到大排序。可以着么想。加入某个小孩i和某个饼干j匹配成功了，后面一个小孩i+1就只能去匹配后面的饼干(> j)，前面的饼干完全不需要考虑。所以只用一个for循环就可以搞定。

? ? ? ??

class Solution {
public:
    int findContentChildren(vector<int>& g, vector<int>& s) {
        sort(g.begin(), g.end());
        sort(s.begin(), s.end());
        int index = 0;
        for (int i = 0; i < s.size() && index < g.size(); i++) {
            if (g[index] <= s[i]) {
                index++;
            }
        }
        return index;
    }
};

其中，for循环时由饼干的数组控制的，原因在于，如果当前小孩和饼干不匹配的话，即当前饼干不是能满足小孩的最小尺寸饼干，应该用下一块饼干去匹配当前小孩。

假如用，下一个小孩去匹配当前饼干，而在当前小孩都不匹配的情况下，下一个胃口更大的小孩更不可能匹配，这就导致在一个for循环下，找不到任何一对匹配的。

376. 摆动序列

1. LeetCode链接

376. 摆动序列 - 力扣（LeetCode）

2. 题目描述

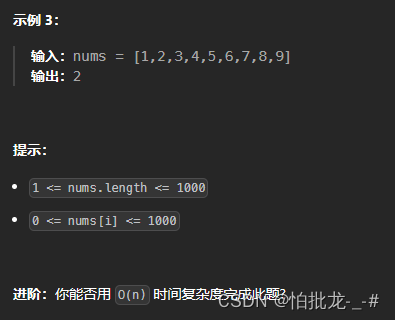
3. 解法

贪心，局部最优：每次找最近的一对相邻的数字，且两数之差与上一个不一样。

详细来说，摆动序列要求序列数组成上坡——下坡交替状。

而一般的数组在一对上下坡之间，要不是有一堆单调坡，要不是有平路。

摆动序列，即找峰值点旁边的上下坡。

代码解读：

????????首先，要找到合适的初值，主要是防止前n项都为相同的值。int cha的作用是记录第一对相邻但不相等的差值。找到初值后，初始化bool turn，turn == true表示前一个差值是正数，否则是负数。

? ? ? ? 找到初值并初始化turn后，接下来就开始找与上一个差值不同的相邻两数，改变turn，如此往复。

class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
        int cha = 0;
        bool turn = true;
        int len = 1;
        for (int i = 1; i < nums.size(); i++) {
            if (cha == 0 && nums[i] - nums[i - 1] != 0) {
                cha = nums[i] - nums[i - 1];
                turn = (cha > 0 ? true : false);
                len++;
            } else {
                if ((nums[i] - nums[i - 1] > 0 && turn == false) || (nums[i] - nums[i - 1] < 0 && turn == true)) {
                    len++;
                    turn = (turn == true ? false : true);
                }
            }

        }
        return len;
    }
};

53. 最大子数组和

1. LeetCode链接

53. 最大子数组和 - 力扣（LeetCode）

2. 题目描述

3. 解法

1. 我的解法

? ? ? ? 首先考虑特殊情况，即数组中全是非正数，这就成了找最大值的题。

? ? ? ? 需要遍历一遍，遍历完就输出最大值，遇到第一个正数则停止。

? ? ? ? 将第一个正数累加到sum上。

????????从一个正数的下一个开始开始，遇到下一个正数结束，为一个阶段。有两种情况：1. 该阶段中的负数累加到sum上后的值<0，则刷新累加和sum，和局部累加和sumb。此种情况要记录之前最大的sum；2. sumb>0，则sumb加到累加和上，sumb刷新。

比较之前记录的历史最大sum和当前的sum，输出较大的一个。

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int sum = INT_MIN;
        int i = 0;
        for (; i < nums.size(); i++) {
            if (nums[i] > 0) break;
            else if (nums[i] > sum) sum = nums[i];
        }
        if (i == nums.size()) return sum;
        sum = nums[i];
        i++;
        int sumb = 0;
        int max = INT_MIN;
        for (; i < nums.size(); i++) {
            if (sum + sumb < 0) {
                if (sum > nums[i] && sum > max) max = sum; 
                sum = 0;
                sumb = 0;
            }
            sumb += nums[i];
            if (sumb > 0) {
                sum += sumb;
                sumb = 0;
            }
        }
        return sum > max ? sum : max;
    }
};

1. 记录所有可能的连续和为正值的和，只保留最大值。

2. 改变连续子区间的起点和终点，在子区间累加和<0后，使子区间累加和=0，相当于重新设置起点；重点是使得累加和>=0的所有，都可以成为终点，保留最大子区间和。

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int result = INT32_MIN;
        int count = 0;
        for (int i = 0; i < nums.size(); i++) {
            count += nums[i];
            if (count > result) { // 取区间累计的最大值（相当于不断确定最大子序终止位置）
                result = count;
            }
            if (count <= 0) count = 0; // 相当于重置最大子序起始位置，因为遇到负数一定是拉低总和
        }
        return result;
    }
};