统计1亿以内素数的个数，要求运行时间小于1秒

看到这个题目，首先想到欧拉筛选素数法。

欧拉筛选素数法的原理是从2开始，留下2，把2的倍数剔除掉，然后，留下3，把3的倍数剔除掉，再把下一个没有被剔除的数作为素数留下，再把它的倍数剔除掉，以此类推，直到最后一个数。在整个剔除过程中，留下的都是素数。

依据欧拉筛选法编写程序如下：

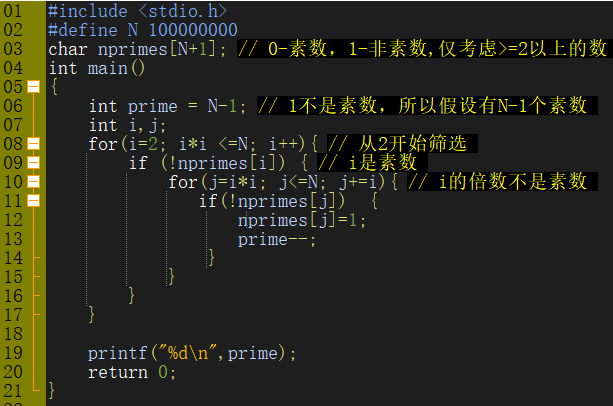
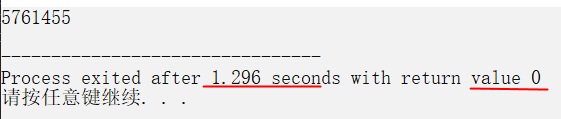
程序运行结果如下图所示，超过1s，不能满足题目要求。下面对该程序进行优化。

优化后的程序如下：

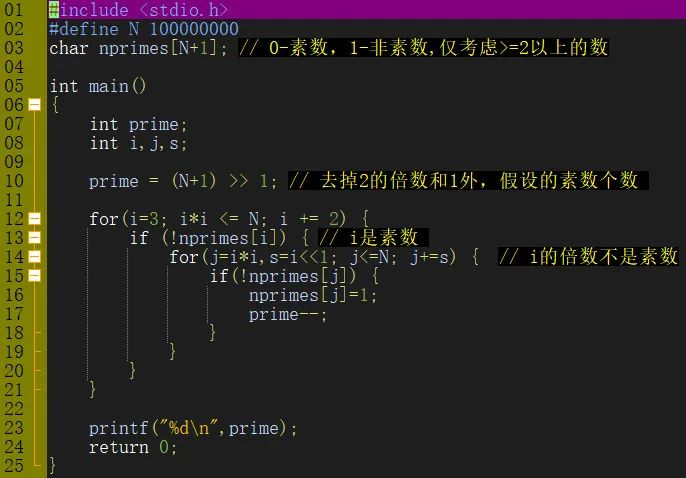
程序运行结果如下图所示，满足了题目的要求。

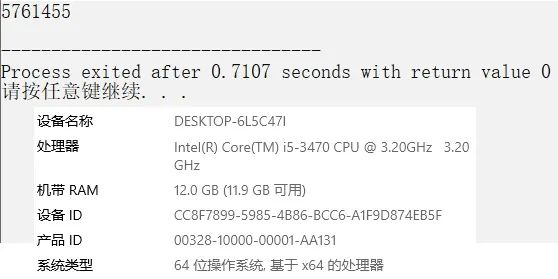
另外，在网上看到一个更好的程序，也使用的是筛选法，但优化了很多，感兴趣的读者可参看[1]。程序如下：

#include <time.h>
#include <stdio.h>
#define N 100000000
#define size (N/6*2 + (N%6 == 5? 2: (N%6>0)))
int p[size / 32 + 1] = {1};
int creat_prime(void)
{
  int i, j;
  int len, stp;
  int c = size + 1;
  for (i = 1; ((i&~1)<<1) * ((i&~1) + (i>>1) + 1) < size; i++)
  {
    if (p[i >> 5] >> (i & 31) & 1) continue;
    len = (i & 1)? ((i&~1)<<1) + 3: ((i&~1)<<2) + 1;
    stp = ((i&~1)<<1) + ((i&~1)<<2) + ((i & 1)? 10: 2);
    j = ((i&~1)<<1) * (((i&~1)>>1) + (i&~1) + 1) + ((i & 1)? ((i&~1)<<3) + 8 + len: len);
    for (; j < size; j += stp)
    {
      if (p[j >> 5] >> (j & 31) & 1 ^ 1)
        p[j >> 5] |= 1L << (j & 31), --c;
      if (p[(j-len) >> 5] >> ((j-len) & 31) & 1 ^ 1)
        p[(j-len) >> 5] |= 1L << ((j-len) & 31), --c;
    }
    if (j - len < size && (p[(j-len) >> 5] >> ((j-len) & 31) & 1 ^ 1))
      p[(j-len) >> 5] |= 1L << ((j-len) & 31), --c;
  }
  return c;
}
int main( )
{
  printf("%d ", creat_prime());
}

运行结果如下图所示，仅仅用了0.3s。

参考资料

[1]https://www.dounaite.com/article/62713ec3725cc324206b6671.html

[2]李红卫，李秉璋.?C程序设计与训练（第四版）[M]，大连，大连理工大学出版社，2023.

[3]https://pan.baidu.com/s/17ZXphwqySNIsIgcGtYMjvg?pwd=lhwc