每日一题:LCR 095.最长公共子序列(DP)
发布时间:2023年12月24日
题目描述:
给定两个字符串?text1?和?text2,返回这两个字符串的最长?公共子序列?的长度。如果不存在?公共子序列?,返回?0?。
一个字符串的?子序列?是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
- 例如,
"ace"?是?"abcde"?的子序列,但?"aec"?不是?"abcde"?的子序列。
两个字符串的?公共子序列?是这两个字符串所共同拥有的子序列。
示例 1:
输入:text1 = "abcde", text2 = "ace" 输出:3 解释:最长公共子序列是 "ace" ,它的长度为 3 。
示例 2:
输入:text1 = "abc", text2 = "abc" 输出:3 解释:最长公共子序列是 "abc" ,它的长度为 3 。
示例 3:
输入:text1 = "abc", text2 = "def" 输出:0 解释:两个字符串没有公共子序列,返回 0 。
提示:
1 <= text1.length, text2.length <= 1000text1?和?text2?仅由小写英文字符组成。
思路:
本题采用动态规划的思想,是一道很经典的动态规划问题,我们把查找公共子序列问题一步一步压缩成最小子问题。创建dp表,写出状态转移方程,本题难点在于如何求出状态转移方程。
首先,第一种情况当最后一个字符相同时,我们只要比较前n-1个字符,第二种情况,当最后一个字符不同时,我们将一个字符串的最后一位相前移动一个比较。
如图:
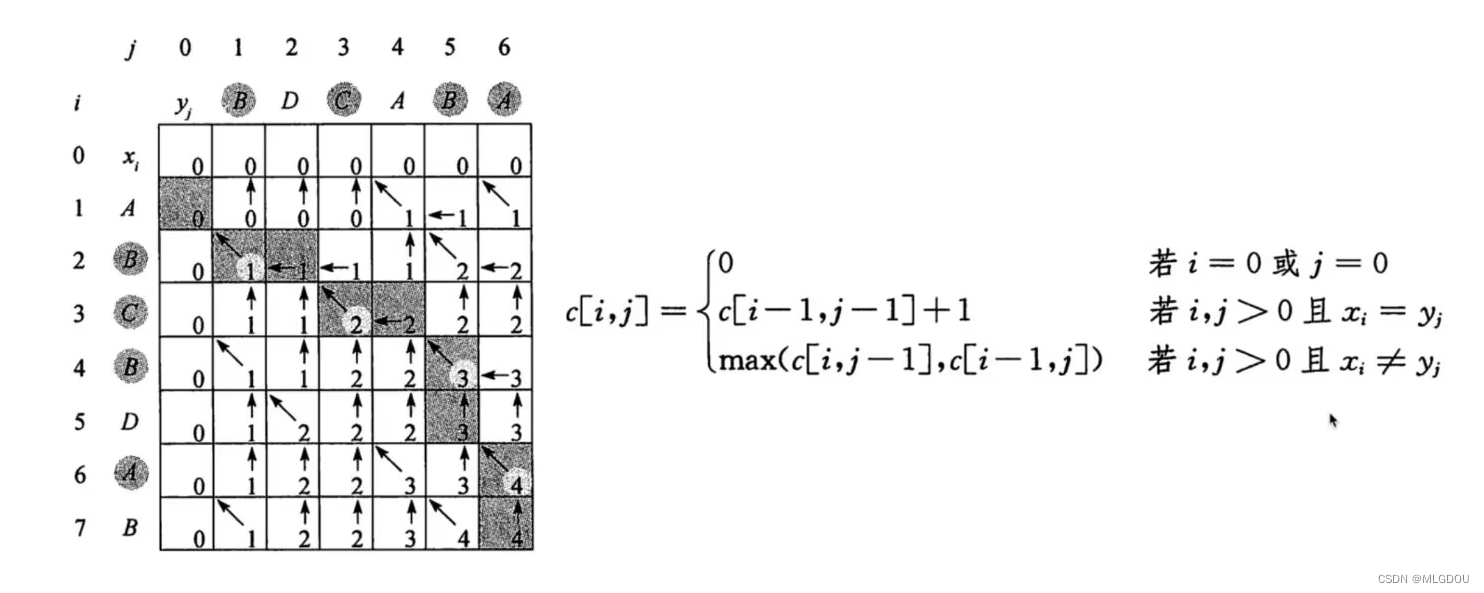
然后代码实现时注意细节:我们dp表要创建的是m+1和n+1的大小,好进行初始化。
代码实现
class Solution {
public:
int longestCommonSubsequence(string text1, string text2) {
int m=text1.size();
int n=text2.size();
vector<vector<int>> dp(m+1,vector<int>(n+1,0));
for(int i=1;i<m+1;i++)
{
for(int j=1;j<n+1;j++)
{
if(text1[i-1]==text2[j-1])
dp[i][j]=dp[i-1][j-1]+1;
else
dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
}
}
return dp[m][n];
}
};
文章来源:https://blog.csdn.net/m0_73865858/article/details/135182036
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- BMP图像文件头
- Luckysheet类似excel的在线表格(vue)
- C //练习 4-6 给计算器程序增加处理变量的命令(提供26个具有单个英文字母变量名的变量很容易)。增加一个变量存放最近打印的值。
- [数据集][目标检测]茶叶病害数据集VOC+YOLO格式883张8类别
- 水利部:加大北斗、无人机等安全监测新技术的应用推广
- Linux Bridge 基本原理
- 超维空间M1无人机使用说明书——21、基于opencv的人脸识别
- 2023 年全国职业院校技能大赛(高职组)“云计算应用”赛项赛卷 B
- OSI七层模型与网络协议
- Docker基本管理