LeetCode 84. 柱状图中最大的矩形
发布时间:2024年01月03日
给定?n?个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
示例 1:
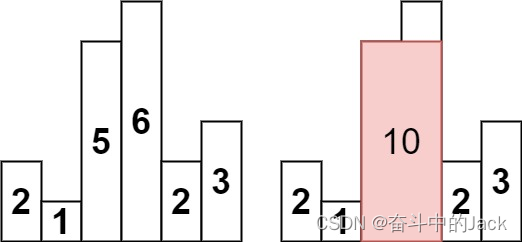
输入:heights = [2,1,5,6,2,3]
输出:10
解释:最大的矩形为图中红色区域,面积为 10
示例 2:

输入: heights = [2,4]
输出: 4
提示:
- 1 <= heights.length <=10^5
- 0 <= heights[i] <= 10^4
解法思路(参考官方题解及视频讲解):
1、暴力1 O(n^3)
for i -> 0, n for j -> i, n (i, j) -> 最小高度,area update max-area2、暴力2 O(n^2)
for i -> 0, n: 找到 left bound, right bound area = height[i] * (right - left) update max-area3、Stack
4、优化 Stack,加哨兵元素
?法一(超时):
class Solution {
public int largestRectangleArea(int[] heights) {
// Time: O(n^3)
// Space: O(1)
int maxArea = 0;
for (int i = 0; i < heights.length; i++) {
for (int j = i; j < heights.length; j++) {
int minHeight = Integer.MAX_VALUE;
for (int k = i; k <= j; k++) {
minHeight = Math.min(minHeight, heights[k]);
}
maxArea = Math.max(maxArea, minHeight * (j - i + 1));
}
}
return maxArea;
}
}法二(超时):
class Solution {
public int largestRectangleArea(int[] heights) {
// Time: O(n^2)
// Space: O(1)
int maxArea = 0;
for (int i = 0; i < heights.length; i++) {
int minHeight = Integer.MAX_VALUE;
for (int j = i; j < heights.length; j++) {
minHeight = Math.min(minHeight, heights[j]);
maxArea = Math.max(maxArea, minHeight * (j - i + 1));
}
}
return maxArea;
}
}法三:
class Solution {
public int largestRectangleArea(int[] heights) {
// Stack 空间换时间
// 特殊情况1:遍历完成后,栈内元素出栈时一定可以扩展到数组的末尾
// 特殊情况2:弹出栈顶后栈为空,一定可以扩散到数组最左边
// 特殊情况3:栈中存在高度相等的元素,出栈
// Time: O(n)
// Space: O(n)
int len = heights.length;
if (len == 0) return 0;
if (len == 1) return heights[0];
int maxArea = 0;
Deque<Integer> stack = new ArrayDeque<>();
for (int i = 0; i < len; i++) {
// 当前元素的高度严格小于栈顶元素的高度时,出栈
while (!stack.isEmpty() && heights[i] < heights[stack.peekLast()]) {
int height = heights[stack.removeLast()];
// 特殊情况3:栈中存在高度相等的元素,出栈
while (!stack.isEmpty() && heights[stack.peekLast()] == height) {
stack.removeLast();
}
// 特殊情况2:弹出栈顶后栈为空,一定可以扩散到数组最左边
int width = stack.isEmpty() ? i : (i - stack.peekLast() - 1);
maxArea = Math.max(maxArea, width * height);
}
stack.addLast(i);
}
// 弹出栈中所有元素
while (!stack.isEmpty()) {
int height = heights[stack.removeLast()];
while (!stack.isEmpty() && heights[stack.peekLast()] == height) {
stack.removeLast();
}
// 特殊情况1:遍历完成后,栈内元素出栈时一定可以扩展到数组的末尾
int width = stack.isEmpty() ? len : (len - stack.peekLast() - 1);
maxArea = Math.max(maxArea, width * height);
}
return maxArea;
}
}
优化法三:
class Solution {
public int largestRectangleArea(int[] heights) {
// Stack(add Sentinel)
// Time: O(N)
// Space: O(N)
int len = heights.length;
if (len == 0) return 0;
if (len == 1) return heights[0];
int maxArea = 0;
int[] newHeights = new int[len + 2];
for (int i = 0; i < len; i++) {
newHeights[i + 1] = heights[i];
}
len += 2;
heights = newHeights;
Deque<Integer> stack = new ArrayDeque<Integer>();
stack.addLast(0);
for (int i = 1; i < len; i++) {
while (heights[stack.peekLast()] > heights[i]) {
int height = heights[stack.removeLast()];
int width = i - stack.peekLast() - 1;
maxArea = Math.max(maxArea, width * height);
}
stack.addLast(i);
}
return maxArea;
}
}
?
文章来源:https://blog.csdn.net/qq_38304915/article/details/135360871
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- MATLAB运行simulink模型显示找不到库Failed to load library
- 关于java的方法重写
- 数据库原理的概述
- 云计算入门——如何选择 Linux 发行版
- 深度解析分布式算法:构建高效稳定的分布式系统
- 【Jmeter】Jmeter基础8-Jmeter元件介绍之断言
- 正向代理和反向代理有什么区别?作为技术你知道吗
- Bind for 0.0.0.0:2379 failed: port is already allocated
- MyBatis-Plus进阶用法详解:打造高效的数据访问层
- 【small syposis: 脾气好的人是怎么做到的?读《非暴力沟通》】