深度学习笔记(六)——网络优化(2):参数更新优化器SGD、SGDM、AdaGrad、RMSProp、Adam
文中程序以Tensorflow-2.6.0为例
部分概念包含笔者个人理解,如有遗漏或错误,欢迎评论或私信指正。
截图和程序部分引用自北京大学机器学习公开课
在前面的博文中已经学习了构建神经网络的基础需求,搭建了一个简单的双层网络结构来实现数据的分类。并且了解了激活函数和损失函数在神经网络中发挥的重要用途,其中,激活函数优化了神经元的输出能力,损失函数优化了反向传播时参数更新的趋势。
我们知道在简单的反馈控制系统中,反馈装置和反馈信号的作用方式都是十分重要的。同样的,在网络反向传播时,只对损失函数进行优化还不够,人们还关注到了执行参数更新时更新的策略。举个例子,如果学习的过程中只有做题和对答案那效果是不够的,只有在对答案的时候同时思考加深自己的理解那样才能达到更好的效果。所以反向传播时,既要优化损失函数,也要优化参数更新的方式。
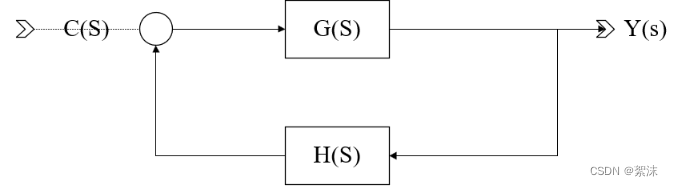
比如上图的结构中反馈值的更新就遵循:
E
(
s
)
=
C
(
s
)
±
Y
(
s
)
×
H
(
s
)
E(s) = C(s) \pm Y(s)\times H(s)
E(s)=C(s)±Y(s)×H(s) 在目前深度学习的研究中已经有很多的优化器被提出。这里主要介绍5种相对简单易于理解的优化器,分别是
SGD、AdaGrad、RMSProp、AdaDelta、Adam
优化器概念
在构建见简单分类网络时构建简单的ML分类器,计算得到损失值后,我们直接用参数减去损失函数梯度。参数更新遵从:
W
t
=
W
t
?
1
?
l
r
?
l
o
s
s
?
W
W_t = W_{t-1} - lr \frac{\partial loss}{\partial W}
Wt?=Wt?1??lr?W?loss?
b
t
=
b
t
?
1
?
l
r
?
l
o
s
s
?
b
b_t = b_{t-1} - lr \frac{\partial loss}{\partial b}
bt?=bt?1??lr?b?loss? 这样的方式符合线性性质,这样难免会使模型在学习复杂的非线性特征时,参数更新存在一定困难。为了优化这个过程,人们考虑到将原来更新参数的部分
?
l
r
?
l
o
s
s
?
b
\ lr \frac{\partial loss}{\partial b}
?lr?b?loss? 进一步提升为两个部分的组合
?
l
r
×
m
t
V
t
\ lr\times \frac{m_t}{\sqrt{V_t} }
?lr×Vt??mt?? 其中mt称之为一阶动量,Vt开方称之为二阶动量。这两个动量可以是损失函数梯度的相关函数或者是损失函数二阶导数的相关函数。我们用nt来代表一阶动量与二阶动量的商。那么参数更新修改为:
η
t
=
l
r
?
m
t
V
t
\eta _t = lr\cdot \frac{m_t}{\sqrt{V_t}}
ηt?=lr?Vt??mt??
W
t
+
1
=
W
t
?
η
t
=
W
t
?
l
r
?
m
t
V
t
W_{t+1} = W_t-\eta _t = W_t - lr\cdot \frac{m_t}{\sqrt{V_t}}
Wt+1?=Wt??ηt?=Wt??lr?Vt??mt??
通过优化器可以引导神经网络通过更好的方式去更新参数。此时参数更新的流程修改为:
- 计算t时刻损失函数对当前参数的梯度 g t = ▽ l o s s = ? l o s s ? W t g_t = \bigtriangledown loss = \frac{\partial loss}{\partial W_t} gt?=▽loss=?Wt??loss?
- 计算t时刻一阶动量m和二阶动量V
- 计算t时刻参数更新的量,即下降的梯度 η t = l r ? m t V t \eta _t = lr\cdot \frac{m_t}{\sqrt{V_t}} ηt?=lr?Vt??mt??
- 计算t+1时刻的新参数
W
t
+
1
=
W
t
?
η
t
=
W
t
?
l
r
?
m
t
V
t
W_{t+1} = W_t-\eta _t = W_t - lr\cdot \frac{m_t}{\sqrt{V_t}}
Wt+1?=Wt??ηt?=Wt??lr?Vt??mt??
在实际的代码中t时刻就是当前算法迭代的总次数。
1、SGD
SGD是最常用的优化器,它的更新方式直接为:
W
t
=
W
t
?
1
?
l
r
?
l
o
s
s
?
W
t
W_t = W_{t-1} - lr \frac{\partial loss}{\partial W_t}
Wt?=Wt?1??lr?Wt??loss? 也就是说在SGD中一阶动量就是损失函数梯度,二阶动量为1。
m
t
=
g
t
=
▽
l
o
s
s
=
?
l
o
s
s
?
W
t
V
t
=
1
m_t = g_t = \bigtriangledown loss = \frac{\partial loss}{\partial W_t} \qquad V_t = 1
mt?=gt?=▽loss=?Wt??loss?Vt?=1
η
t
=
l
r
?
m
t
V
t
=
l
r
?
g
t
\eta _t = lr\cdot \frac{m_t}{\sqrt{V_t}}=lr \cdot g_t
ηt?=lr?Vt??mt??=lr?gt?
这里继续使用之前的分类任务程序构建简单的ML分类器,可以知道SGD更新就是:
# 训练部分
for epoch in range(epoch): #数据集级别的循环,每个epoch循环一次数据集
for step, (x_train, y_train) in enumerate(train_db): #batch级别的循环 ,每个step循环一个batch
with tf.GradientTape() as tape: # with结构记录梯度信息
y = tf.matmul(x_train, w1) + b1 # 神经网络乘加运算
y = tf.nn.softmax(y) # 使输出y符合概率分布(此操作后与独热码同量级,可相减求loss)
y_ = tf.one_hot(y_train, depth=3) # 将标签值转换为独热码格式,方便计算loss和accuracy
loss = tf.reduce_mean(tf.square(y_ - y)) # 采用均方误差损失函数loss = mse = mean(sum(y-out)^2)
loss_all += loss.numpy() # 求loss平均值
# 计算loss对各个参数的梯度
grads = tape.gradient(loss, [w1, b1])
# SGD 实现梯度更新 w1 = w1 - lr * w1_grad b = b - lr * b_grad
w1.assign_sub(lr * grads[0]) # 参数w1自更新
b1.assign_sub(lr * grads[1]) # 参数b自更新
2、SGDM
这个优化器顾名思义在SGD的基础上增加了一个momentum环节。也就是增加一个权重系数使算法考虑上一个阶段的梯度大小,增加了算法的时间惯性。其一阶动量和二阶动量分别为
m
t
=
β
?
m
t
?
1
+
(
1
?
β
)
?
g
t
V
t
=
1
m_t= \beta \cdot m_{t-1} + (1- \beta) \cdot g_t \qquad V_t = 1
mt?=β?mt?1?+(1?β)?gt?Vt?=1 所以参数更新计算为:
η
t
=
l
r
?
m
t
V
t
=
l
r
?
(
β
?
m
t
?
1
+
(
1
?
β
)
?
g
t
)
\eta _t= lr\cdot \frac{m_t}{\sqrt{V_t} } =lr\cdot ( \beta \cdot m_{t-1} + (1- \beta) \cdot g_t)
ηt?=lr?Vt??mt??=lr?(β?mt?1?+(1?β)?gt?)
W
t
+
1
=
W
t
?
η
t
=
W
t
?
l
r
?
(
β
?
m
t
?
1
+
(
1
?
β
)
?
g
t
)
W_{t+1} = W_t-\eta _t=W_t- lr\cdot ( \beta \cdot m_{t-1} + (1- \beta) \cdot g_t)
Wt+1?=Wt??ηt?=Wt??lr?(β?mt?1?+(1?β)?gt?)
在SGDM中的mt表示各个时刻下梯度方向的指数滑动平均数。往往mt的参数
?
β
\ \beta
?β会设置一个比较大(接近1)所以上一个时刻的mt会占到较大的比重。使得新计算的梯度更新幅度较小,网络的收敛更加平滑。
loss_all = 0 # 每轮分4个step,loss_all记录四个step生成的4个loss的和
##########################################################################
m_w, m_b = 0, 0 # 初始化一阶和二阶动量,默认初始值为0
beta = 0.9 # 设置一阶动量参数
##########################################################################
now_time = time.time()
for epoch in range(epoch): # 数据集级别的循环,每个epoch循环一次数据集
for step, (x_train, y_train) in enumerate(train_db): # batch级别的循环 ,每个step循环一个batch
with tf.GradientTape() as tape: # with结构记录梯度信息
y = tf.matmul(x_train, w1) + b1 # 神经网络乘加运算
y = tf.nn.softmax(y) # 使输出y符合概率分布(此操作后与独热码同量级,可相减求loss)
y_ = tf.one_hot(y_train, depth=3) # 将标签值转换为独热码格式,方便计算loss和accuracy
loss = tf.reduce_mean(tf.square(y_ - y)) # 采用均方误差损失函数mse = mean(sum(y-out)^2)
loss_all += loss.numpy() # 将每个step计算出的loss累加,为后续求loss平均值提供数据,这样计算的loss更准确
# 计算loss对各个参数的梯度
grads = tape.gradient(loss, [w1, b1]) # 参数w b对loss函数求导
##########################################################################
# sgd-momentun
m_w = beta * m_w + (1 - beta) * grads[0]
m_b = beta * m_b + (1 - beta) * grads[1]
w1.assign_sub(lr * m_w)
b1.assign_sub(lr * m_b)
##########################################################################
# 每个epoch,打印loss信息
print("Epoch {}, loss: {}".format(epoch, loss_all / 4))
train_loss_results.append(loss_all / 4) # 将4个step的loss求平均记录在此变量中
loss_all = 0 # loss_all归零,为记录下一个epoch的loss做准备
上面的代码展示了SGDM的运行过程m_w = beta * m_w + (1 - beta) * grads[0] 计算参数的更新值,然后使用assign_sub函数完成减的动作实现参数更新。
3、AdaGrad
在这个优化器中,进一步的将一阶和二阶动量都进行赋值。相较于SGD而言添加了二阶动量的部分,分别为: m t = g t = ? l o s s ? W t V t = ∑ τ = 1 t g t 2 m_t = g_t= \frac{\partial loss}{\partial W_t} \qquad V_t = \sum_{\tau =1}^{t} g_{t}^{2} mt?=gt?=?Wt??loss?Vt?=τ=1∑t?gt2? η t = l r ? g t ∑ τ = 1 t g t 2 \eta _t = lr \cdot \frac{g_t}{\sqrt{\sum_{\tau =1}^{t} g_{t}^{2} }} ηt?=lr?∑τ=1t?gt2??gt?? 所以每次参数的更新为: W t + 1 = W t ? η t = W t ? l r ? ( g t ∑ τ = 1 t g t 2 ) W_{t+1} = W_t - \eta _t=W_t- lr\cdot ( \frac{g_t}{\sqrt{\sum_{\tau =1}^{t} g_{t}^{2} } } ) Wt+1?=Wt??ηt?=Wt??lr?(∑τ=1t?gt2??gt??)AdaGrad的一阶动量和SGD相同,二阶动量是从开始到当前迭代总的梯度平方和的累计。
##########################################################################
v_w, v_b = 0, 0 # 设置初始的二阶动量为0
##########################################################################
# 训练部分
now_time = time.time()
for epoch in range(epoch): # 数据集级别的循环,每个epoch循环一次数据集
for step, (x_train, y_train) in enumerate(train_db): # batch级别的循环 ,每个step循环一个batch
with tf.GradientTape() as tape: # with结构记录梯度信息
y = tf.matmul(x_train, w1) + b1 # 神经网络乘加运算
y = tf.nn.softmax(y) # 使输出y符合概率分布(此操作后与独热码同量级,可相减求loss)
y_ = tf.one_hot(y_train, depth=3) # 将标签值转换为独热码格式,方便计算loss和accuracy
loss = tf.reduce_mean(tf.square(y_ - y)) # 采用均方误差损失函数mse = mean(sum(y-out)^2)
loss_all += loss.numpy() # 将每个step计算出的loss累加,为后续求loss平均值提供数据,这样计算的loss更准确
# 计算loss对各个参数的梯度
grads = tape.gradient(loss, [w1, b1])
##########################################################################
# adagrad
v_w += tf.square(grads[0]) # 计算参数w二阶动量的和
v_b += tf.square(grads[1]) # 计算参数b二阶动量的和
w1.assign_sub(lr * grads[0] / tf.sqrt(v_w)) # 更新参数,lr * 梯度除以梯度平方和的开根tf.sqrt开根号
b1.assign_sub(lr * grads[1] / tf.sqrt(v_b)) # 更新参数
4、RMSProp
类似于AdaGrad,RMSProp也是在SGD的基础上修改了二阶动量,同时参考到SGDM,在二阶动量中引入上一个时刻的二阶动量,使得二阶动量具有一定的时间惯性。
m
t
=
g
t
=
?
l
o
s
s
?
W
t
V
t
=
β
?
V
t
?
1
+
(
1
?
β
)
?
g
t
2
m_t = g_t=\frac{\partial loss}{\partial W_t} \qquad V_t = \beta \cdot V_{t-1} + (1-\beta) \cdot g_{t}^{2}
mt?=gt?=?Wt??loss?Vt?=β?Vt?1?+(1?β)?gt2? 其中二阶动量的这个加权计算历史值的方法称之为指数滑动平均值。这样的计算方法能够使二阶动量增加的更加平滑。
所以自然的有参数更新为:
η
t
=
l
r
?
m
t
V
t
\eta _t = lr \cdot \frac{m_t}{\sqrt{V_t}}
ηt?=lr?Vt??mt??
W
t
+
1
=
W
t
?
η
t
=
W
t
?
l
r
?
g
t
(
β
?
V
t
?
1
+
(
1
?
β
)
?
g
t
2
)
W_{t+1} = W_t - \eta _t=W_t- lr\cdot \frac{g_t}{(\sqrt{\beta \cdot V_{t-1} + (1-\beta) \cdot g_{t}^{2} } )}
Wt+1?=Wt??ηt?=Wt??lr?(β?Vt?1?+(1?β)?gt2??)gt??
##########################################################################
v_w, v_b = 0, 0 # 初始的二阶动量,默认为0
beta = 0.9 # 权重系数
##########################################################################
# 训练部分
now_time = time.time() ##2##
for epoch in range(epoch): # 数据集级别的循环,每个epoch循环一次数据集
for step, (x_train, y_train) in enumerate(train_db): # batch级别的循环 ,每个step循环一个batch
with tf.GradientTape() as tape: # with结构记录梯度信息
y = tf.matmul(x_train, w1) + b1 # 神经网络乘加运算
y = tf.nn.softmax(y) # 使输出y符合概率分布(此操作后与独热码同量级,可相减求loss)
y_ = tf.one_hot(y_train, depth=3) # 将标签值转换为独热码格式,方便计算loss和accuracy
loss = tf.reduce_mean(tf.square(y_ - y)) # 采用均方误差损失函数mse = mean(sum(y-out)^2)
loss_all += loss.numpy() # 将每个step计算出的loss累加,为后续求loss平均值提供数据,这样计算的loss更准确
# 计算loss对各个参数的梯度
grads = tape.gradient(loss, [w1, b1])
##########################################################################
# rmsprop
v_w = beta * v_w + (1 - beta) * tf.square(grads[0]) # 计算二阶动量
v_b = beta * v_b + (1 - beta) * tf.square(grads[1])
w1.assign_sub(lr * grads[0] / tf.sqrt(v_w)) # 更新参数
b1.assign_sub(lr * grads[1] / tf.sqrt(v_b))
##########################################################################
5、Adam
Adam中的一阶动量和二阶动量分别来自于SGDM和RMSProp。其中一阶动量来自于SGDM二阶动量来自于RMSProp。同时为了避免数据时间惯性导致的误差,还各自引入了偏差矫正。最后的更新值则根据矫正值来进行输出。
对于一阶动量:
m
t
=
β
1
?
m
t
?
1
+
(
1
?
β
1
)
?
g
t
m_t= \beta_1 \cdot m_{t-1} + (1- \beta_1) \cdot g_t
mt?=β1??mt?1?+(1?β1?)?gt? 一阶动量的修正值为:
m
t
^
=
m
t
1
?
β
1
t
\hat{m_t}=\frac{m_t}{1-\beta_1^t}
mt?^?=1?β1t?mt??
对于二阶动量(注意这里的二阶动量的参数)
?
β
\ \beta
?β要重新取值:
V
t
=
β
2
?
V
t
?
1
+
(
1
?
β
2
)
?
g
t
2
V_t = \beta_2 \cdot V_{t-1} + (1-\beta_2) \cdot g_{t}^{2}
Vt?=β2??Vt?1?+(1?β2?)?gt2? 二阶动量的修正值为:
V
t
^
=
V
t
1
?
β
2
t
\hat{V_t}=\frac{V_t}{1-\beta_2^t}
Vt?^?=1?β2t?Vt??
同时最后用于计算的是一二阶动量的修正值,即参数更新为:
η
t
=
l
r
?
m
t
^
V
t
^
=
l
r
?
m
t
1
?
β
1
t
V
t
1
?
β
2
t
\eta _t=lr\cdot\frac{\hat{m_t}}{\sqrt{\hat{V_t}}}=lr\cdot\frac{\frac{m_t}{1-\beta_1^t}}{\sqrt{\frac{V_t}{1-\beta_2^t}}}
ηt?=lr?Vt?^??mt?^??=lr?1?β2t?Vt???1?β1t?mt???
t
=
W
t
?
η
t
=
W
t
?
l
r
?
m
t
1
?
β
1
t
V
t
1
?
β
2
t
_t=W_t-\eta _t=W_t-lr\cdot\frac{\frac{m_t}{1-\beta_1^t}}{\sqrt{\frac{V_t}{1-\beta_2^t}}}
t?=Wt??ηt?=Wt??lr?1?β2t?Vt???1?β1t?mt???
相比另外几个优化器,Adam需要记录的过程变量会更多,主要是一阶二阶动量值,一阶二阶动量校正值:
##########################################################################
m_w, m_b = 0, 0 # 初始化一阶动量
v_w, v_b = 0, 0 # 初始化二阶动量
beta1, beta2 = 0.9, 0.999 # 初始化两个滑膜参数
delta_w, delta_b = 0, 0 # 初始化一阶和二阶动量校正值
global_step = 0 # 记录总的迭代次数
##########################################################################
now_time = time.time()
for epoch in range(epoch): # 数据集级别的循环,每个epoch循环一次数据集
for step, (x_train, y_train) in enumerate(train_db): # batch级别的循环 ,每个step循环一个batch
##########################################################################
global_step += 1
##########################################################################
with tf.GradientTape() as tape: # with结构记录梯度信息
y = tf.matmul(x_train, w1) + b1 # 神经网络乘加运算
y = tf.nn.softmax(y) # 使输出y符合概率分布(此操作后与独热码同量级,可相减求loss)
y_ = tf.one_hot(y_train, depth=3) # 将标签值转换为独热码格式,方便计算loss和accuracy
loss = tf.reduce_mean(tf.square(y_ - y)) # 采用均方误差损失函数mse = mean(sum(y-out)^2)
loss_all += loss.numpy() # 将每个step计算出的loss累加,为后续求loss平均值提供数据,这样计算的loss更准确
# 计算loss对各个参数的梯度
grads = tape.gradient(loss, [w1, b1])
##########################################################################
# adam
m_w = beta1 * m_w + (1 - beta1) * grads[0] # 一阶动量
m_b = beta1 * m_b + (1 - beta1) * grads[1]
v_w = beta2 * v_w + (1 - beta2) * tf.square(grads[0]) # 二阶动量
v_b = beta2 * v_b + (1 - beta2) * tf.square(grads[1])
m_w_correction = m_w / (1 - tf.pow(beta1, int(global_step))) # 一阶动量的校正值
m_b_correction = m_b / (1 - tf.pow(beta1, int(global_step)))
v_w_correction = v_w / (1 - tf.pow(beta2, int(global_step))) #二阶动量的校正值
v_b_correction = v_b / (1 - tf.pow(beta2, int(global_step)))
w1.assign_sub(lr * m_w_correction / tf.sqrt(v_w_correction)) # 更新参数
b1.assign_sub(lr * m_b_correction / tf.sqrt(v_b_correction))
##########################################################################
关于优化器的几个理解
1、如何理解优化器中添加动量时利用上一次数据来计算
答:利用时间惯性加速收敛。首先明确动量法是一种使梯度向量向相关方向加速变化,抑制震荡,最终实现加速收敛的方法。在网络收敛的过程中参数可能是震收敛到最优值,在控制系统中,我们知道要抑制震荡,从反馈的角度来看需要提高系统阻尼,避免局部的突变。那么在网络中,反向传播时计算加入上一次的参数值计算那等效于变相的在局部范围内对这个参数进行了一次求导。此时如果参数连续下降那惯性会加速下降(类似下坡加速)。所以引入惯性可以有效的提高参数在局部范围内自适应变化的能力,达到加快收敛的效果。
在SGD中,一阶动量
m
t
=
β
1
?
m
t
?
1
+
(
1
?
β
1
)
?
g
t
m_t= \beta_1 \cdot m_{t-1} + (1- \beta_1) \cdot g_t
mt?=β1??mt?1?+(1?β1?)?gt? 是各个时刻梯度方向的指数移动平均值,也就是说,t 时刻的下降方向,不仅由当前点的梯度方向决定,而且由此前累积的下降方向决定。通过调整参数的大小,可以调整下降方向是更偏向于历史方向还是当前计算的方向。
当然考虑到参数在快速下降的过程中可能进入局部的最优解(下山的过程中跑太快,只看一小部分,进到了半山的山坳里,以为到山脚了但实际还在半山腰)所以还有人提出更新参数时先计算这一步的梯度g1,但不使用它而是根据历史值再更新一然后在更新后的位置再计算一次梯度g2,看两次梯度的值进行比较。以此来决定新的下降方向。论文-基于SGDM改进的NAG优化。
2、如何理解一阶动量和二阶动量的加入,它们有什么用
答:自使用学习率。回顾在SGD的计算过程中,每一次参数更新时都用到了学习率lr,这是一个预先设置好的参数。在前面的一章中我们讨论了学习率的指数衰减和分段设置。那有没有一种办法可以让学习率自动的根据数据的特点来实现效果呢?答案是肯定的。不过我们要换一种思路——学习率的作用是在反向传播时参数更新的速度,加入不直接改变学习率,而是让这个参数更新的效果能根据数据自适应。所以AdaGrad优化器诞生了,再看一下它的一阶二阶动量:
m
t
=
g
t
=
?
l
o
s
s
?
W
t
V
t
=
∑
τ
=
1
t
g
t
2
m_t = g_t= \frac{\partial loss}{\partial W_t} \qquad V_t = \sum_{\tau =1}^{t} g_{t}^{2}
mt?=gt?=?Wt??loss?Vt?=τ=1∑t?gt2? 变化最大的就是二阶动量是历史梯度值平方的和,由于二阶动量是在分母上,他对数据变化的大小和自身大小成反比趋势。所以达到了这样的效果——假如这个参数经常的更新,那二阶动量求和会累加的很快,使整体更新值变小,导致参数不会应为少数样本发生大幅度变化。反而言之,参数更新的次数和每次的赋值都很小,那么累加求和的值就比较小,这样更新时变化的幅度就比较大。最终实现了学习率不变,但是参数更新却能自适应的调节。
所以不同的二阶动量调整了参数变化的趋势和幅度,但其本质都是为了能自适应的优化参数更新的过程。在上面的AdaGrad优化器中,根据它求和的特性可以知道它更加适合在稀疏离散的数据中,因为数据如果连续,那么二阶动量会单调增加,在一定迭代次数之后会导致学习率直接衰减到0,训练提前结束,这是需要避免的。
由于AdaGrad的学习率衰减策略直接使用连续求和(积分)这样过于激进,为了避免学习率快速衰减到0所以才进一步提出了RMSProp,它的二阶动量使用局部的历史值进行加权计算:
V
t
=
β
?
V
t
?
1
+
(
1
?
β
)
?
g
t
2
V_t = \beta \cdot V_{t-1} + (1-\beta) \cdot g_{t}^{2}
Vt?=β?Vt?1?+(1?β)?gt2? 这样在保留二阶动量累加的基础上又重点关注局部的梯度信息,从而避免了全局求和的缺陷。
3、如何理解Adam的一阶和二阶动量
答:既要又要,既要惯性来加速收敛,又要自适应参数更新幅度。在了解了前面几个优化器之后,很容易发现Adam就是前面优化器的集大成者。他利用了SGDM的一阶动量来增加惯性作用,加速参数的收敛,也利用了RMSProp的二阶动量,在局部范围内利用累加来自适应参数更新的幅度。
4、优化器的选择和小技巧
神经网络算法由于它的特殊性,目前还没有一种算法或优化方式能放之四海而皆准,往往都要根据具体问题和数据特点来单独处理。就比如视觉、RNN网络、稀疏数据分析他们各自都有更好的优化器。
就数据而言,使用RMSprop和Adam在很多情况下效果几乎相同,就理论上来说,首先使用Adam作为优化器是没错的。
当然也可以直接使用没有任何一阶二阶动量的SGD,这样网络收敛的速度可能会比较慢,但是相对可以得到更小的loss。不过SGD由于线性特性也更容易导致算法在局部位置停滞出现局部最优。假如搭建大型复杂的深度神经网络,此时还是更应该使用一些快速收敛的优化器,通过自适应策略来加快网络的训练速度。
构建神经网络时优先关注(算法搭建实用经验)
- 1、首先要了解原始数据的特点,观察其是否存在规律和可以提前消除的噪声数据;
- 2、提供精确有效的标签数据,同时被训练的数据应该充分覆盖研究对象的各个方面;
- 3、先使用小批量的数据来验证网络和算法的可行性,确保训练和预测不报错;
- 4、为了避免数据的局部最优,制作训练数据时可能集中标注了,输入网络前要随机打乱,让网络充分学习到数据中的语义信息,而不是关注局部数据的特点;
- 5、记得在训练训练过程中计时的计算平均损失和验证集正确率,在达到设计要求后适当停止训练。训练的次数并不是越多越好;
- 6、可以在不同的训练阶段使用不同的优化器,比如在训练开始的时候使用Adam来快速收敛,在loss达到一定值时使用SGD和较小的学习率来微调模型。
- 7、在验证数据时可以保存不同阶段的验证情况,这样可以及时发现网络过拟合的出现。
- 8、使用一个合适的学习率衰减策略,可以根据数据的特点,设计自定义的专有学习率衰减策略,让网络的输出朝着期望的方向偏移;
- 9、整个网络中参数的初始赋值很重要,初始值不同收敛的情况甚至最后的结果都会有差异,当算法其他部分稳定时,尽可能尝试多组不同的初始值,选择损失最小的和收敛最快的一组初始值。
博客记录和总结不易,总结前面五篇内容,神经网络基础概念至此已经打通任督二脉。后续会继续通过实际的应用算法加深理解和提高代码构建能力。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- scp传输
- PingCAP 受邀参加 FICC 2023,获 Open100 世纪全球开源贡献奖
- 单元测试计划、用例、报告、评审编制模板
- 【数据结构】链表的分类和双向链表
- 【ArcGIS Pro微课1000例】0057:未安装所需的Microsoft驱动程序
- Midjourney V6有多厉害,看完这27张图你就明白了!
- 普冉32位单片机 PY32C642,M0+内核,1.7 V ~ 5.5 V宽工作电压
- Java内省与反射:灵活操作JavaBean属性的利器
- (一)深度学习入门:感知机模型
- SpringSecurity