【C++】C++算法入门之穷举
前言
本章节主要讲述穷举的相关内容。
学习路线：C++从入门到NOI学习路线
学习大纲：C++全国青少年信息学奥林匹克竞赛（NOI）入门级-大纲
上一站：C++程序结构入门之循环结构四
下一站：
一、概念
每个人都有自己擅长的事，比如有的人擅长体育项目，而有的人更擅长坐下来思考。那计算机擅长什么呢？
没错，计算机更擅长数学计算和数据处理，它能按照设置好的程序对数据进行计算。
举个例子，奥特·海因里希·凯勒（Ott-Heinrich Keller）于90年前提出了凯勒猜想。这个猜想是关于用相同瓷砖覆盖空间的问题，猜测如果用二维正方形瓷砖覆盖二维空间，则至少两个瓷砖必须共享一条边，以此类推，在使用12维“正方形”瓷砖覆盖12维空间时，也至少有两个彼此邻接的瓷砖。
多年来，数学家不断进行证明，发现凯勒猜想在某些维度空间是正确的，但在另一些维度空间是错误的，截至去年10月，仅有七维空间是否正确仍是个谜。
但现在，数学家终于利用计算机解决了这个问题，并发布了证明过程。这是人类独创性结合计算机计算能力解决数学难题的最新示例。
解决这个问题的数学家使用了40台电脑进行计算，30分钟后，机器就给出了一个单词的答案：是的。
能完成这一壮举是因为计算机的运行速度快，善于重复做一件事。
而我们今天要学习的穷举就是利用这一特点，如果我们在数学层面我们短时间内找不到解的公式，那我们可以尝试将所有解的可能都 一 一列出，然后再逐个验证是否符合问题要求，从而找到问题的解。
路人：那怎么使用穷举法呢？
穷举法的步骤如下：
-
确定问题的范围：根据问题的要求，确定需要尝试的数值范围。
-
使用循环进行穷举：使用循环结构（如for循环）遍历范围内的每个数值。
-
将数值带入问题中进行尝试：将当前数值带入问题中，判断是否满足问题的条件。
-
如果满足条件，输出结果或进行其他操作：如果当前数值满足问题的条件，可以输出该数值作为问题的解，或进行其他操作。
-
继续循环直到穷举完所有可能的解。
光说不练假把式，让我们进入到下一环节。
二、单循环样题讲解
问题一：1015 - 鸡兔同笼问题
鸡兔同笼问题：一个笼子里面有鸡若干只，兔若干只。共有头 50 个，共有腿 160 条。求鸡兔各多少只？
1.分析问题
- 已知：头50 个、腿有160个。
- 未知：鸡，兔各多少。
- 关系：鸡 头1腿2，兔 头1腿4。
2.定义变量
根据分析的已知，未知按需要定义变量。
j：鸡
t：兔
//定义鸡、兔的数量。
int j=0,t=0;
3.输入数据
无。
4.数据计算
4.1 确定问题的范围：根据问题的要求，确定需要尝试的数值范围。
t + j = 50，t * 2 + j * 4 = 140
4.2 使用循环进行穷举：使用循环结构（如for循环）遍历范围内的每个数值。
4.3 将数值带入问题中进行尝试：将当前数值带入问题中，判断是否满足问题的条件。
//四、数据计算
while(j*2+(50-j)*4!=160){
j++;
}
4.4 如果满足条件，输出结果或进行其他操作。
t=50-j;
cout<<j<<" "<<t<<endl;
5.输出结果
#include<iostream>
using namespace std;
int main(){
//一、分析问题，已知：头50 个、腿有160个 未知：鸡，兔各多少
//二、数据定义
//定义鸡、兔的数量。
int j=0,t=0;
//三、数据输入
//四、数据计算
while(j*2+(50-j)*4!=160){
j++;
}
t=50-j;
//五、输出结果
cout<<j<<" "<<t<<endl;
return 0;
}
问题二：1351 - 买公园门票
某公园门票价格为：成人票 8元 /张，儿童票 3元 /张；某旅游团来公园游玩，该团内有成人和儿童（成人和儿童都有），共花了 40元买门票。
请你分别计算出成人和儿童可能的人数，按照成人从少到多，儿童从多到少的规律数出结果。
1.分析问题
- 已知：成人票 8 元 / 张，儿童票 3 元 / 张；共花了 40 元买门票。
- 未知：成人和儿童的人数。
- 关系：成人从少到多，儿童从多到少。
2.定义变量
根据分析的已知，未知按需要定义变量。
3.输入数据
无。
4.数据计算
4.1 确定问题的范围：根据问题的要求，确定需要尝试的数值范围。
成人票：最少1张，最多(40-3)/8张，要保证有一张儿童票。
儿童票：最少1张，最多(40-8)/3张，要保证有一张成人票。
4.2 使用循环进行穷举：使用循环结构（如for循环）遍历范围内的每个数值。
i：成人票数量。
for(int i=1;i<=(40-3)/8;i++){
}
4.3 将数值带入问题中进行尝试：将当前数值带入问题中，判断是否满足问题的条件。
j：购买成人票后剩余钱数。
如果j%3==0，说明剩余的钱刚好能买整数个儿童票，符合题意。
//四、数据计算
for(int i=1;i<=(40-3)/8;i++){
int j=40-8*i;
if(j%3==0){
}
}
4.4 如果满足条件，输出结果或进行其他操作。如果当前数值满足问题的条件，可以输出该数值作为问题的解，或进行其他操作。
//四、数据计算
for(int i=1;i<=(40-3)/8;i++){
int j=40-8*i;
if(j%3==0){
//五、输出结果
cout<<i<<" "<<j/3;
}
}
4.5 继续循环直到穷举完所有可能的解。
5.输出结果
#include<iostream>
#include<iomanip>
using namespace std;
int main(){
//一、分析问题
//1. 已知：成人票 8 元 / 张，儿童票 3 元 / 张；共花了 40 元买门票。
//2. 未知：成人和儿童的人数。
//二、数据定义
//三、数据输入
//四、数据计算
for(int i=1;i<=(40-3)/8;i++){
int j=40-8*i;
if(j%3==0){
//五、输出结果
cout<<i<<" "<<j/3;
}
}
return 0;
}
问题三：1016 - 买小猫小狗
某动物饲养中心用 X 元专款购买小狗(每只 A 元)和小猫(每只B 元)两种小动物。
要求专款专用，(至少猫狗各一)，正好用完。
请求出方案的总数。如没有请输出 0 。
1.分析问题
- 已知：小狗 A 元 / 只，小猫 B 元 / 只；共有 X 元。
- 未知：猫狗各一，购买方案总数。
- 关系：A*狗的数量+B * 猫的数量 = X。
2.定义变量
根据分析的已知，未知按需要定义变量。
A：小狗每只价格。
B：小猫每只价格。
X：有多少钱。
count：购买方案的总数。
//二、数据定义
int A,B,X,count=0;
3.输入数据
从键盘读入数据。
//三、数据输入
cin>>X>>A>>B;
4.数据计算
4.1 确定问题的范围：根据问题的要求，确定需要尝试的数值范围。
狗：最少1只，最多(X-B)/A只，要保证有一只猫。
猫：最少1只，最多(X-A)/B张，要保证有一只狗。
4.2 使用循环进行穷举：使用循环结构（如for循环）遍历范围内的每个数值。
a：狗的数量。
//四、数据计算
for(int a=1;a<=(X-B)/A;a++){
}
4.3 将数值带入问题中进行尝试：将当前数值带入问题中，判断是否满足问题的条件。
b：购买狗后剩余钱数。
如果b%B==0，说明剩余的钱刚好能买整数只猫，符合题意。
//四、数据计算
for(int a=1;a<=(X-B)/A;a++){
int b=X-A*a;
if(b%B==0){
}
}
4.4 如果满足条件，输出结果或进行其他操作。如果当前数值满足问题的条件，可以输出该数值作为问题的解，或进行其他操作。
//四、数据计算
for(int a=1;a<=(X-B)/A;a++){
int b=X-A*a;
if(b%B==0){
++count;
}
}
4.5 继续循环直到穷举完所有可能的解。
5.输出结果
#include<iostream>
using namespace std;
int main(){
//一、分析问题
//1. 已知：小狗 A 元 / 只，小猫 B 元 / 只；共有 X 元。
//2. 未知：猫狗各一，购买方案总数。
//二、数据定义
int A,B,X,count=0;
//三、数据输入
cin>>X>>A>>B;
//四、数据计算
for(int a=1;a<=(X-B)/A;a++){
int b=X-A*a;
if(b%B==0){
++count;
}
}
//五、输出结果
cout<<count;
return 0;
}
三、嵌套循环样题讲解
问题一：1022 - 百钱百鸡问题
用 100 元钱买 100 只鸡，公鸡，母鸡，小鸡都要有。
公鸡 5 元 1 只，母鸡 3 元 1 只，小鸡 1 元 3 只。
请问公鸡，母鸡，小鸡各应该买多少只？
1.分析问题
- 已知：共有100元，买100只鸡，公鸡5元1只，母鸡3元1只，小鸡1元3只
- 未知：公鸡g只，母鸡m只，小鸡x只
- 关系：5g+3m+x/3=100，g+m+x=100.
2.定义变量
根据分析的已知，未知按需要定义变量。
//二、数据定义
int money=100,g=1,m=1,x=3;
3.输入数据
无。
4.数据计算
4.1 确定问题的范围：根据问题的要求，确定需要尝试的数值范围。
钱：100。
鸡总数：100。
公鸡：最少1只，最多：(100-3-1)/5只。
母鸡：最少1只，最多：总钱数-已买公鸡数量 * 5 - 最少小鸡，即(money-5*g-1)/3只。
4.2 使用循环进行穷举：使用循环结构（如for循环）遍历范围内的每个数值。
g：公鸡的数量。
while(g<=(100-3-1)/5){
g++;
}
4.3 将数值带入问题中进行尝试：将当前数值带入问题中，判断是否满足问题的条件。
m：母鸡的数量。
母鸡数从多到少。
//四、数据计算
//输出时，按公鸡数从少到多，母鸡数从多到少的顺序输出
while(g<=(100-3-1)/5){
//母鸡最多数量
m=(money-5*g-1)/3;
while(m>1){
x=(money-g*5-m*3)*3;
if(g+m+x==100){
}
m--;
}
g++;
}
4.4 如果满足条件，输出结果或进行其他操作。如果当前数值满足问题的条件，可以输出该数值作为问题的解，或进行其他操作。
//四、数据计算
//输出时，按公鸡数从少到多，母鸡数从多到少的顺序输出
while(g<=(100-3-1)/5){
//母鸡最多数量
m=(money-5*g-1)/3;
while(m>1){
x=(money-g*5-m*3)*3;
if(g+m+x==100){
//五、输出结果
cout<<g<<" "<<m<<" "<<x<<endl;
}
m--;
}
g++;
}
4.5 继续循环直到穷举完所有可能的解。
5.输出结果
#include<iostream>
using namespace std;
int main(){
//一、分析问题
//已知：共有100元，买100只鸡，公鸡5元1只，母鸡3元1只，小鸡1元3只
//未知：公鸡g只，母鸡m只，小鸡x只
//二、数据定义
int money=100,g=1,m=1,x=3;
//三、数据输入
//四、数据计算
//输出时，按公鸡数从少到多，母鸡数从多到少的顺序输出
while(g<=(100-3-1)/5){
//母鸡最多数量
m=(money-5*g-1)/3;
while(m>1){
x=(money-g*5-m*3)*3;
if(g+m+x==100){
//五、输出结果
cout<<g<<" "<<m<<" "<<x<<endl;
}
m--;
}
g++;
}
return 0;
}
问题二：1025 - 兑换硬币
用一张一元票换 1 分、2 分和 5 分的硬币，每种至少一枚， 问有几种换法？
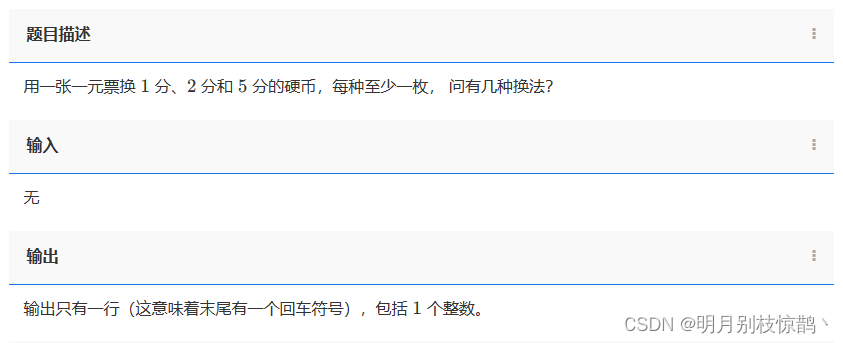
1.分析问题
整体放大100倍，不影响结果。
- 已知：总钱数：100，1元、2元、5元硬币；。
- 未知：1元数量：a；2元数量：b；五元数量：c 。
- 关系：a+2b+5c=100。
2.定义变量
根据分析的已知，未知按需要定义变量。
//二、数据定义
int money=100,a,b,c,count=0;
3.输入数据
无。
4.数据计算
4.1 确定问题的范围：根据问题的要求，确定需要尝试的数值范围。
钱：100。
5元硬币：最少1个，最多：(100-1-2)/5个。
2元硬币：最少1只，最多：总钱数-已换5元硬币数量 * 5 - 1个1元硬币，即(100-1-5*c)/2。
4.2 使用循环进行穷举：使用循环结构（如for循环）遍历范围内的每个数值。
这里我们要优先选择换钱数更大的硬币。
原因1：钱数更大，意味外层循环次更少。
原因2：将1元硬币留在最后，那么不管剩多少钱都是可以换整数个。
4.3 将数值带入问题中进行尝试：将当前数值带入问题中，判断是否满足问题的条件。
//四、数据计算
for(c=1;c<=(100-1-2)/5;c++){
for(b=1;b<=(100-1-5*c)/2;b++){
}
}
4.4 如果满足条件，输出结果或进行其他操作。如果当前数值满足问题的条件，可以输出该数值作为问题的解，或进行其他操作。
//四、数据计算
for(c=1;c<=(100-1-2)/5;c++){
for(b=1;b<=(100-1-5*c)/2;b++){
count++;
}
}
4.5 继续循环直到穷举完所有可能的解。
5.输出结果
#include<iostream>
using namespace std;
int main(){
//一、分析问题
//已知：总钱数：100，1元、2元、5元硬币；
//未知：1元数量：a；2元数量：b；五元数量：c
//二、数据定义
int money=100,a,b,c,count=0;
//三、数据输入
//四、数据计算
for(c=1;c<=(100-1-2)/5;c++){
for(b=1;b<=(100-1-5*c)/2;b++){
count++;
}
}
//五、输出结果
cout<<count;
return 0;
}
问题三：1024 - 购买文具
新学年就要开始了，爸爸把N元钱给了小青，让他购买一批文具，并作了以下要求：只能买圆珠笔、铅笔和铅笔芯，并且每样至少买一支，总数要超过30支，而且钱要全部花完。
当小青去到文具店时，发现圆珠笔8角钱一支、铅笔2角钱一支、铅笔芯1角钱一支。小青怎么买才能符合爸爸的要求呢？请你编个程序帮他算出符合购买要求的所有方案总数。
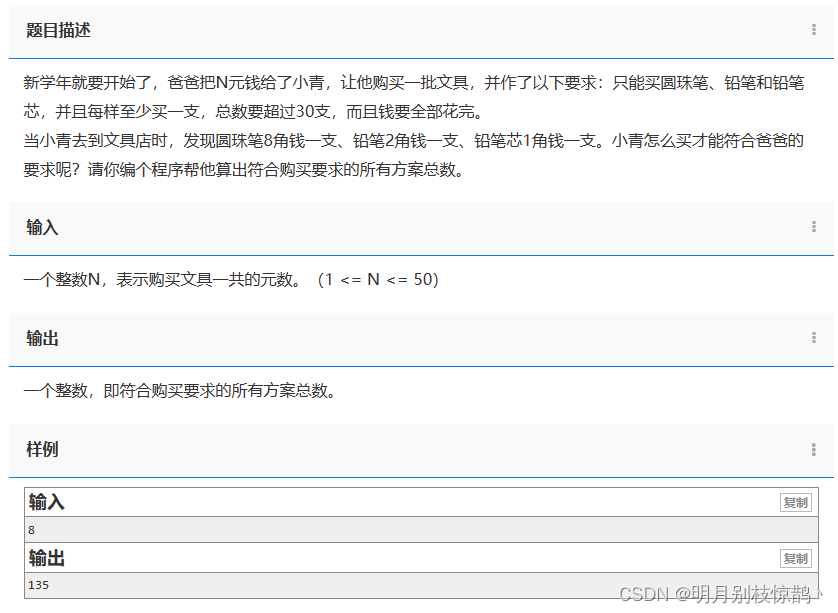
1.分析问题
- 已知：n元钱 圆珠笔8角钱一支、铅笔2角钱一支、铅笔芯1角钱一支。
- 未知：圆珠笔数量a； 铅笔数量b； 铅笔芯数量c。
- 关系：每样一只，总数大于30，钱要花完。
2.定义变量
根据分析的已知，未知按需要定义变量。
count：所有方案总数。
//二、数据定义
int n,a,b,c,count=0;
3.输入数据
从键盘读入钱数。
整体放大10倍，不影响最后的结果。
cin>>n;
n*=10;
4.数据计算
4.1 确定问题的范围：根据问题的要求，确定需要尝试的数值范围。
钱：100。
圆珠笔数量：最少1个，最多：(n-2-1)/8个。
铅笔数量：最少1只，最多：（总钱数-已买圆珠笔数量 * 5 - 1个铅笔芯）/铅笔价格，即(n-a*8-1)/2。
铅笔芯数量：n - a * 8 - b * 2。
4.2 使用循环进行穷举：使用循环结构（如for循环）遍历范围内的每个数值。
4.3 将数值带入问题中进行尝试：将当前数值带入问题中，判断是否满足问题的条件。
如果圆珠笔数量+铅笔数量+铅笔芯数量>30，那么符合题意。
//四、数据计算
for(a=1;a<=(n-2-1)/8;a++){
for(b=1;b<=(n-a*8-1)/2;b++){
c=n-a*8-b*2;
if((a+b+c)>30){
}
}
}
4.4 如果满足条件，输出结果或进行其他操作。如果当前数值满足问题的条件，可以输出该数值作为问题的解，或进行其他操作。
//四、数据计算
for(a=1;a<=(n-2-1)/8;a++){
for(b=1;b<=(n-a*8-1)/2;b++){
c=n-a*8-b*2;
if((a+b+c)>30){
count++;
}
}
}
4.5 继续循环直到穷举完所有可能的解。
5.输出结果
#include<iostream>
using namespace std;
int main(){
//一、分析问题
//已知：n元钱 圆珠笔8角钱一支、铅笔2角钱一支、铅笔芯1角钱一支
//每样一只，总数大于30，钱要花完；
//未知：圆珠笔数量a； 铅笔数量b； 铅笔芯数量c；
//二、数据定义
int n,a,b,c,count=0;
//三、数据输入
cin>>n;
n*=10;
//四、数据计算
for(a=1;a<=(n-2-1)/8;a++){
for(b=1;b<=(n-a*8-1)/2;b++){
c=n-a*8-b*2;
if((a+b+c)>30){
count++;
}
}
}
//五、输出结果
cout<<count;
return 0;
}
四、练习
- 单循环
问题一：1227 - 阿凡提的难题
阿凡提去集市上买餐具，财主正好在卖餐具，所以准备为难一下阿凡提。
财主的餐具有 2 种：大碗和小碗，财主和阿凡提说，你买我的碗，要花光你带的钱，而且，两种碗都要买，买的两种碗的数量都得是偶数。
请你编程帮助阿凡提计算，可以有哪些购买的方案呢？
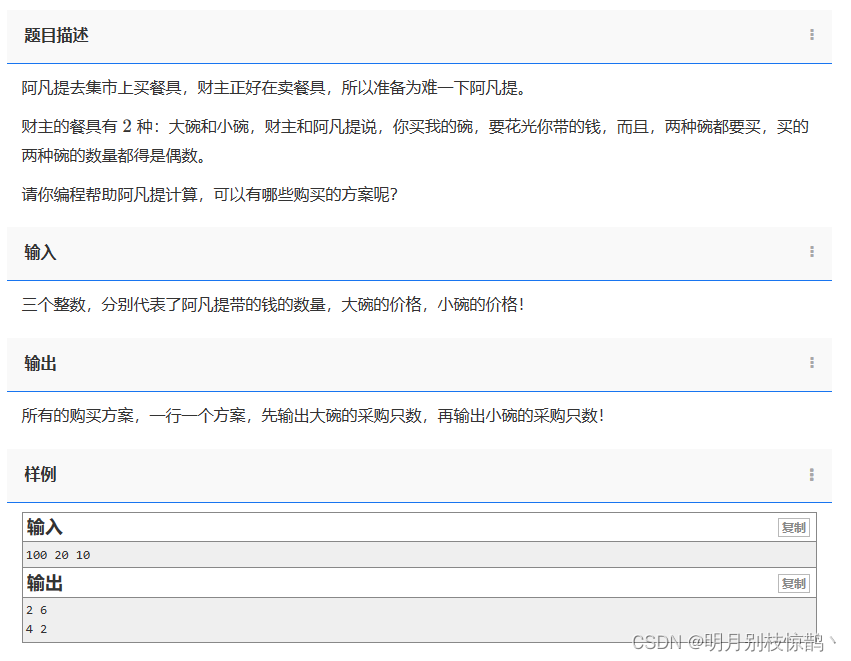
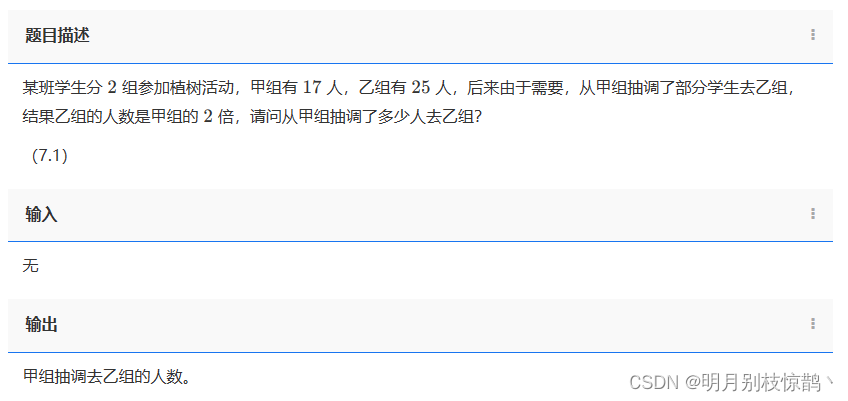
问题二：1349 - 植树的人数
某班学生分 2 组参加植树活动，甲组有 17 人，乙组有 25 人，后来由于需要，从甲组抽调了部分学生去乙组，结果乙组的人数是甲组的 2 倍，请问从甲组抽调了多少人去乙组？
问题三：1396 - 开学大采购？
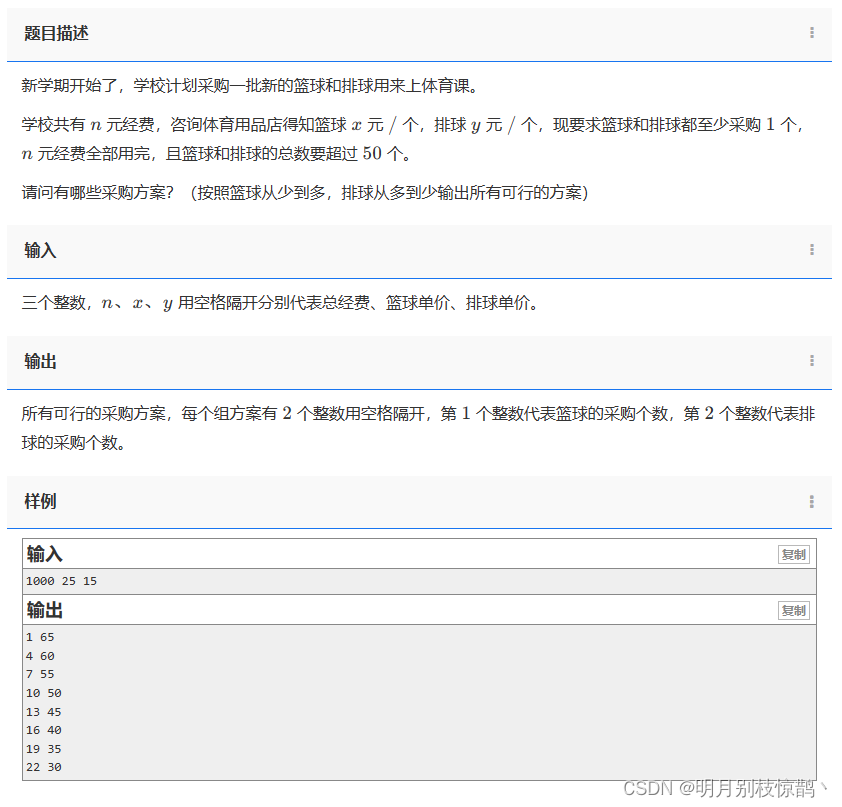
新学期开始了，学校计划采购一批新的篮球和排球用来上体育课。
学校共有 n 元经费，咨询体育用品店得知篮球 x 元 / 个，排球 y 元 / 个，现要求篮球和排球都至少采购 1 个， n 元经费全部用完，且篮球和排球的总数要超过 50 个。
请问有哪些采购方案？（按照篮球从少到多，排球从多到少输出所有可行的方案）
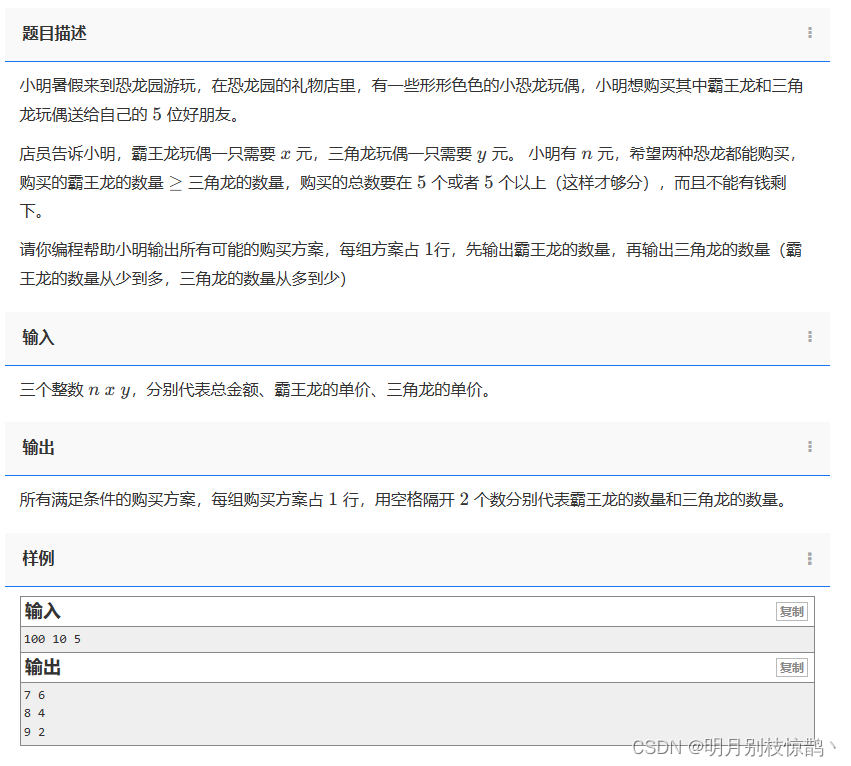
问题四：1394 - 恐龙园买玩具？
小明暑假来到恐龙园游玩，在恐龙园的礼物店里，有一些形形色色的小恐龙玩偶，小明想购买其中霸王龙和三角龙玩偶送给自己的 5位好朋友。
店员告诉小明，霸王龙玩偶一只需要 x 元，三角龙玩偶一只需要 y 元。 小明有 n 元，希望两种恐龙都能购买，购买的霸王龙的数量 ≥ 三角龙的数量，购买的总数要在 5 个或者 5 个以上（这样才够分），而且不能有钱剩下。
请你编程帮助小明输出所有可能的购买方案，每组方案占 1行，先输出霸王龙的数量，再输出三角龙的数量（霸王龙的数量从少到多，三角龙的数量从多到少）
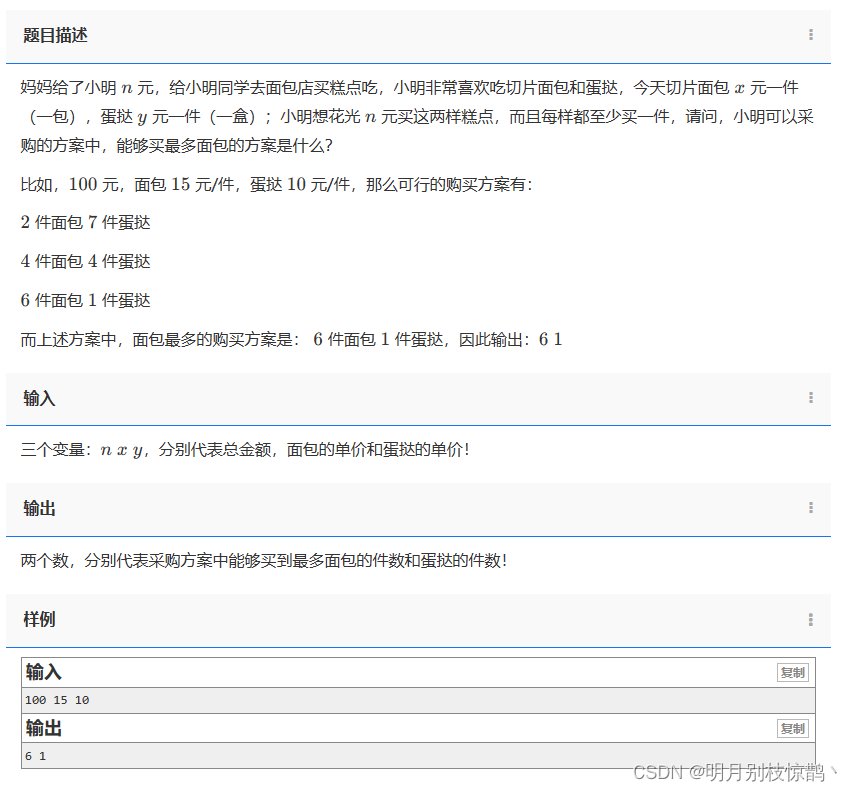
问题五：1220 - 买糕点
妈妈给了小明 n 元，给小明同学去面包店买糕点吃，小明非常喜欢吃切片面包和蛋挞，今天切片面包 x 元一件（一包），蛋挞 y 元一件（一盒）；小明想花光 n 元买这两样糕点，而且每样都至少买一件，请问，小明可以采购的方案中，能够买最多面包的方案是什么？
- 嵌套循环
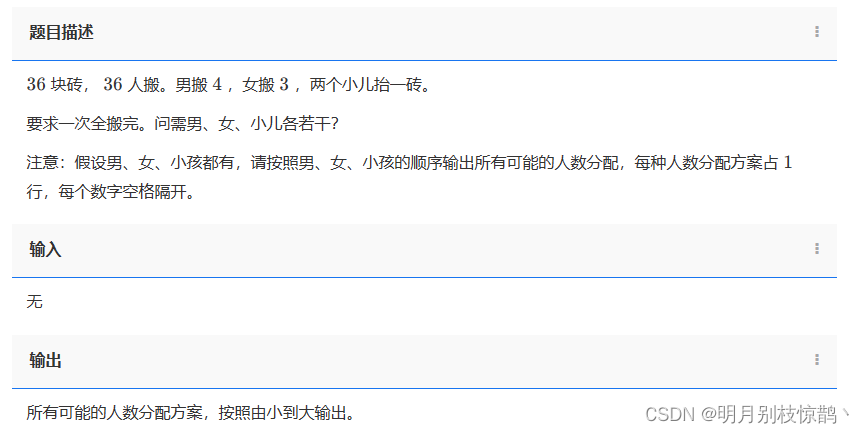
问题一：1249 - 搬砖问题
36 块砖， 36人搬。男搬 4 ，女搬 3 ，两个小儿抬一砖。
要求一次全搬完。问需男、女、小儿各若干？
注意：假设男、女、小孩都有，请按照男、女、小孩的顺序输出所有可能的人数分配，每种人数分配方案占 1 行，每个数字空格隔开。
问题二：1250 - 马克思手稿的问题
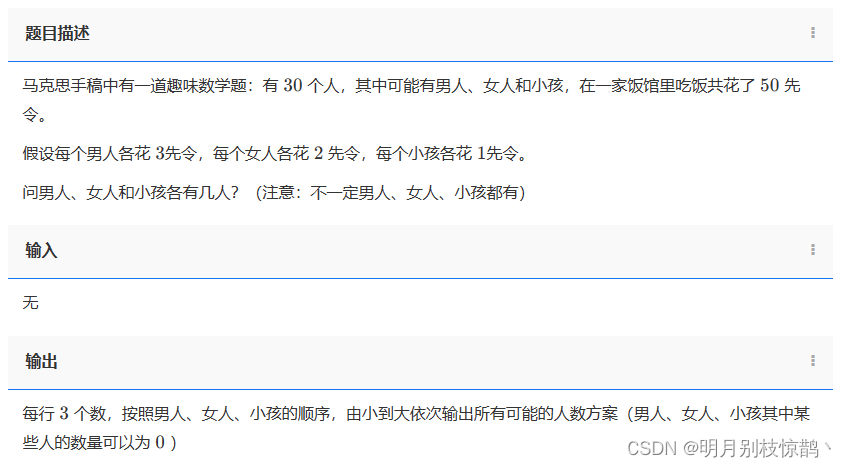
马克思手稿中有一道趣味数学题：有 30 个人，其中可能有男人、女人和小孩，在一家饭馆里吃饭共花了 50 先令。
假设每个男人各花 3先令，每个女人各花 2 先令，每个小孩各花 1先令。
问男人、女人和小孩各有几人？（注意：不一定男人、女人、小孩都有）
问题三：1076 - 桐桐的计算
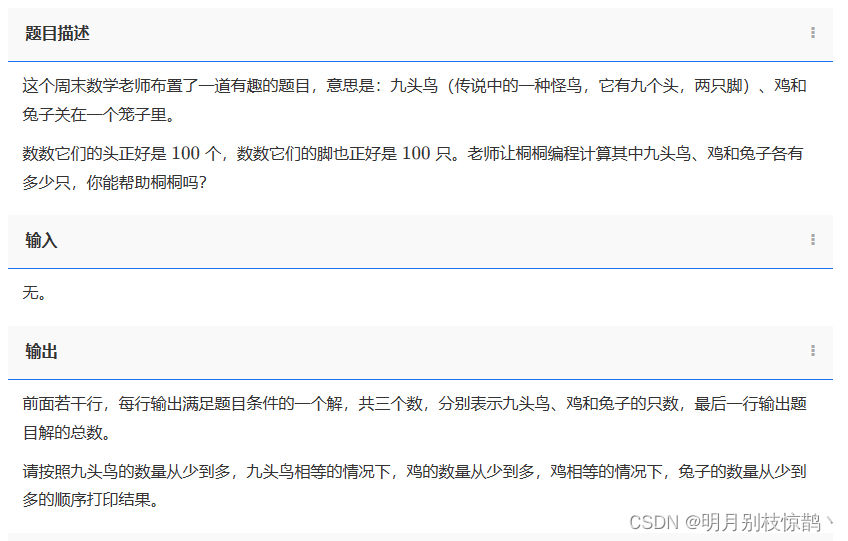
这个周末数学老师布置了一道有趣的题目，意思是：九头鸟（传说中的一种怪鸟，它有九个头，两只脚）、鸡和兔子关在一个笼子里。
数数它们的头正好是 100 个，数数它们的脚也正好是 100 只。老师让桐桐编程计算其中九头鸟、鸡和兔子各有多少只，你能帮助桐桐吗？
问题四：1077 - 桐桐去购物
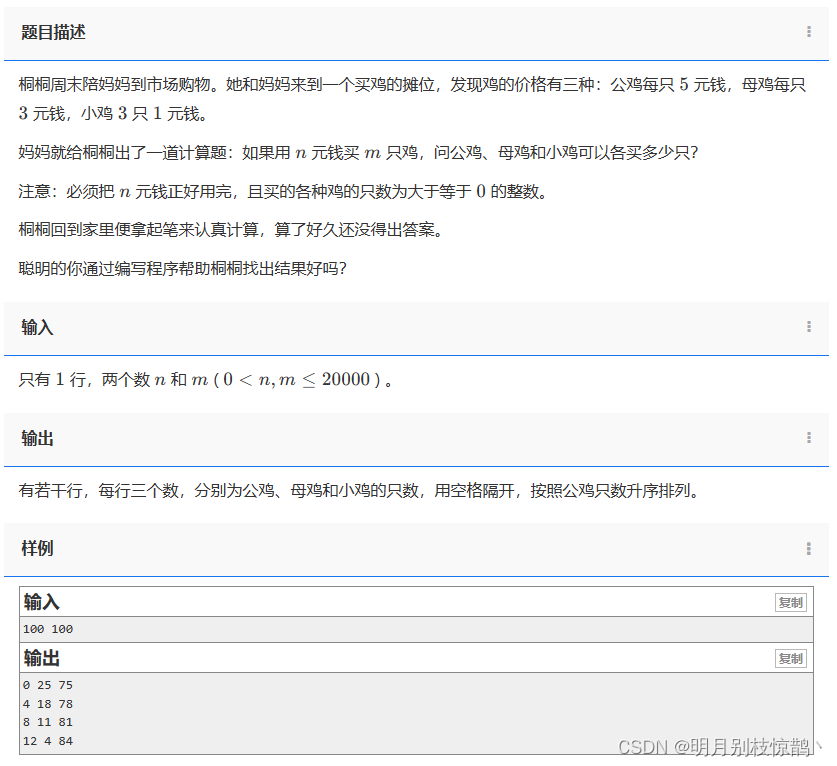
桐桐周末陪妈妈到市场购物。她和妈妈来到一个买鸡的摊位，发现鸡的价格有三种：公鸡每只 5 元钱，母鸡每只 3 元钱，小鸡 3 只 1元钱。
妈妈就给桐桐出了一道计算题：如果用 n 元钱买 m 只鸡，问公鸡、母鸡和小鸡可以各买多少只？
注意：必须把 n 元钱正好用完，且买的各种鸡的只数为大于等于 0 的整数。
桐桐回到家里便拿起笔来认真计算，算了好久还没得出答案。
聪明的你通过编写程序帮助桐桐找出结果好吗？
问题五：1342 - 怎样种树？
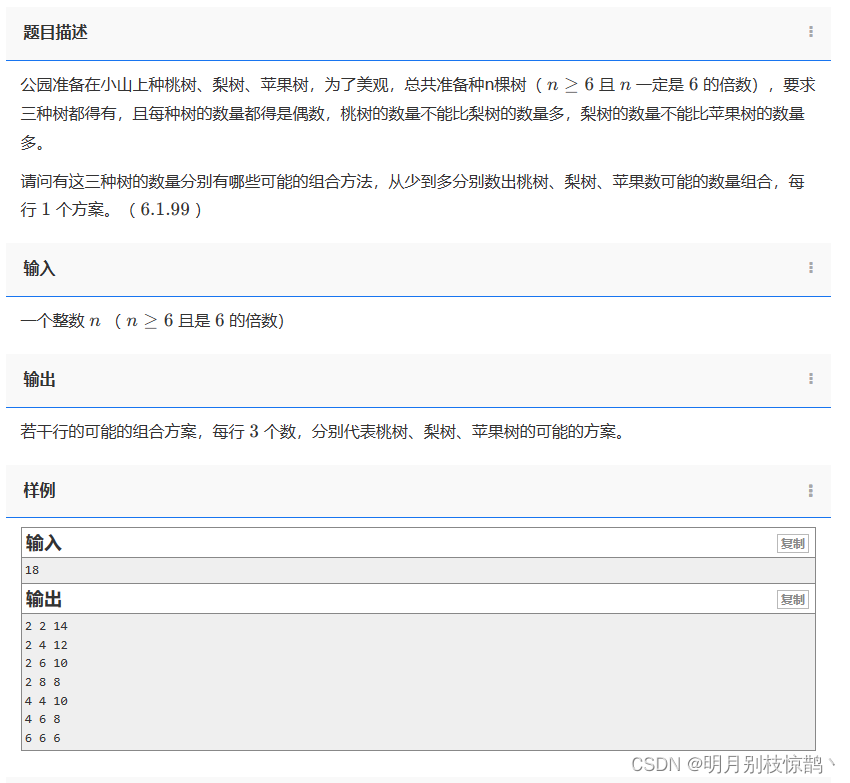
公园准备在小山上种桃树、梨树、苹果树，为了美观，总共准备种n棵树（ n≥6 且 n 一定是 6 的倍数），要求三种树都得有，且每种树的数量都得是偶数，桃树的数量不能比梨树的数量多，梨树的数量不能比苹果树的数量多。
请问有这三种树的数量分别有哪些可能的组合方法，从少到多分别数出桃树、梨树、苹果数可能的数量组合，每行 1 个方案。
五、总结
穷举作为一种古老的算法，它的学习难度并不高。只要按照穷举法5个步骤去思考问题，那么就能找出问题的解。但是在实际应用中，由于穷举法的时间复杂度较高，可能会导致运行时间过长。因此，在使用穷举法时，需要根据问题的规模和复杂度进行合理的范围选择和优化。
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码（1）
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- OAI openair3代码结构整理
- Mac 下载 nvm 后执行nvm -v 命令报错 nvm: command not found
- Ref＜XXX＞的使用
- PHP 平滑重启 kill -SIGUSR2 ＜PID＞
- 注水算法—功率分配
- 【蓝桥杯选拔赛真题81】Scratch旅游相册 第十五届蓝桥杯scratch图形化编程 少儿编程创意编程选拔赛真题解析
- 1.电子基础
- web前端javaScript笔记——（6）数组
- 蚂蚁数科CTO王维首次公开亮相：进一步拓展数据相关技术布局
- 基于JavaWeb+SSM+Vue四六级词汇微信小程序系统的设计和实现