LeetCode-1672/1572/54/73

1.最富有客户的资产总量（1672）

题目描述：

给你一个 m x n 的整数网格 accounts ，其中 accounts[i][j] 是第 i???????????? 位客户在第 j 家银行托管的资产数量。返回最富有客户所拥有的 资产总量 。

客户的 资产总量 就是他们在各家银行托管的资产数量之和。最富有客户就是 资产总量 最大的客户。

思路： 这题很简单遍历矩阵然后累加每一行并且将每一行累加结果放到一个数组中进行记录，然后遍历记录数组返回最大值。

代码：

class Solution {
    public int maximumWealth(int[][] accounts) {
        List<Integer> list=new ArrayList<>();
        for(int i=0;i<accounts.length;i++) {
            int sum=0;
            for(int j=0;j<accounts[i].length;j++) {
                sum+=accounts[i][j];
            }
            list.add(sum);
        }

        int max=0;
        for(int i=0;i<list.size();i++) {
            if(list.get(i)>max) {
                max=list.get(i);
            }
        }

        return max;
    }
}

2.矩阵对角线元素和（1572）

题目描述：

给你一个正方形矩阵 mat，请你返回矩阵对角线元素的和。

请你返回在矩阵主对角线上的元素和副对角线上且不在主对角线上元素的和。

思路： 这题比较简单，遍历矩阵将矩阵两个对角线累加起来，但是如果矩阵的行数是奇数的话，最终返回结果要减掉矩阵中心的元素，因为这个元素在矩阵行数为奇数时在累加时重复了两次。

代码：

class Solution {
    public int diagonalSum(int[][] mat) {
        int sum=0;
        for(int i=0;i<mat.length;i++) {
            sum+=(mat[i][i]+mat[i][mat[0].length-1-i]);
        }

        if(mat.length%2!=0) {
            sum-=mat[mat.length/2][mat.length/2];
        }
        return sum;
    }
}

3.螺旋矩阵（54）

题目描述：

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

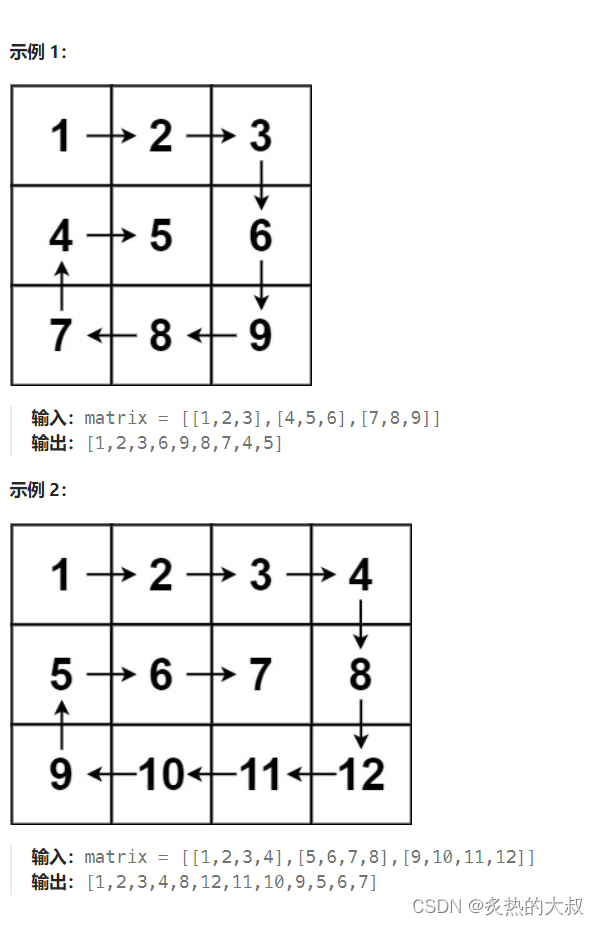
思路： 这题首先明确的是当顺时针遍历矩阵时，到最后一列或者行以及遍历过的元素之前需要变换方向。所以在代码需要建立二维数组来记录哪些元素遍历过了，另外还需要建立一个二维数组来表达变换方向后的移动。具体看代码。

代码：

class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        List<Integer> ret=new ArrayList<Integer>();
        if(matrix==null || matrix.length==0 || matrix[0].length==0) {
            return ret;
        }
        int rows=matrix.length,cols=matrix[0].length;
        boolean[][] visited=new boolean[rows][cols];
        int total=rows*cols;
        int row=0,col=0;
        int[][] direct={{1,0},{0,1},{-1,0},{0,-1}};
        int directIndex=0;
        for(int i=0;i<total;i++) {
            ret.add(matrix[row][col]);
            visited[row][col]=true;
            int nextRow=row+direct[directIndex][1],nextCol=col+direct[directIndex][0];
            if(nextCol<0 || nextCol>=cols || nextRow<0 || nextRow>=rows || visited[nextRow][nextCol]) {
                directIndex=(directIndex+1)%4;
            }
            row=row+direct[directIndex][1];
            col=col+direct[directIndex][0];
        }
        return ret;

    }
}

4.矩阵置零（73）

题目描述：

给定一个 m x n 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。

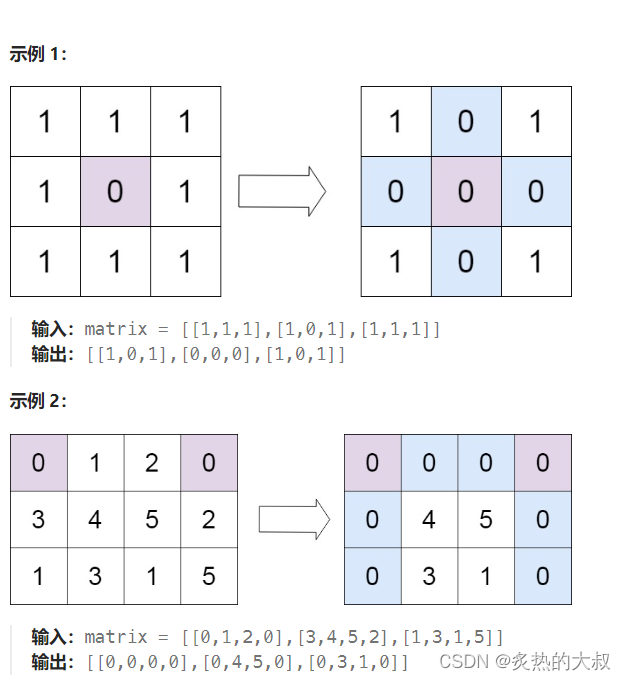
思路： 首先设置两个布尔类型数组，长度分别为矩阵的行数和列数，用于记录。然后遍历矩阵，如果有元素为0，那么将两个布尔型数组在0元素的行号和列号位置处置为true。然后遍历两个布尔型数组，如果有元素true，那么就将该元素对应的矩阵的行数或列数中的元素全置为0。

代码：

class Solution {
    public void setZeroes(int[][] matrix) {
        int rows=matrix.length,cols=matrix[0].length;
        boolean[] rowRecord=new boolean[rows];
        boolean[] colRecord=new boolean[cols];

        for(int i=0;i<rows;i++) {
            for(int j=0;j<cols;j++) {
                if(matrix[i][j]==0) {
                    rowRecord[i]=true;
                    colRecord[j]=true;
                }
            }
        }

        for(int i=0;i<rowRecord.length;i++) {
            if(rowRecord[i]) {
                for(int j=0;j<cols;j++) {
                    matrix[i][j]=0;
                }
            }
        }

        for(int i=0;i<colRecord.length;i++) {
            if(colRecord[i]) {
                for(int j=0;j<rows;j++) {
                    matrix[j][i]=0;
                }
            }
        }
    }
}