【深度强化学习】确定性策略梯度算法 DDPG

前面讲到如 REINFORCE，Actor-Critic，TRPO，PPO 等算法，它们都是随机性策略梯度算法（Stochastic policy），在广泛的任务上表现良好，因为这类方法鼓励了算法探索，给出的策略是各个动作的概率分布。

实际上策略梯度方法分为两类：一类是随机性策略梯度算法，另一类是确定性策略梯度算法。

确定性策略可能更适合需要精确控制的任务，在这些任务中，任何偏离最佳操作的行为都会对结果产生重大影响（如：下棋）。而随机策略可能更适合涉及不确定性或探索的任务，因为它们允许智能体尝试不同的行动并从其结果中学习。

---

DDPG 深度确定性策略梯度 Deep Deterministic Policy Gradient

直觉

DQN 挺好的，但是只能离散动作，不能连续动作，关键原因在于 ${\max }_{a}Q(S,a)$，在无限多的动作下不适用。
解决方法：
$$\underset{a}{\max }Q(s,a)=Q(s,\arg \underset{a}{\max }Q(s,a))\to Q(s,{\mu }_{\theta }(s))$$
核心思想：既然在连续的时候从众多$a$ 里面选一个使得 $Q$ 最大的$a$ 这么难，那我就用一个网络直接近似给出这个$a$，代替这个 max操作，这个网络就叫 ${\mu }_{\theta }$

---

图示

实际上是一种 Actor-Critic 方法

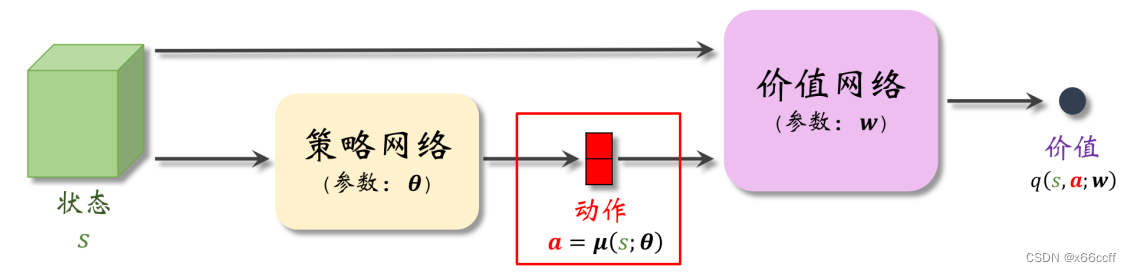
这里策略网络$\mu (s;\theta )$给出的动作 $a$ 是确定的，而不是一个分布。

---

伪代码与解释

• 动作 Clip : 在动作选择的时候，clip，因为动作是连续的，是由神经网络给出的，防止爆nan
• （动作添加噪声 $\mathcal{N}(0,{\sigma }^2)$）：探索 or 稳健
• （动作输入之前批标准化）：平衡连续动作量纲
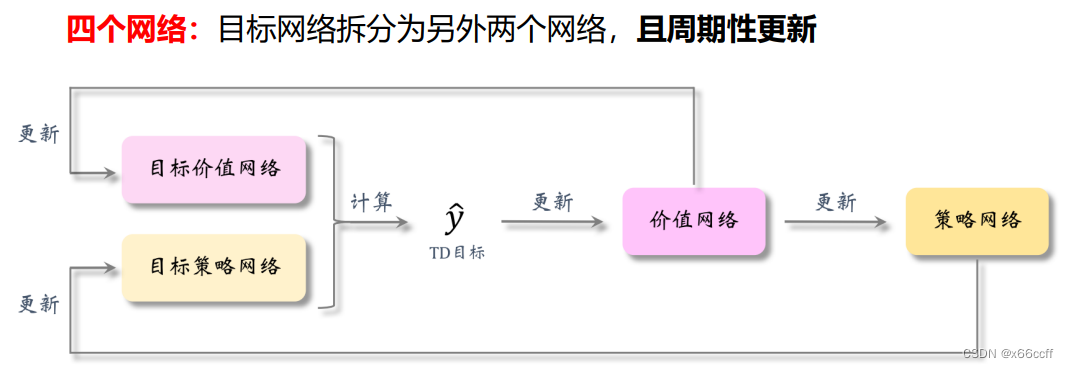
• 每得到一批数据，分别更新 Critic 、 Actor、慢 Critic、慢 Actor:
  • Critic $Q_{?}(?,?)$ 更新：利用 $(r,s^{\prime })$ 计算 TD target，计算的时候都使用 target 参数（${\theta }_{target},{?}_{target}$） ，TD target 和 $Q(s,a)$ 计算 TD loss， 最小化，梯度下降。
  • Actor ${\mu }_{\theta }(?)$ 更新：我们假设 Critic 已经是一个良好的估计，那么就让 $\theta$ 往能够使得 Critic 满意的方向走（选择使得 Critic 满意的连续动作 $a$），最大化，梯度上升。
  • 慢 Critic 和慢 Actor 更新：用移动平均更新即可（思想：类似于 DQN 目标网络，减少自举法带来的偏差）

---

DDPG 加特技

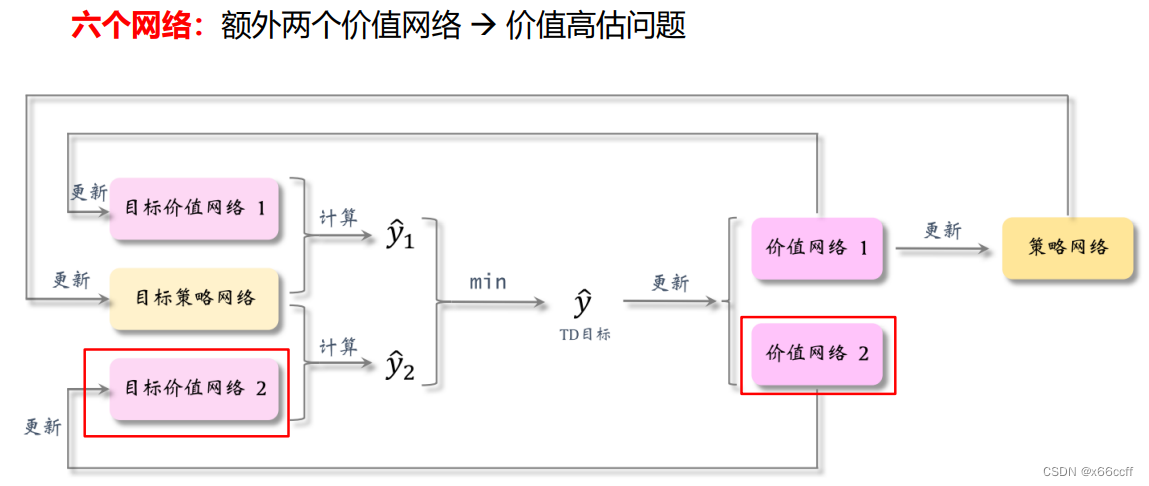
TD3：双延时 DDPG（Twin Delayed Deep Deterministic Policy Gradient）

截断双Q学习：Clipped Double Q-Learning

---

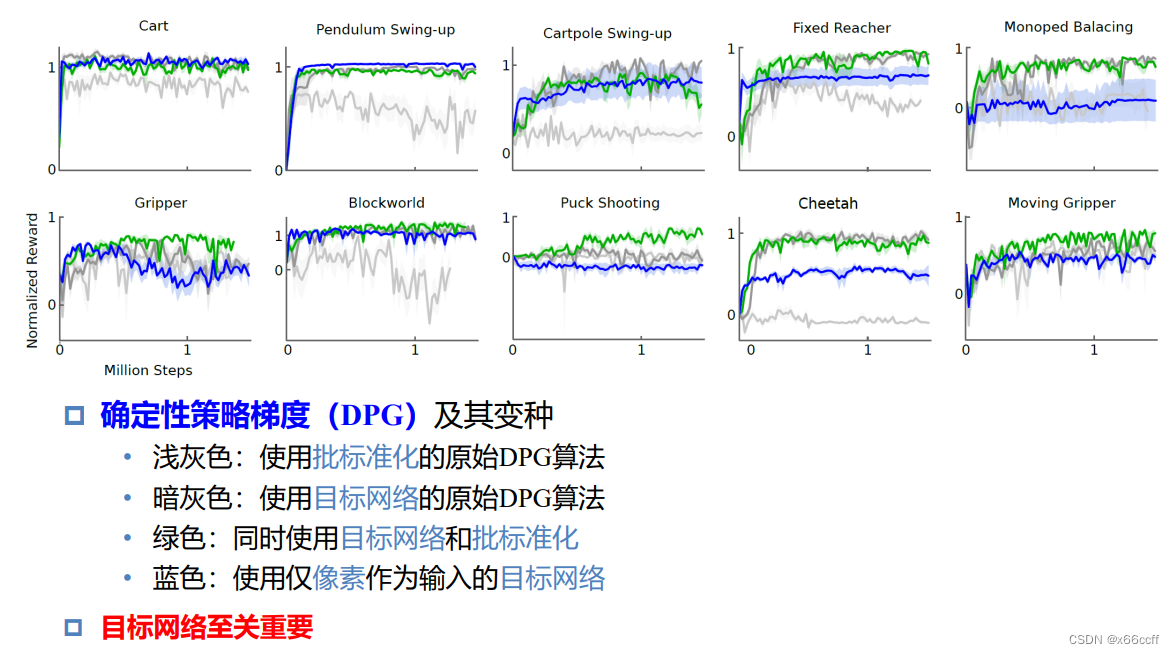
实验效果

---

变化路线