深度剖析数据在内存中的存储

? ? ? ? 1、C语言的各种数据类型?

char //字符数据类型 1个字节
short //短整型 1个字节
int //整型 4个字节
long //长整型 4/8个字节
long long //更长的整型 8个字节
float //单精度浮点数 4个字节
double //双精度浮点数 8个字节

? ? ? ? ?数据类型的大小：决定创建变量时向内存申请了多大的空间。

? ? ? ? 数据的类型：决定内存中这个空间存储了什么类型的数据。

? ? ? ? 注意：C语言没有字符串类型。

? ? ? ? 2、整数在内存中的存储

? ? ? ? ?整数是一个很宽泛的概念，首先我们先说说哪些是整数类型。

? ? ? ? 1、整型家族

? ? ? ? ? ? ?1、char

char:
	signed char //有符号char
	unsigned char	//无符号char

? ? ? ? 由于字符在内存中存储的是它的ASCII码值，故char也属于整形家族。?单对于一个char，它到底是有符号还是无符号是取决于编译器，结果是不确定的。

? ? ? ? 2、short

short:
	signed short //有符号short
	unsigned short //无符号short

? ? ? ? 单独的short默认为有符号short。

? ? ? ? 3、int?

int:
	signed int	//有符号int
	unsigned int //无符号int

? ? ? ? ?单独的int默认为有符号int。

? ? ? ? 4、long

long:
	signed long //有符号long
	unsigned long //无符号long

? ? ? ? 单独的long默认为有符号long。

? ? ? ? 5、long long?

long long:
	signed long long //有符号long long
	unsigned long long //无符号long long

? ? ? ? 单独的long long默认为有符号long long。

? ? ? ? 6、%d和%u

? ? ? ? ?%d打印有符号整型，%u打印无符号整型。

? ? ? ? 2、有符号和无符号的区别（均以int举例）

? ? ? ? 生活中有些数据是没有负数的，故它如果用代码表示，应该用无符号整型。

? ? ? ? 1、signed int

? ? ? ? 对于有符号int，int占四个字节，32个bit位。这时最高位表示符号位。

? ? ? ? 0：代表整数；1：代表负数。

? ? ? ? 2、unsigned int

? ? ? ? 对于无符号int，那么最高位就不代表符号位，而是具有数据意义。

? ? ? ? 3、整型的存储方式

? ? ? ? ?内存中，数据都是以它的二进制补码形式存放的。

? ? ? ? 1、正数的存储

? ? ? ? 正数的二进制补码就是它的二进制原码。（正数的原反补相同）（最高位代表符号位）

? ? ? ? 以13为例：?

? ? ? ? 原码：00000000 00000000 00000000 00001101

? ? ? ? 反码：00000000 00000000 00000000 00001101

? ? ? ? 补码：00000000 00000000 00000000 00001101

? ? ? ? 则13的存储方式就是：00000000 00000000 00000000 00001101

? ? ? ? 2、负数的存储

? ? ? ? 负数的原反补均不相同。（最高位代表符号位）

? ? ? ? 以-13为例：

? ? ? ? 原码：10000000 00000000 00000000 00001101

? ? ? ? 反码：11111111 11111111 11111111 11110010

? ? ? ? 补码：11111111 11111111 11111111 11110011

? ? ? ? 则-13的存储方式就是：11111111 11111111 11111111 11110011。

? ? ? ? 3、整数取出

? ? ? ? 虽然整数是以它的二进制补码方式存储的，但是拿出的时候，均需要转换为二进制原码才能读数。即以二进制原码取出。

? ? ? ? 1、有符号整数取出

signed int a = 4;
// 00000000 00000000 00000000 00000010
//打印结果就是4
printf("%d\n", a);

signed int A = -1;
// 10000000 00000000 00000000 00000001
// 11111111 11111111 11111111 11111110
// 11111111 11111111 11111111 11111111
//取出，补码再变回原码：就还是10000000 00000000 00000000 00000001（最高位代表符号位）
printf("%d\n", A);

? ? ? ? 2、无符号整数取出

? ? ? ? 1、正数

	unsigned int b = 4;
	// 00000000 00000000 00000000 00000010
	//打印结果就是4
	printf("%u\n", b);

? ? ? ? 2、负数

	unsigned int c = -1;
	//首先将-1存储到内存
	//原码： 10000000 00000000 00000000 00000001
	//反码： 11111111 11111111 11111111 11111110
	//补码： 11111111 11111111 11111111 11111111
	//取出无符号b
	//由于我们要的是无符号b，那么此时11111111 11111111 11111111 11111111就是一个正数（最高位不是符号位）
	//不存在符号位，那么此时的补码就是原码，则打印结果十进制就是4294967295
	printf("%u\n", c);//4294967295

? ? ? ? ?3、有符号位和无符号位的表示范围（以8个bit位为例）

????????由此可知：有符号位8进制表示 ???负128（11111111）~127（01111111）

????????无符号位8进制表示 0~255（11111111）

原因：

有符号位：从01111111再往后一位就是10000000，由于是有符号位，且存储方式为二进制补码。所以有符号位的10000000的十进制其实是负128。再往后就是负127，负126.......负1.

补码10000000——>反码01111111——>原码10000000此时是128，由于从它的补码一开始就决定这个数是负的，所以这个数最终为负128

无符号位：高位就不是符号位，所有位就是数字，从00000000-->0,到11111111————>255.

? ? ? ? 3、浮点数在内存中的存储?

? ? ? ? 1、浮点数家族

? ? ? ? 1、float

? ? ? ? ?2、double

? ? ? ? 3、long double

? ? ? ? 2、计算机中的科学计数法表示

????????计算机中的科学计数法（带有E的表示方法）以 E+n 替换部分数字，其中 E（代表指数）表示将前面的数字乘以 10 的 n 次幂。 例如，用 2 位小数的“科学记数”格式表示 12345678901，结果为 1.23E+10，即 1.23 乘以 10 的 10 次幂。 数学术语，a×10的n次幂的形式。

? ? ? ? 3、浮点数表示规则

? ? ? ? 对于任意一个二进制浮点数V，在内存中的存储形式都满足如下公式：

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?V =??(-1)^S * M * 2^E

? ? ? ? 解析：(-1)?^S：代表符号位。S = 0，为正；S = 1，为负。

? ? ? ? ? ? ? ? ? ? ? ? M：表示有效数字，M大于1，小于2。

? ? ? ? ? ? ? ? ? ? ? ? 2^E：代表指数位，2的E次方。

? ? ? ? 举例：1）：V = 5.0（十进制） = 101.0（二进制）= 1.01 * 2^2 = (-1)^0 * 1.01 * 2^2。则S = 0，M = 1.01，E = 2。

? ? ? ? ? ? ? ? ? ? 2）：V = 9.5（十进制） = 1001.1（二进制） = 1.0011 * 2^3 = (-1)^0 * 1.0011 * 2^3。则S = 0，M = 1.0011，E = 3。

? ? ? ? ? ? ? ? ? ? ?3）：V = -2.75（十进制）= -10.11（二进制） = - 1.011 * 2^1 = (-1)^1 * 1.011 * 2^1。则S = 1，M = 1.011，E = 1。

? ? ? ? 4、浮点数存储规则

? ? ? ? 1、单精度浮点数存储

? ? ? ? 对于32位的单精度浮点数存储，规定：最高的1位为符号位S；接着8位是指数E，剩下23位是有效数字M。

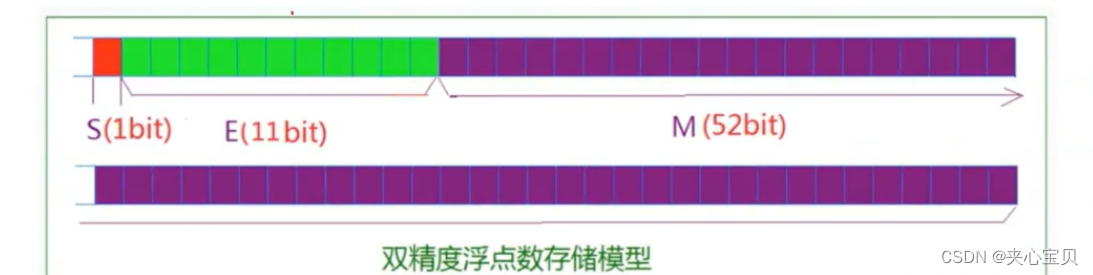
? ? ? ? 2、双精度浮点数存储?

? ? ? ? 对于64位的双精度浮点数存储，规定：?最高的1位为符号位S；接着11位是指数E，剩下52位是有效数字M。

?????????3、特殊规定对于E和M：

? ? ? ?1、?M：?

????????由于1 <= M < 2，所以M可以表示为1.xxxxxxxx，其中xxxxxxx表示小数部分。那么特别规定，M在计算机内存中保存时，省去1，只保留xxxxxxxx部分。（例如1.01，保存时只保留01，等到取出的时候再加上1和小数点即可）这样做的目的是为了节省一个有效数位。?

? ? ? ?2、E：

????????对于E就比较复杂。首先，E是一个无符号整型，那么如果是8位，E属于0-255；11位，E属于0-2047。但是从科学计数法中我们可以知道，E是可以出现负数的。所以我们规定：在将E存入内存之前，E的真实值需要加上一个中间数，最后得到的值才存入内存。对于这个中间数，8位下为127，11位下为1023。（比如2^10,此时E = 10，对于32位浮点数，存入内存的E = 10 + 127 + 137，即是10001001）

? ? ? ? ?3、举例：

? ? ? ? 如上的V = 9.5 =(-1)^0 * 1.0011 * 2^3。则S = 0，M = 1.0011，E = 3（11二进制）。那么存入内存时：S = 0，M存为?= 0011，E = 3+127 = 130 = 1000 0010?。则9.5在内存中地址表示为：

0 10000010 0011000 0000 0000 0000 0000（对于M，右边剩下的位置全部0补全）转成16进制的内存表示就为：0x41 18 00 00

? ? ? ? 5、浮点数取出?

? ? ? ? 对于浮点数取出时，M加上那个1和小数点。然而对于E的结果有三种不同的情况。

? ? ? ? 1、E不全为0或不全为1

? ? ? ? 这就是正常情况，取出时将E减去127或者1023即可

? ? ? ? 2、E全为0

? ? ? ? 对于E全为0，可以理解为，初始的E加上127或者1023后，E接近0。那么就说明，初始的E是一个很大的负数，即说明最初的V值是一个很小的数。那么最后取出的时候，我们就将M表示为0.xxxxxxxx，不将1加上。这样是为了表示无限接近于0的很小的数字。E就取-126或者-1022即可。

? ? ? ? 3、E全为1

? ? ? ? 对于E全为1，可以理解为，初始的E加上127或者1023后，E已经变为255或者2047，那么说明初始的E也已经是127或者1023了，那么就可以说明原来的V值是一个很大的数。即可以表示V是一个正（负）无穷的数。

? ? ? ? 4、总结

? ? ? ? 数据的存储并不是一件简单的事，想要真正了解其中，还得走很长一段路啊，任重而道远啊。