【算法挨揍日记】day46——377. 组合总和 Ⅳ\、96. 不同的二叉搜索树

发布时间：2024年01月04日

?377. 组合总和 Ⅳ

377.?组合总和 Ⅳ

题目描述：

给你一个由?不同?整数组成的数组?nums?，和一个目标整数?target?。请你从?nums?中找出并返回总和为?target?的元素组合的个数。

题目数据保证答案符合 32 位整数范围。

解题思路：

算法思路：
?定要注意，我们的背包问题本质上求的是「组合」数问题，?这?道题求的是「排列数」问题。
因此我们不能被这道题给迷惑，还是?常规的 dp 思想来解决这道题。
1. 状态表?：
这道题的状态表?就是根据「拆分出相同?问题」的?式，抽象出来?个状态表?：
当我们在求 target 这个数?共有?种排列?式的时候，对于最后?个位置，如果我们拿出数组
中的?个数 x ，接下来就是去找 target - x ?共有多少种排列?式。
因此我们可以抽象出来?个状态表?：
dp[i] 表?：总和为 i 的时候，?共有多少种排列?案。
2. 状态转移?程：
对于 dp[i] ，我们根据「最后?个位置」划分，我们可以选择数组中的任意?个数
nums[j] ，其中 0 <= j <= n - 1 。
当 nums[j] <= target 的时候，此时的排列数等于我们先找到 target - nums[j] 的?
案数，然后在每?个?案后?加上?个数字 nums[j] 即可。
因为有很多个 j 符合情况，因此我们的状态转移?程为： dp[i] += dp[target -
nums[j] ，其中 0 <= j <= n - 1 。
3. 初始化：
当和为 0 的时候，我们可以什么都不选，「空集」?种?案，因此 dp[0] = 1 。
4. 填表顺序：
根据「状态转移?程」易得「从左往右」。
5. 返回值：
根据「状态表?」，我们要返回的是 dp[target] 的值。

解题代码：

class Solution {
public:
    int combinationSum4(vector<int>& nums, int target) {
            int n=nums.size();
            vector<double>dp(target+1);
            dp[0]=1;
            for(int i=1;i<=target;i++)
            {
                for(int j=0;j<n;j++)
                    if(i>=nums[j])dp[i]+=dp[i-nums[j]];
            }
            return dp[target];
    }
};

96. 不同的二叉搜索树

96.?不同的二叉搜索树

题目描述：

给你一个整数?n?，求恰由?n?个节点组成且节点值从?1?到?n?互不相同的?二叉搜索树?有多少种？返回满足题意的二叉搜索树的种数。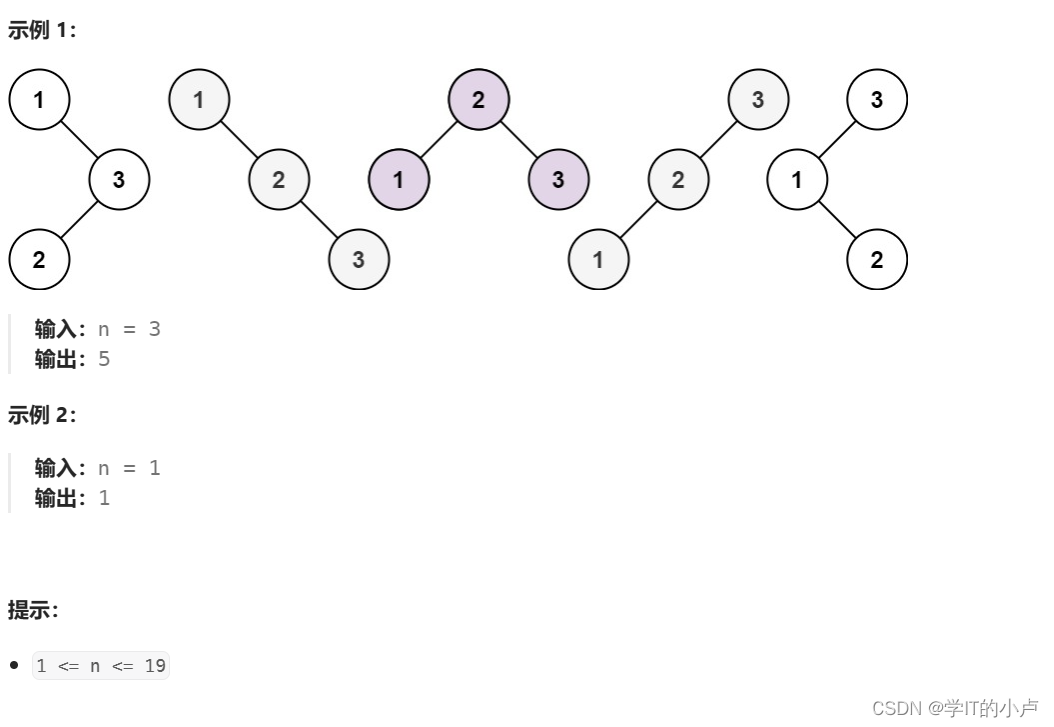

解题思路：

算法思路：
这道题属于「卡特兰数」的?个应?，同样能解决的问题还有「合法的进出栈序列」、「括号匹配
的括号序列」、「电影购票」等等。如果感兴趣的同学可以「百度」搜索卡特兰数，会有很多详细
的介绍。
1. 状态表?：
这道题的状态表?就是根据「拆分出相同?问题」的?式，抽象出来?个状态表?：
当我们在求个数为 n 的 BST 的个数的时候，当确定?个根节点之后，左右?树的结点「个数」
也确定了。此时左右?树就会变成相同的?问题，因此我们可以这样定义状态表?：
dp[i] 表?：当结点的数量为 i 个的时候，?共有多少颗 BST 。
难的是如何推导状态转移?程，因为它跟我们之前常?的状态转移?程不是很像。
2. 状态转移?程：
对于 dp[i] ，此时我们已经有 i 个结点了，为了?便叙述，我们将这 i 个结点排好序，并且编
上 1, 2, 3, 4, 5.....i 的编号。
那么，对于所有不同的 BST ，我们可以按照下?的划分规则，分成不同的 i 类：「按照不同的
头结点来分类」。分类结果就是：
i. 头结点为 1 号结点的所有 BST
ii. 头结点为 2 号结点的所有 BST
iii. ......
如果我们能求出「每?类中的 BST 的数量」，将所有类的 BST 数量累加在?起，就是最后结
果。
接下来选择「头结点为 j 号」的结点，来分析这 i 类 BST 的通?求法。
如果选择「 j 号结点来作为头结点」，根据 BST 的定义：
i. j 号结点的「左?树」的结点编号应该在 [1, j - 1] 之间，?共有 j - 1 个结点。
那么 j 号结点作为头结点的话，它的「左?树的种类」就有 dp[j - 1] 种（回顾?下
我们 dp 数组的定义哈）；
ii. j 号结点的「右?树」的结点编号应该在 [j + 1, i] 之间，?共有 i - j 个结点。那
么 j 号结点作为头结点的话，它的「右?树的种类」就有 dp[i - j] 种；
根据「排列组合」的原理可得： j 号结点作为头结点的 BST 的种类?共有 dp[j - 1] *
dp[i - j] 种！
因此，我们只要把「不同头结点的 BST 数量」累加在?起，就能得到 dp[i] 的值： dp[i]
+= dp[j - 1] * dp[i - j] ( 1 <= j <= i) 。「注意?的是 += ，并且 j 从 1 变
化到 i 」。
3. 初始化：
我们注意到，每?个状态转移??的 j - 1 和 i - j 都是?于 i 的，并且可能会?到前?
个的状态（当 i = 1 ， j = 1 的时候，要?到 dp[0] 的数据）。因此要先把第?个元素初始
化。
当 i = 0 的时候，表??颗空树，「空树也是?颗?叉搜索树」，因此 dp[0] = 1 。
4. 填表顺序：
根据「状态转移?程」，易得「从左往右」。
5. 返回值：
根据「状态表?」，我们要返回的是 dp[n] 的值。

?解题代码：

class Solution {
public:
    int numTrees(int n) {
        vector<int> dp(n + 1,0); // dp[i] 表?：当结点的数量为 i 个的时候，?共有多少颗 BST
        dp[0] = 1;                       // 空树也是?颗?叉搜索树
        for (int i = 1; i <= n; i++)     // 枚举结点的总数
            for (int j = 1; j <= i; j++) // 选择每?个根节点
                dp[i] += dp[j - 1] * dp[i - j]; // ?叉树总量累加在?起
        return dp[n];
    }
};

文章来源:https://blog.csdn.net/m0_69061857/article/details/135346695
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章