算法第九天-二叉搜索树的范围和
二叉搜索树的范围和
题目要求
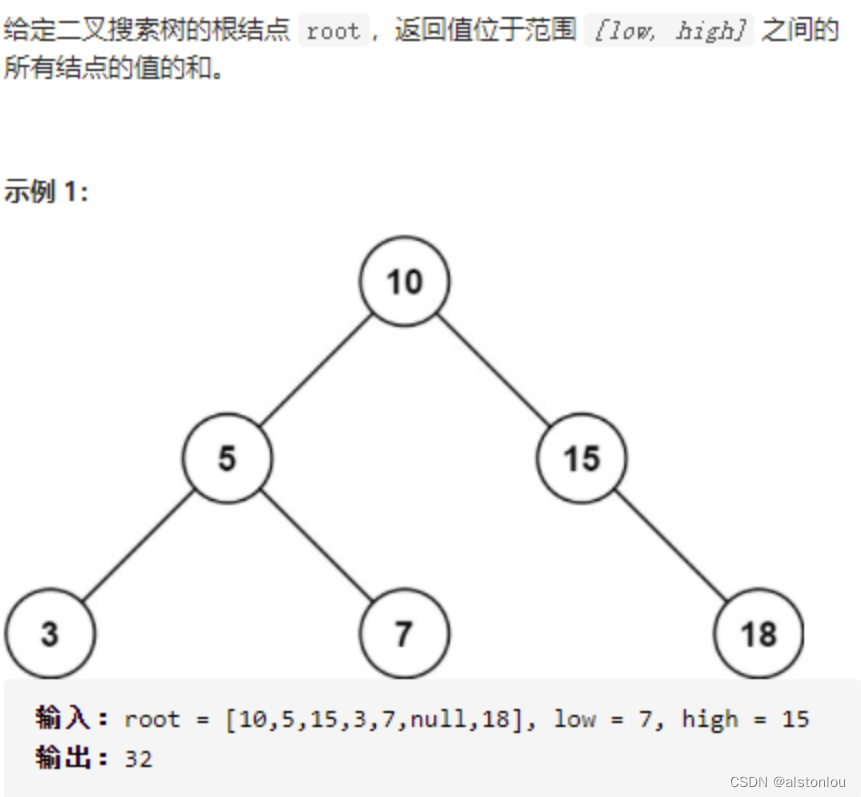
解题思路
来自[负雪明烛]
本题重点:二叉搜索树,最重要的性质:二叉搜索树的中序遍历是有序的。
本题没有直接使用有序的性质,而是使用了二叉树的定义:每个节点的所有左子树都小于当前节点;每个节点的所有右子树都大于当前节点。
直接递归
加入给出的是一棵普通的二叉树,是如何求所有在[low,high]之间的节点值只和呢?我们可以使用递归对所有节点遍历一次,前序、中序、后续均可,累加所有节点值在[low,high]之间的节点值。
要写出递归,最基本的就是要清晰地理解并记住递归函数的定义
我们为什么要用递归?是因为我们发现可以把大问题拆分成小问题,小问题恰好符合现有函数的定义,所以就用来这个函数。由于这个函数是本身,所以我们将其称为递归,在递归函数的时候,把它当作普通函数用,当作黑盒子用,只要知道了函数的含义、输入和输出就行了。不要去想这个函数内部做了什么事情。
剪枝
上面的方法中,是直接使用普通二叉树来进行计算的,其实题目给出的是二叉搜索树,所以可以根据其性质进行剪枝。
- 二叉搜索树的左子树一定比root小,因此如果root.val<= low,那么不用继续搜索左子树;
- 二叉搜索树的右子树一定比root大,因此如果root.val>=high,那么不用继续搜索右子树。
经过剪枝的递归,能减少搜索的空间。因此在树特别庞大的时候,速度更快。
代码
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def rangeSumBST(self, root: TreeNode, low: int, high: int) -> int:
return self.dfs(root,high,low)
def dfs(self,Tree,h,l):
if not Tree: return 0
elif Tree.val < l:
return self.dfs(Tree.right,h,l)
elif Tree.val > h:
return self.dfs(Tree.left,h,l)
else:
return Tree.val + self.dfs(Tree.right,h,l) + self.dfs(Tree.left,h,l)
复杂度分析
时间复杂度:
O
(
N
)
O(N)
O(N)
空间复杂度:
O
(
N
)
O(N)
O(N)
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 阿富汗塔利班兴起时的比赛代码3475:练85.3 删数问题(Noip1994)
- C++string类的介绍及常用函数用法总结
- linux docker-compose安装失败解决
- 使用Qt连接scrcpy-server控制手机
- 【深度总结】MyBatis 批量插入的多种方式及对比
- JDBC-数据库连接池(druid)
- 02-编程猜谜游戏
- 基于朴素Bayes分类的强化学习及在游戏中的应用
- redis 三主六从高可用dockerswarm高级版(不固定ip)
- ftp连接报错:227 entering passive mode