论文阅读《Domain Generalized Stereo Matching via Hierarchical Visual Transformation》
概述
?? 立体匹配模型是近年来的研究热点。但是,现有的方法过分依赖特定数据集上的简单特征,导致在新的数据集上泛化能力不强。现有的立体匹配方法在训练过程中容易学习合成数据集中的表面特征(捷径特征 shortcut features)。这些特征主要有两种伪影(artifacts):一是局部颜色统计特征的一致性,二是对局部色度特征的过度依赖。这些特征不能有效地适应不同域之间的迁移。之前的研究主要关注于(1)利用目标域的有标签数据对模型进行微调。(2)同时使用有标签的合成数据集和无标签的真实数据集来训练域自适应立体匹配模型。这些方法在目标数据集的样本可获得时可以取得较好的效果,但在分布外泛化时性能不佳。为了解决这些问题,文中提出了分层视觉变换(Hierarchical Visual Transformation, HVT)网络,其核心思想是通过改变合成数据集训练数据的分布,使得模型不依赖于源域样本的伪影特征(颜色统计、色度特征)来建立匹配关系,而是引导模型学习域不变的特征(语义特征、结构特征)来估计视差图。
??为了解决立体匹配的域泛化问题,本文提出了一种分层的视觉变换网络(Hierarchical Visual Transformation,HVT),它能从合成数据集中学习一种不受捷径特征干扰的特征表示,从而减少域偏移对模型性能的影响。该网络主要包括两个部分:(1)在全局、局部和像素三个层次上,对训练样本进行视觉变换,使其适应新的数据域。(2)通过最大化源域和目标域之间的视觉特征差异,以及最小化跨域特征之间的一致性,来得到域不变的特征。这样可以防止模型利用合成数据集中的伪影信息作为捷径特征,从而有效地学习到鲁棒的特征表示。我们将HVT模块嵌入到主流的立体匹配模型中,在多个数据集上的实验结果表明,HVT可以提高模型从合成数据集到真实数据集之间的域泛化能力。
模型架构
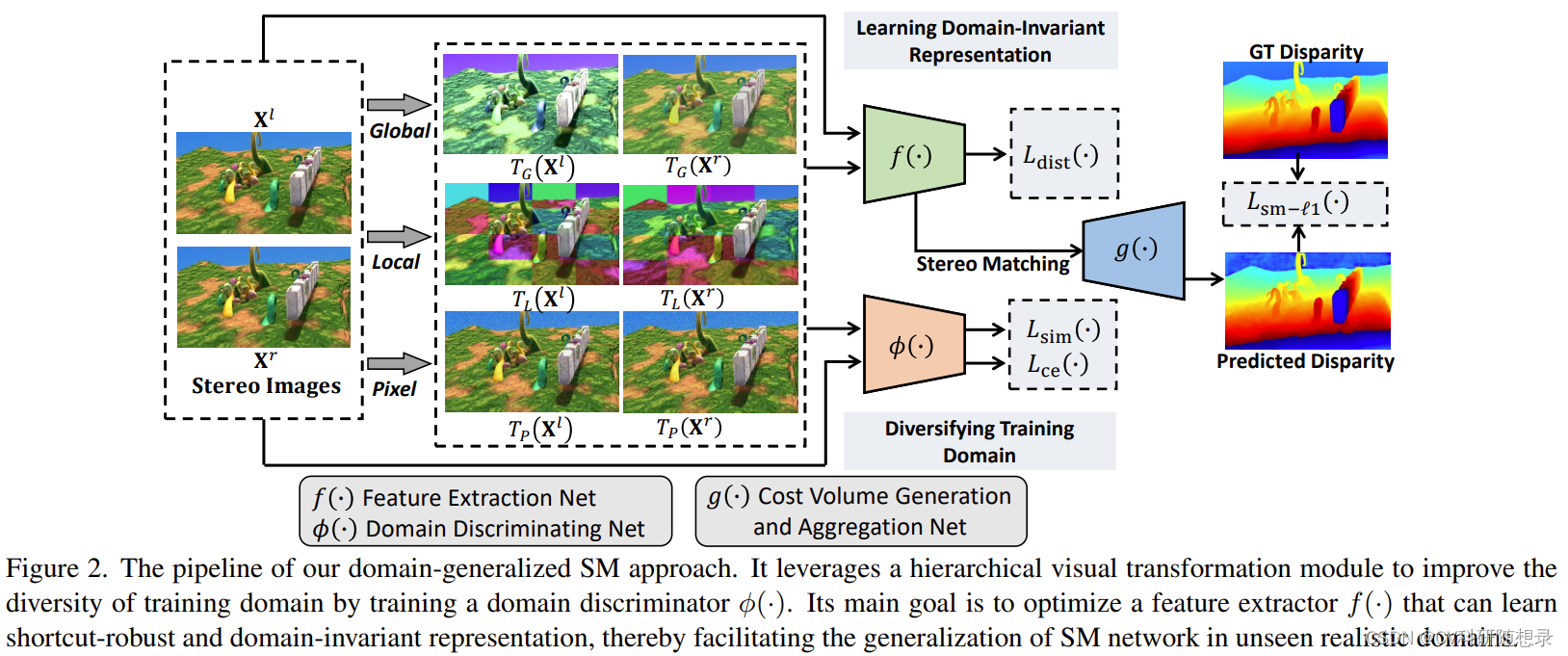
?? 给定合成训练数据集
D
s
\mathcal{D}_{s}
Ds? ,训练集中的图像对为
{
X
i
l
,
X
i
r
}
i
=
1
∣
D
s
∣
\{\mathbf{X}_i^l,\mathbf{X}_i^r\}_{i=1}^{|\mathcal{D}_s|}
{Xil?,Xir?}i=1∣Ds?∣?, 且其对应的视差图为
{
Y
i
g
t
}
i
=
1
∣
D
s
∣
\{\mathbf{Y}_i^{gt}\}_{i=1}^{|\mathcal{D}_s|}
{Yigt?}i=1∣Ds?∣?。模型的目标为训练一个跨域立体匹配模型来预测未知域
D
r
\mathcal{D}_{r}
Dr? 的图像对:
Y
^
=
F
Θ
(
X
l
,
X
r
)
=
s
(
g
(
f
(
X
l
)
,
f
(
X
r
)
)
)
,
(1)
\hat{\mathbf{Y}}=F_\Theta(\mathbf{X}^l,\mathbf{X}^r)=s\big(g\big(f(\mathbf{X}^l),f(\mathbf{X}^r)\big)\big),\tag{1}
Y^=FΘ?(Xl,Xr)=s(g(f(Xl),f(Xr))),(1)
其中
Θ
\Theta
Θ 为模型的人全部参数,
f
(
?
)
f(\cdot)
f(?) 表示特征提取模块,
g
(
?
)
g(\cdot)
g(?) 表示代价体构建、聚合,
s
(
?
)
s(\cdot)
s(?) 表示soft-argmin操作,经典的立体匹配模型通过平滑
L
1
L1
L1 损失
L
sm-
?
1
(
F
Θ
(
X
l
,
X
r
)
,
Y
g
t
)
L_{\text{sm-}\ell_1}\left(F_\Theta(\mathbf{X}^l,\mathbf{X}^r),\mathbf{Y}^{gt}\right)
Lsm-?1??(FΘ?(Xl,Xr),Ygt) 来优化模型。
Hierarchical Visual Transformation 分层视觉转换(核心为图像增强)
??分层视觉转换模块旨在学习到域不变的匹配特征,如语义特征与结构特征,为此,在不同层次学习一系列视觉转换 T = { T 1 , ? ? , T M } \mathcal{T}=\{T_1,\cdots,T_M\} T={T1?,?,TM?} 来将输入图像映射到域不变的特征空间 ( T ( X l ) , T ( X r ) ) \left(T(\mathbf{X}^l),T(\mathbf{X}^r)\right) (T(Xl),T(Xr)),视觉转换应该具有以下的要求:
- T ( ? ) T(\cdot) T(?) 应使得转换前后的图像具有较大的视觉差异,以扩充训练域的多样性。
- T ( ? ) T(\cdot) T(?) 不应改变原始图像对应的视差图。当输入左右图像时候,仍然应优化 L sm- ? 1 ( F Θ ( T ( X l ) , T ( X r ) ) , Y g t ) L_{\text{sm-}\ell_1}(F_\Theta(T(\mathbf{X}^l),T(\mathbf{X}^r)),\mathbf{Y}^{gt}) Lsm-?1??(FΘ?(T(Xl),T(Xr)),Ygt) 目标。
- f ( T ( X ) ) f(T(\mathbf{X})) f(T(X)) 与 f ( X ) f(\mathbf{X}) f(X) 应该具有一致性,以获得域不变的特征。
为此,作者在全局、局部、像素三个层级设计了视觉不变转换。
全局转换
??全局视觉转换
T
G
(
?
)
T_{G}(\cdot)
TG?(?) 旨在以一个全局的视角改变立体图像的视觉特征分布,包括亮度、对比度、饱和度和色调
{
T
G
B
,
T
G
C
,
T
G
S
,
T
G
H
}
\{T_G^B,T_G^C,T_G^S,T_G^H\}
{TGB?,TGC?,TGS?,TGH?}. 其中,
{
T
G
B
,
T
G
C
,
T
G
S
ˉ
}
\{T_{G}^{B},T_{G}^{C},T_{G}^{\bar{S}}\}
{TGB?,TGC?,TGSˉ?} 可以表示为:
T
G
I
(
X
)
=
α
G
I
X
+
(
1
?
α
G
I
)
o
I
(
X
)
,
(2)
T_G^I(\mathbf{X})=\alpha_G^I\mathbf{X}+(1-\alpha_G^I)o^I(\mathbf{X}),\tag{2}
TGI?(X)=αGI?X+(1?αGI?)oI(X),(2)
其中
I
∈
{
B
,
G
,
S
}
I\in\{B,G,S\}
I∈{B,G,S} ,
α
G
I
\alpha_{G}^I
αGI? 为随机在
[
τ
min
?
I
,
τ
max
?
I
]
[\tau_{\min}^I,\tau_{\max}^I]
[τminI?,τmaxI?] 选择的对比度参数:
{
τ
m
i
n
I
=
1
?
(
μ
σ
(
?
l
I
)
+
β
)
τ
m
a
x
I
=
1
+
(
μ
σ
(
?
h
I
)
+
β
)
,
(3)
\left.\left\{\begin{array}{c}\tau_\mathrm{min}^I=1-\left(\mu\sigma(\varrho_l^I)+\beta\right)\\\tau_\mathrm{max}^I=1+\left(\mu\sigma(\varrho_h^I)+\beta\right)\end{array}\right.\right.,\tag{3}
{τminI?=1?(μσ(?lI?)+β)τmaxI?=1+(μσ(?hI?)+β)?,(3)
其中
σ
(
?
)
\sigma(\cdot)
σ(?) 代表 Sigmoid函数。
?
l
I
∈
R
1
,
?
h
I
∈
R
1
\varrho_l^I\in\mathbb{R}^1, \varrho_h^I\in\mathbb{R}^1
?lI?∈R1,?hI?∈R1 为两个可学习的参数。
μ
,
β
\mu,\beta
μ,β 为两个正的超参数。公式2中的
o
I
(
?
)
o^{I}(\cdot)
oI(?) 的定义为 (1)对于亮度转换:
o
B
(
X
)
=
X
?
O
o^B(\mathbf{X})=\mathbf{X}\cdot\mathbf{O}
oB(X)=X?O ,其中
O
\mathbf{O}
O 为全0的矩阵。(2)对于对比度变换:
o
C
(
X
)
=
Avg
?
(
Gray
?
(
X
)
)
o^C(\mathbf{X})=\operatorname{Avg}(\operatorname{Gray}(\mathbf{X}))
oC(X)=Avg(Gray(X)) ,其中
?Gray
(
?
)
\text{ Gray}(\cdot)
?Gray(?) 表示将图像转换为灰度图像,
Avg
?
(
?
)
\operatorname{Avg}(\cdot)
Avg(?) 表示整张图像的灰度平均值。(3)对于饱和度转换,
o
S
(
X
)
=
G
r
a
y
(
X
)
o^S(\mathbf{X})=\mathrm{Gray}(\mathbf{X})
oS(X)=Gray(X)。
??对于色调转换,有:
T
G
H
(
X
)
=
R
g
b
(
[
h
+
α
G
H
,
s
,
v
]
)
,
(4)
T_G^H(\mathbf{X})=\mathrm{Rgb}([\mathbf{h}+\alpha_G^H,\mathbf{s},\mathbf{v}]),\tag{4}
TGH?(X)=Rgb([h+αGH?,s,v]),(4)
其中
[
h
,
s
,
v
]
=
H
s
v
(
X
)
\left[\mathbf{h},\mathbf{s},\mathbf{v}\right]=\mathrm{Hsv}(\mathbf{X})
[h,s,v]=Hsv(X) 表示将图像转换到HSV空间的表示。
Rgb
?
(
?
)
\operatorname{Rgb}(\cdot)
Rgb(?)表示从HSV空间转换到RGB空间。
α
G
H
∈
R
1
\alpha_{G}^{H}\in\mathbb{R}^{1}
αGH?∈R1 表示从
[
τ
m
i
n
H
ˉ
,
τ
m
a
x
H
]
[\tau_{\mathrm{min}}^{\bar{H}},\tau_{\mathrm{max}}^{H}]
[τminHˉ?,τmaxH?] 随机采样的参数,且
τ
m
i
n
H
=
?
μ
σ
(
?
l
H
)
?
β
,
τ
m
a
x
H
=
μ
σ
(
?
h
H
)
+
β
\tau_{\mathrm{min}}^{H}=-\mu\sigma(\varrho_{l}^{H})-\beta , \tau_{\mathrm{max}}^{H}=\mu\sigma(\varrho_{h}^{H})+\beta
τminH?=?μσ(?lH?)?β,τmaxH?=μσ(?hH?)+β。此外,
{
T
G
B
,
T
G
C
,
T
G
S
,
T
G
H
}
\{T_G^B,T_G^C,T_G^S,T_G^H\}
{TGB?,TGC?,TGS?,TGH?} 的顺序是随机的。
局部级变换
??局部视觉转换
T
L
(
?
)
T_{L}(\cdot)
TL?(?)旨在在局部范围改变训练图像的分布。将图像分为
N
′
×
N
′
N^{\prime}\times N^{\prime}
N′×N′ 个不重叠的块
{
x
1
p
,
?
?
,
x
N
′
×
N
′
p
}
\{\mathbf{x}_1^p,\cdots,\mathbf{x}_{N^{\prime}\times N^{\prime}}^p\}
{x1p?,?,xN′×N′p?},将每个块视为独立的图像,使用随机参数的局部转换
T
L
p
(
?
)
T_{L}^{p}(\cdot)
TLp?(?) 分别进行转换后拼接回原图大小:
T
L
(
X
)
=
M
e
r
g
e
(
[
T
L
p
(
x
1
p
)
,
?
?
,
T
L
p
(
x
N
′
×
N
′
p
)
]
)
,
(5)
T_L(\mathbf{X})=\mathsf{Merge}\left([T_L^p(\mathbf{x}_1^p),\cdots,T_L^p(\mathbf{x}_{N^{\prime}\times N^{\prime}}^p)]\right),\tag{5}
TL?(X)=Merge([TLp?(x1p?),?,TLp?(xN′×N′p?)]),(5)
其中局部变换模块可以利用现有的风格迁移网络来实现,或者基于傅里叶的方法,为了与全局变换模块相配合,局部变换模块采用了与全局模块一样的变换函数。
像素级变换
??像素级的视觉变换旨在像素层级进行随机变换:
T
P
(
X
)
=
X
+
(
μ
σ
(
W
)
+
β
)
P
(6)
T_P(\mathbf{X})=\mathbf{X}+\begin{pmatrix}\mu\sigma(\mathbf{W})+\beta\end{pmatrix}\mathbf{P}\tag{6}
TP?(X)=X+(μσ(W)+β?)P(6)
其中
P
∈
R
H
×
W
×
3
\mathbf{P}\in\mathbb{R}^{H\times W\times3}
P∈RH×W×3 为随机生成均值为0,方差为1的的高斯矩阵。
W
∈
R
H
×
W
×
3
\mathbf{W}\in\mathbb{R}^{H\times W\times3}
W∈RH×W×3 为可学习的矩阵。
损失函数
跨域视觉差异最大化:该方法的目的是使数据在变换后的视觉特征分布与变换前的分布有明显的差异,同时保持变换前后的匹配特征表示的一致性,从而学习到不受域影响的特征。这样,立体匹配网络就可以忽略数据中的伪影,更有效地利用学习到的鲁棒特征表示来估计视差:
max
?
L
d
i
s
c
(
X
)
=
1
3
∑
J
d
(
T
J
(
X
)
,
X
)
(7)
\max L_{\mathrm{disc}}(\mathbf{X})=\frac13\sum_{J}d(T_J(\mathbf{X}),\mathbf{X})\tag{7}
maxLdisc?(X)=31?J∑?d(TJ?(X),X)(7)
其中
J
∈
{
G
,
L
,
P
}
J\in\{G,L,P\}
J∈{G,L,P} ,
d
(
?
)
d(\cdot)
d(?) 是域差异度量,作者引入一个神经网络模块
?
(
?
)
\phi(\cdot)
?(?) 来提取域差异特征,则式7可以表示为:
min
?
L
sin
?
(
X
)
=
1
3
∑
J
C
o
s
(
?
(
T
J
(
X
)
)
,
?
(
X
)
)
,
(8)
\min L_{\sin}(\mathbf{X})=\frac13\sum_J\mathrm{Cos}\left(\phi(T_J(\mathbf{X})),\phi(\mathbf{X})\right),\tag{8}
minLsin?(X)=31?J∑?Cos(?(TJ?(X)),?(X)),(8)
为了进一步提升域差异,使用交叉熵损失来优化模型:
min
?
L
c
e
(
X
)
=
C
E
(
{
?
(
T
J
(
X
)
)
,
?
(
X
)
}
,
Y
d
)
,
(9)
\min L_{\mathfrak{ce}}(\mathbf{X})=\mathrm{CE}\left(\left\{\phi(T_J(\mathbf{X})),\phi(\mathbf{X})\right\},\mathcal{Y}_d\right),\tag{9}
minLce?(X)=CE({?(TJ?(X)),?(X)},Yd?),(9)
其中
Y
d
\mathcal{Y}_d
Yd? 表示四个变换域的域标签。
跨域特征一致性最大化:为了增强模型的泛化能力,模型需要获取域不变的匹配特征,这要求变换 T ( ? ) T(\cdot) T(?) 不改变原图的语义与结构特征。因此,最小化以下的损失:
min ? L d i s t ( X ) = 1 3 ∑ J ∥ f ( T J ( X ) ) ? f ( X ) ∥ 2 , (10) \min L_{\mathrm{dist}}(\mathbf{X})=\frac13\sum_J\left\|f\left(T_J(\mathbf{X})\right)-f\left(\mathbf{X}\right)\right\|_2,\tag{10} minLdist?(X)=31?J∑?∥f(TJ?(X))?f(X)∥2?,(10)
总的损失函数:
min
?
L
=
L
s
m
?
?
1
(
Y
^
,
Y
g
t
)
+
1
2
(
λ
1
L
d
i
s
t
(
X
)
+
λ
2
L
s
i
m
(
X
)
+
λ
3
L
c
e
(
X
)
)
,
(11)
\begin{aligned}\min\mathcal{L}=&L_{\mathrm{sm-}\ell_1}(\hat{\mathbf{Y}},\mathbf{Y}^{gt})+\frac12\left(\lambda_1L_{\mathrm{dist}}(\mathbf{X})+\lambda_2L_{\mathrm{sim}}(\mathbf{X})+\lambda_3L_{\mathrm{ce}}(\mathbf{X})\right),\end{aligned}\tag{11}
minL=?Lsm??1??(Y^,Ygt)+21?(λ1?Ldist?(X)+λ2?Lsim?(X)+λ3?Lce?(X)),?(11)
其中 L sm- ? 1 L_{\text{sm-}\ell_1} Lsm-?1?? 同时在 { X l , X r } \{\mathbf{X}^l,\mathbf{X}^r\} {Xl,Xr} 与 { T J ( X l ) , T J ( X r ) } \{T_J(\mathbf{X}^l),T_J(\mathbf{X}^r)\} {TJ?(Xl),TJ?(Xr)} 作为模型输入时计算。
实验结果





本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!