算法训练第六十天|84.柱状图中最大的矩形
发布时间:2024年01月06日
84.柱状图中最大的矩形:
题目链接
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
示例 :
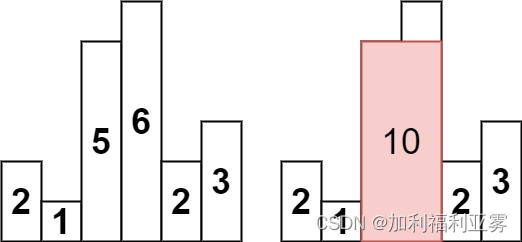
输入:heights = [2,1,5,6,2,3]
输出:10
解释:最大的矩形为图中红色区域,面积为 10
解答:
class Solution {
int largestRectangleArea(int[] heights) {
Stack<Integer> st = new Stack<Integer>();
// 数组扩容,在头和尾各加入一个元素
int [] newHeights = new int[heights.length + 2];
newHeights[0] = 0;
newHeights[newHeights.length - 1] = 0;
for (int index = 0; index < heights.length; index++){
newHeights[index + 1] = heights[index];
}
heights = newHeights;
st.push(0);
int result = 0;
// 第一个元素已经入栈,从下标1开始
for (int i = 1; i < heights.length; i++) {
// 注意heights[i] 是和heights[st.top()] 比较 ,st.top()是下标
if (heights[i] > heights[st.peek()]) {
st.push(i);
} else if (heights[i] == heights[st.peek()]) {
st.pop(); // 这个可以加,可以不加,效果一样,思路不同
st.push(i);
} else {
while (heights[i] < heights[st.peek()]) { // 注意是while
int mid = st.peek();
st.pop();
int left = st.peek();
int right = i;
int w = right - left - 1;
int h = heights[mid];
result = Math.max(result, w * h);
}
st.push(i);
}
}
return result;
}
}
算法总结:
本题整体思路实际上和上一题接雨水的思路是一样的,唯一不同的是接雨水我们希望求比当前柱子更低的柱子,而本题我们要求更高的柱子,所以在单调栈判断入栈上的处理上不同,即heights[i] > heights[st.peek()]时,当前元素入栈。
文章来源:https://blog.csdn.net/lenwu222/article/details/135432964
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 增量预训练,在所属领域数据上继续预训练,主要问题是灾难性遗忘
- maven搭建编程环境
- C语言常见关键字
- 从零学Java - Lambda表达式
- imx8mm平台flash镜像组成(imx-atf\ firmware-imx-8m\imx-boot\u-boot-imx\optee-os )
- 新能源电池展-2024年北京新能源电池技术展在顺义馆召开!
- k8s集群master节点的删除和重新加入
- Pytorch的默认初始化分布 nn.Embedding.weight初始化分布
- CodeWave智能开发平台--03--目标:应用创建--08联系人管理
- win10电脑提示“KBDSG.DLL文件缺失”,软件游戏无法启动运行,快速修复方法