C语言 B树的分析与实现
本文主要说明了B树的概念、应用以及如何用C语言实现B树。
概述
有使用过数据库的朋友都知道,数据库需要存储大量的数据,并且查询数据的性能也需要一定的保证。那么数据库的底层数据结构是如何实现的呢,就是我们要讨论的B树和B+树,数据库使用的是B+树,B+树以B树为基础,本文主要也是讨论B树,并实现B树。
磁盘结构
为什么这里需要提及磁盘呢,这是因为数据库需要存储大量的数据,内存肯定无法存储这些数据,需要借助磁盘来完成数据的存储,查询数据库实际上也是对磁盘的查询。磁盘的结构如下:

图1 .磁盘结构
磁盘主要有磁面,磁道,扇区,磁头的概念,它们的关系如下:
磁面:一个磁盘有很多个磁面
磁道:一个磁面有很多磁道
扇区:磁道与磁道之间构成扇区。
数据库的查询性能的快慢依赖于访问磁盘的速度。
要完成对磁盘的访问,从CPU发起指令访问磁盘(通过寻址)到磁头返回对应的地址的过程主要需要经过寄存器,内存,然后在到磁盘,指令给出要访问的地址,磁盘发起旋转,磁头找到相应的位置后就返回给内存,从而完成CPU读取数据的结果。这些步骤中,最耗时的操作的就是磁头从磁盘中找到地址。
多叉树
当内存需要获取磁盘的数据时,就发出一次寻址操作,寻址操作其实就是多叉树父节点查找子节点的过程。比如下图A到B的访问,就是一次寻址操作。

图2 .多叉树的访问
为了减少寻址次数,因此使用了多叉树而不使用二叉树,那是由于数据库具有大量数据,如果使用二叉树保存,层高会非常高,寻址次数会明显增多,从而查询数据的速度肯定会非常慢。
B树和B+树的概念
都知道数据库查询一般是非常快的,如果仅仅将数据存储在多叉树中而没有任何规律,那么是不可能的做到的,那么数据库的效率高其实就是有规律的多叉树,即B+树和B+树,如果一个M阶B树T,满足以下条件,就是一颗B树:
1. 每个结点至多拥有M课子树
2. 根结点至少拥有两颗子树
3. 除了根结点以外,其余每个分支结点至少拥有M/2课子树
4. 所有的叶结点都在同一层上
5. 有k课子树的分支结点则存在k-1个关键字,关键字按照递增顺序进行排序
6. 关键字数量满足ceil(M/2)-1 <= n <= M-1
比如 M = 6(6阶)B树
1.则B树最多有6棵子树,最多5个关键字(关键字比子树少1)
2.根结点最少可以有2棵子树(1个关键字)
3.关键字依次增加
4.关键字最少为2,最少子树为3.
5.叶子结点在同一层
以下是26个字母的一个B树:
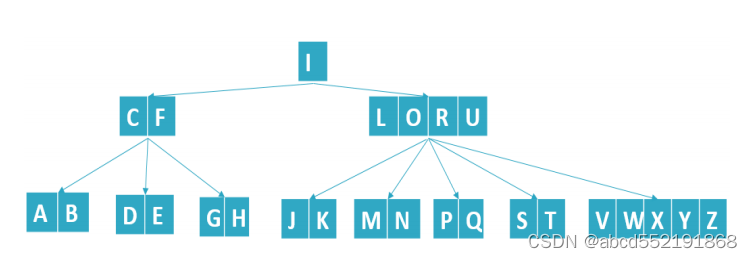
图3 B树的例子
数据库的数据结构不是使用的B树,而是使用的B+树,B+树与B树的区别在于:
- .B+树的数据只存储在叶子节点上,并且通过链表的方式将所有的叶子节点全部串联起来,而B树的数据存储在每一个节点上。
- B+树的子树数量等于它的关键字的数量,而B树是关键字数量加1。
- B+树的数据是存储在叶子节点上的,并且叶子节点的数据是双向链表关联起来,而B树的叶子节点各自独立。
B+树的内部节点只存放键,不存放值,因此一次读取,可以在内存页中获取更多的键,有利于更快地缩小查找范围。B+树的叶节点由一条链相连,因此,当需要进行一次全数据遍历的时候,B+树只需要使用O(logN)时间找到最小的一个节点,然后通过链进行O(N)的顺序遍历即可,而B树则需要对树的每一层进行遍历,这会需要更多的内存置换次数,因此也就需要花费更多的时间。
B+树同时支持随机检索和顺序检索,而B树只适合随机检索。B+树空间利用率更高,可减少I/O次数,磁盘读写代价更低。B+树的内部结点并没有指向关键字具体信息的指针,只是作为索引使用,其内部结点比B树小,盘块能容纳的结点中关键字数量更多,一次性读入内存中可以查找的关键字也就越多,相对的,IO读写次数也就降低了。
B树的操作
对一个树的操作,无非就是增删改查。即B树的添加,B树的删除,B树的修改(节点的修改,我们不关心这个操作,这个操作无非就是根据key查询之后,对value进行修改),和B树的查询。
B树的添加
为了更好的说明B树节点添加的操作,我们假如以依次添加26个字母为例,B树节点的key最大值为5来进行说明,首先我们看看添加A到E

图4 B树添加A到E
在插入ABCDE的时候,由于当前就一个节点,并且key还没有超过5个,直接插入即可。
接下来我们插入F,插入F如下图所示
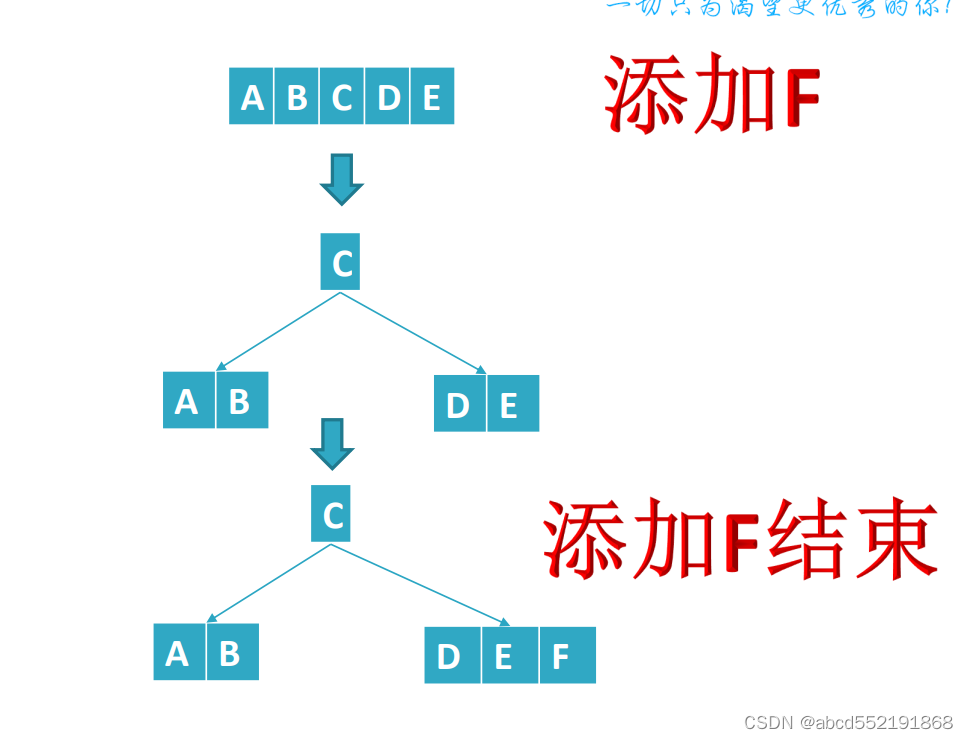
图5 插入关键字F
在插入F之前,只有1个节点,并且节点的key已经满了,无法在继续插入key,那么必然要增加节点,这里就涉及到节点的分裂操作。其实节点的插入无非就2个操作:找到要插入的位置和必要的分裂操作。
插入节点
插入节点一般是在叶子节点上,理论上插入到内节点也是可以的。不过插入到内节点操作上会有很多的不便,代码实现起来也比较复杂。
假如在插入的过程中,已经找到要插入的叶子节点,如果叶子节点的关键码个数没有达到上限,可以直接插入;如果达到了上限,就要分裂成两个子节点,并把中间的关键码往上放到父节点中。在节点的key往父节点移动的过程中,父亲节点的key也会随着增多,假如父节点的key也满了,则需要再次分裂父节点,直到达到B树的平衡。
节点的插入是从根节点开始的,假如在找到具体的叶子节点之前,可能会出现内节点和最终的叶子节点的key满的情况,在出现节点满的情况,需要分裂节点。节点的分裂需要分为2种情况:一种情况是分裂根节点,如上图中添加F的情况,另一种就是不是分裂根情况的节点,比如下图添加I的情况,由于存在父节点,因此不需要像根节点分裂一样,需要生成一个新根节点来作为分裂节点的父节点。

图 6 插入关键字I
根节点分裂比非根节点分裂多了2个步骤:
(1)生成一个新节点,并将这个新节点作为树的根节点
(2)将之前的根节点作为这个新节点的第一个孩子。
根节点和非根节点后续的分裂步骤都一样,主要包括以下步骤
1.创建一个新节点z
2.将分裂节点的后半部分key值赋值给z
3.如果分裂的结点是内结点,则还需要将分裂结点的子树赋值给z
4.将分裂节点的中间key移动到父亲节点的合适位置,并将父节点的节点插入key之后的指针后移。
5.分裂节点的数量减少
6.分裂节点的父节点的key+1和num值的修改
B树的删除
B树的添加会导致节点的分裂,从而形成一颗巨大的多叉树,B树的删除(即节点的删除)会导致节点的合并,从而让树的规模逐渐变小。在说明具体什么时候会导致节点合并之前,先看看删除节点A的情况
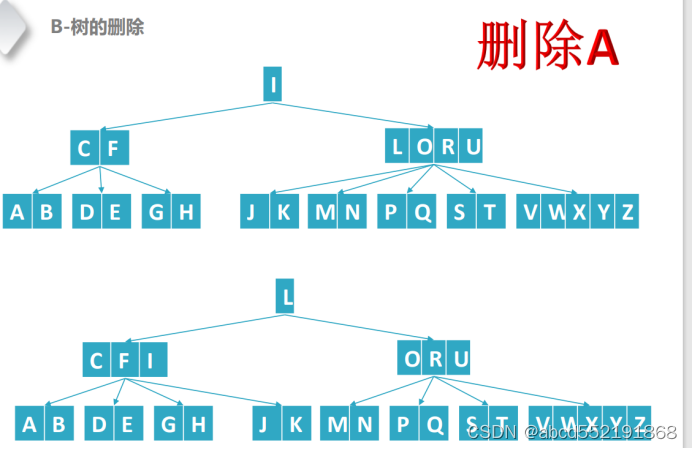
图 7 删除A节点,往右借用节点
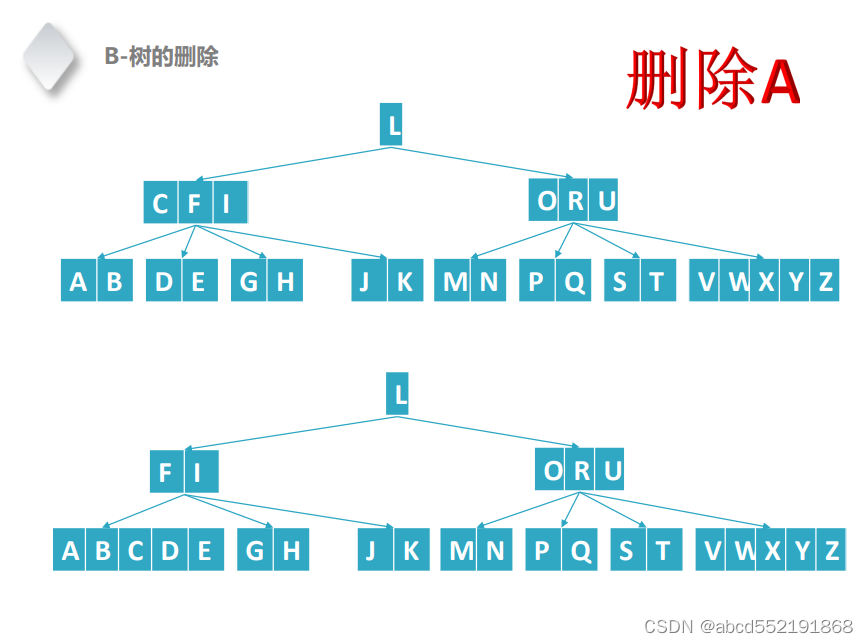
图 8 删除A节点,将父节点合并到关键字A和关键字D的节点之间
删除A需要从邻居借用子树和合并节点,在第一幅图中,关键字key A所在的节点的像邻居借用了关键字key JK所在的节点。在第二幅图中,关键字A所在的节点的父节点的关键字C移动到了关键字A的节点,然后并和关键字D和E所在的所在的节点进行合并。
合并操作
为什么需要合并呢,这是因为如果遇到一个结点的关键字key(key < M/2 -1,其中M是子树的 个数)值很少,那么就会出现很复杂的情况,导致不满足B树的情形。如上图删除A的过程中,合并节点会出现节点下沉的情况,删除操作也是删除叶子节点,因此如果删除的是内节点,也会让内节点先合并下沉,然后进行删除。
合并的流程主要如下:
1.根据合并节点的位置,找到父节点要下移的key,比如上面删除A,由于属于父节点的第一个孩子,就需要将第一个key下移。
2.然后如果下移的key与要删除key的节点进行合并,然后并和相邻的节点进行合并。
借用操作
1.将父节点的第一个关键字移动到某个子树
2.如果是往左边子树借用节点,就将左边子树节点的最后一个关键字移动到父节点,如果是往右边子树借用节点,就将右边子树的节点的第一个关键字移动到父亲节点
3.对于第2步,如果是往右边子树借用节点,就将右边子树的节点的第一个关键字作为左边子树的最后一个关键字,如果往左边子树借用节点,就将左边子树的节点的最后一个关键字作为右边子树的第一个关键字。
删除节点
删除节点可能会涉及到如下过程:
1.如果要删除的相邻两颗子树的key,都小于或者等于M/2-1(M为节点子树的个数),那么就要进行合并,这是因为邻居节点借用节点之后,会导致邻居不满足节点key的最小值条件)
2.左边子树大于M/2 -1, 往左边子树借用结点
3.右边子树大于M/2-1, 往右边子树借用节点
4.直接删除节点的key
一般在删除节点时,都会自上而下的判断节点的key的数量是否小于M/2,如果是,都会做合并子树和从相邻节点中借用节点,而不是仅仅在删除的节点做这样的操作。这样的目的是为了防止节点删除出现很复杂的情况。
B树的查询
从根节点开始查询,然后对根节点使用二分查找可以达到hlog(n)的时间复杂度,比如查找图3的Q,从根节点开始查询,然后往右开始查询,每次查询到节点的时候,都是用二分查找。
代码实现
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <assert.h>
#define DEGREE 3
typedef int KEY_VALUE;
//不需要父指针,因为节点增加都是从上而下的,不需要指向父亲
typedef struct _btree_node {
KEY_VALUE *keys; //节点key 最多为DEGREE * 2 -1
struct _btree_node **childrens; //孩子指针,最多个数为 2 * DEGREE
int num; //节点的key个数
int leaf;//是否是叶子节点,0-否,1-是
} btree_node;
typedef struct _btree {
btree_node *root;//根节点
int t;//度,--->DEGREE
} btree;
//创建一个节点 t->度,leaf->是否为叶子节点
btree_node *btree_create_node(int t, int leaf) {
btree_node *node = (btree_node*)calloc(1, sizeof(btree_node));
if (node == NULL) assert(0);
node->leaf = leaf;
node->keys = (KEY_VALUE*)calloc(1, (2*t-1)*sizeof(KEY_VALUE)); //生成2 * t -1 存放key的空间
node->childrens = (btree_node**)calloc(1, (2*t) * sizeof(btree_node*));//声明 2*t个孩子节点指针空间
node->num = 0; //当前不存在key
return node;
}
void btree_destroy_node(btree_node *node) {
assert(node);
free(node->childrens);
free(node->keys);
free(node);
}
//创建树,无非就是创建一个根节点,并赋予孩子的degree
void btree_create(btree *T, int t) {
T->t = t;
btree_node *x = btree_create_node(t, 1);
T->root = x;
}
/// @brief 分裂节点(分裂节点是用于插入节点的,由于插入节点是自上而下的,因此如果找到某个节点已满,就需要分裂,如果分裂到孩子节点了,说明父节点都不是满的)
/// @param T 树
/// @param x 要分裂节点的父节点
/// @param i 哪个孩子要分裂(孩子序号从0开始)
void btree_split_child(btree *T, btree_node *x, int i) {
int t = T->t;
btree_node *y = x->childrens[i];//y要分裂的节点
btree_node *z = btree_create_node(t, y->leaf);//生成一个新节点,用于保存y指点后半部分的节点(注意,如果DEGREE为3,那么就是最多5个key,最后2个key放到这个新生成的节点)
z->num = t - 1;
int j = 0;
for (j = 0;j < t-1;j ++) {
z->keys[j] = y->keys[j+t];//赋值新节点的key
}
if (y->leaf == 0) {//如果不是叶子节点,还需要将分类节点的孩子放到新节点种
for (j = 0;j < t;j ++) {
z->childrens[j] = y->childrens[j+t];
}
}
y->num = t - 1;//设置分裂节点后的节点数目
for (j = x->num;j >= i+1;j --) {//父节点要插入节点之后的所有节点的孩子节点都后移
x->childrens[j+1] = x->childrens[j];//
}
x->childrens[i+1] = z;//第i个节点为要插入的位置,i+1个为要插入的孩子节点
for (j = x->num-1;j >= i;j --) {//要插入位置的所有key后移
x->keys[j+1] = x->keys[j];
}
x->keys[i] = y->keys[t-1];
x->num += 1;
}
/// @brief 树节点key没有满的时候插入
/// @param T 要插入的树
/// @param x 要插入的节点的父亲节点或者作为叶子节点插入
/// @param k
void btree_insert_nonfull(btree *T, btree_node *x, KEY_VALUE k) {
int i = x->num - 1;//
if (x->leaf == 1) {//要插入的节点是叶子节点
while (i >= 0 && x->keys[i] > k) {//找到要插入的位置
x->keys[i+1] = x->keys[i];
i --;
}
x->keys[i+1] = k;//指定的位置插入
x->num += 1;
} else {//要插入的位置不是叶子节点
while (i >= 0 && x->keys[i] > k) i --;//找到要插入的位置
if (x->childrens[i+1]->num == (2*(T->t))-1) {//如果要插入的节点已满,就需要分裂该节点
btree_split_child(T, x, i+1);//key要插入的节点已满,需要分裂节点
if (k > x->keys[i+1]) i++;//判断key要插入节点的左边部分还是插入到右边部分,如果关键字比i+i(右边部分的key)大,就插入到右边部分
}
btree_insert_nonfull(T, x->childrens[i+1], k);//插入待插入的节点
}
}
void btree_insert(btree *T, KEY_VALUE key) {
//int t = T->t;
btree_node *r = T->root;
if (r->num == 2 * T->t - 1) {//根节点分裂
btree_node *node = btree_create_node(T->t, 0);//新创建的节点作为父节点
T->root = node;
node->childrens[0] = r;//作为根的0号节点
btree_split_child(T, node, 0); //分裂根的0号节点
int i = 0;
if (node->keys[0] < key) i++;//判断要插入的节点是插入到到0号子树还是1号子树
btree_insert_nonfull(T, node->childrens[i], key);
} else {//根节点 未满 ,就直接插入
btree_insert_nonfull(T, r, key);
}
}
void btree_traverse(btree_node *x) {
int i = 0;
for (i = 0;i < x->num;i ++) {//
if (x->leaf == 0) //非叶子节点
btree_traverse(x->childrens[i]);
printf("%C ", x->keys[i]);
}
if (x->leaf == 0) btree_traverse(x->childrens[i]);
}
void btree_print(btree *T, btree_node *node, int layer)
{
btree_node* p = node;
int i;
if(p){
printf("\nlayer = %d keynum = %d is_leaf = %d\n", layer, p->num, p->leaf);
for(i = 0; i < node->num; i++)
printf("%c ", p->keys[i]);
printf("\n");
#if 0
printf("%p\n", p);
for(i = 0; i <= 2 * T->t; i++)
printf("%p ", p->childrens[i]);
printf("\n");
#endif
layer++;
for(i = 0; i <= p->num; i++)
if(p->childrens[i])
btree_print(T, p->childrens[i], layer);
}
else printf("the tree is empty\n");
}
//二分查询节点的位置
int btree_bin_search(btree_node *node, int low, int high, KEY_VALUE key) {
int mid;
if (low > high || low < 0 || high < 0) {
return -1;
}
while (low <= high) {
mid = (low + high) / 2;
if (key > node->keys[mid]) {
low = mid + 1;
} else {
high = mid - 1;
}
}
return low;
}
//{child[idx], key[idx], child[idx+1]}
void btree_merge(btree *T, btree_node *node, int idx) {
btree_node *left = node->childrens[idx];
btree_node *right = node->childrens[idx+1];
int i = 0;
/data merge
left->keys[T->t-1] = node->keys[idx];
for (i = 0;i < T->t-1;i ++) {
left->keys[T->t+i] = right->keys[i];
}
if (!left->leaf) {
for (i = 0;i < T->t;i ++) {
left->childrens[T->t+i] = right->childrens[i];
}
}
left->num += T->t;
//destroy right
btree_destroy_node(right);
//node
for (i = idx+1;i < node->num;i ++) {
node->keys[i-1] = node->keys[i];
node->childrens[i] = node->childrens[i+1];
}
node->childrens[i+1] = NULL;
node->num -= 1;
if (node->num == 0) {
T->root = left;
btree_destroy_node(node);
}
}
void btree_delete_key(btree *T, btree_node *node, KEY_VALUE key) {
if (node == NULL) return ;
int idx = 0, i;
while (idx < node->num && key > node->keys[idx]) {//找到要删除节点的位置
idx ++;
}
if (idx < node->num && key == node->keys[idx]) {//节点中找到要删除的key
if (node->leaf) { //叶子节点
for (i = idx;i < node->num-1;i ++) {
node->keys[i] = node->keys[i+1];
}
node->keys[node->num - 1] = 0;
node->num--;
if (node->num == 0) { //root
free(node);
T->root = NULL;
}
return ;
} else if (node->childrens[idx]->num >= T->t) {
btree_node *left = node->childrens[idx];
node->keys[idx] = left->keys[left->num - 1];
btree_delete_key(T, left, left->keys[left->num - 1]);
} else if (node->childrens[idx+1]->num >= T->t) {
btree_node *right = node->childrens[idx+1];
node->keys[idx] = right->keys[0];
btree_delete_key(T, right, right->keys[0]);
} else {
btree_merge(T, node, idx);
btree_delete_key(T, node->childrens[idx], key);
}
} else {//节点中没有找到要删除的key
btree_node *child = node->childrens[idx];//继续寻找孩子
if (child == NULL) { //没有找到对应的孩子
printf("Cannot del key = %d\n", key);
return ;
}
if (child->num == T->t - 1) {
btree_node *left = NULL;
btree_node *right = NULL;
if (idx - 1 >= 0)
left = node->childrens[idx-1];
if (idx + 1 <= node->num)
right = node->childrens[idx+1];
if ((left && left->num >= T->t) ||
(right && right->num >= T->t)) {
int richR = 0;
if (right) richR = 1;
if (left && right) richR = (right->num > left->num) ? 1 : 0;
if (right && right->num >= T->t && richR) { //borrow from next
child->keys[child->num] = node->keys[idx];
child->childrens[child->num+1] = right->childrens[0];
child->num ++;
node->keys[idx] = right->keys[0];
for (i = 0;i < right->num - 1;i ++) {
right->keys[i] = right->keys[i+1];
right->childrens[i] = right->childrens[i+1];
}
right->keys[right->num-1] = 0;
right->childrens[right->num-1] = right->childrens[right->num];
right->childrens[right->num] = NULL;
right->num --;
} else { //borrow from prev
for (i = child->num;i > 0;i --) {
child->keys[i] = child->keys[i-1];
child->childrens[i+1] = child->childrens[i];
}
child->childrens[1] = child->childrens[0];
child->childrens[0] = left->childrens[left->num];
child->keys[0] = node->keys[idx-1];
child->num ++;
node->key[idx-1] = left->keys[left->num-1];
left->keys[left->num-1] = 0;
left->childrens[left->num] = NULL;
left->num --;
}
} else if ((!left || (left->num == T->t - 1))
&& (!right || (right->num == T->t - 1))) {
if (left && left->num == T->t - 1) {
btree_merge(T, node, idx-1);
child = left;
} else if (right && right->num == T->t - 1) {
btree_merge(T, node, idx);
}
}
}
btree_delete_key(T, child, key);
}
}
int btree_delete(btree *T, KEY_VALUE key) {
if (!T->root) return -1;
btree_delete_key(T, T->root, key);//从根节点开始判断是否应该删除
return 0;
}
int main() {
btree T = {0};
btree_create(&T, 3);//创建key最大个数为5个B树
srand(48);
int i = 0;
char key[26] = "ABCDEFGHIJKLMNOPQRSTUVWXYZ";
for (i = 0;i < 26;i ++) {
//key[i] = rand() % 1000;
printf("%c ", key[i]);
btree_insert(&T, key[i]);
}
btree_print(&T, T.root, 0);
for (i = 0;i < 26;i ++) {
printf("\n---------------------------------\n");
btree_delete(&T, key[25-i]);
//btree_traverse(T.root);
btree_print(&T, T.root, 0);
}
}
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 黑马程序员——html css基础——day02——HTML进阶
- 小白入门之安装Navicat
- 部署了SSL证书,为什么还会出现不安全的提示?
- MongoDB ReplicaSet 部署
- ffmpeg批量转换wav为mp3
- kubeadm创建k8s集群
- [Kubernetes]9. K8s ingress讲解借助ingress配置http,https访问k8s集群应用
- C++ STL泛型算法
- 遥感论文 | Scientific Reports | 一种显著提升遥感影像小目标检测的网络!
- 基于matlab实现雷达信号采集数据处理(时频谱图)附Matlab仿真