【高等数学之定积分】
发布时间:2024年01月16日
一、什么是定积分?
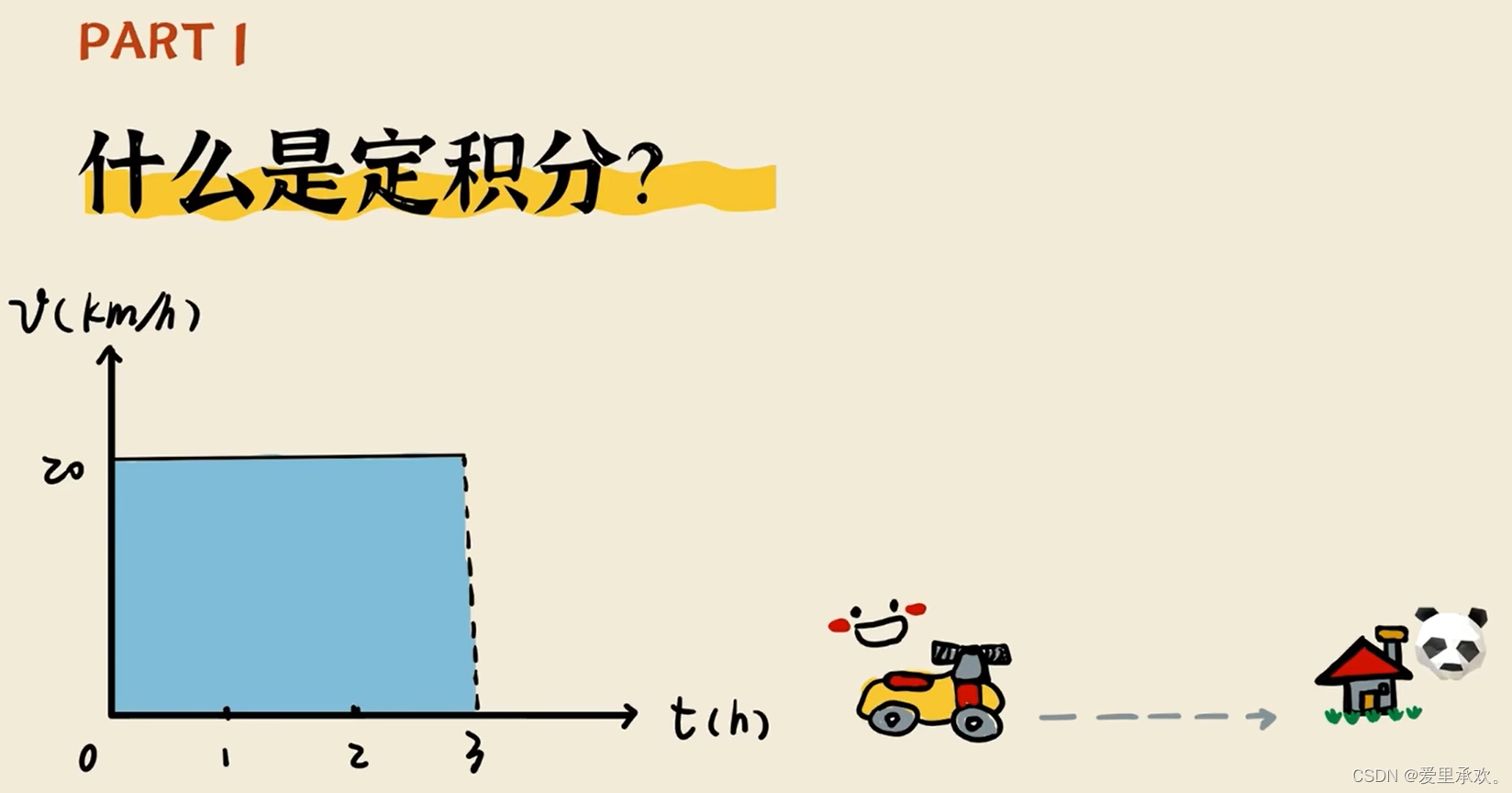
我们可以先结合物理来分析一下,我们第一次从家出发,第一次开车是新手小白,所以我们十分谨慎,基本保持匀速行驶,这种情况下我们的路程大小是怎么样的呢?
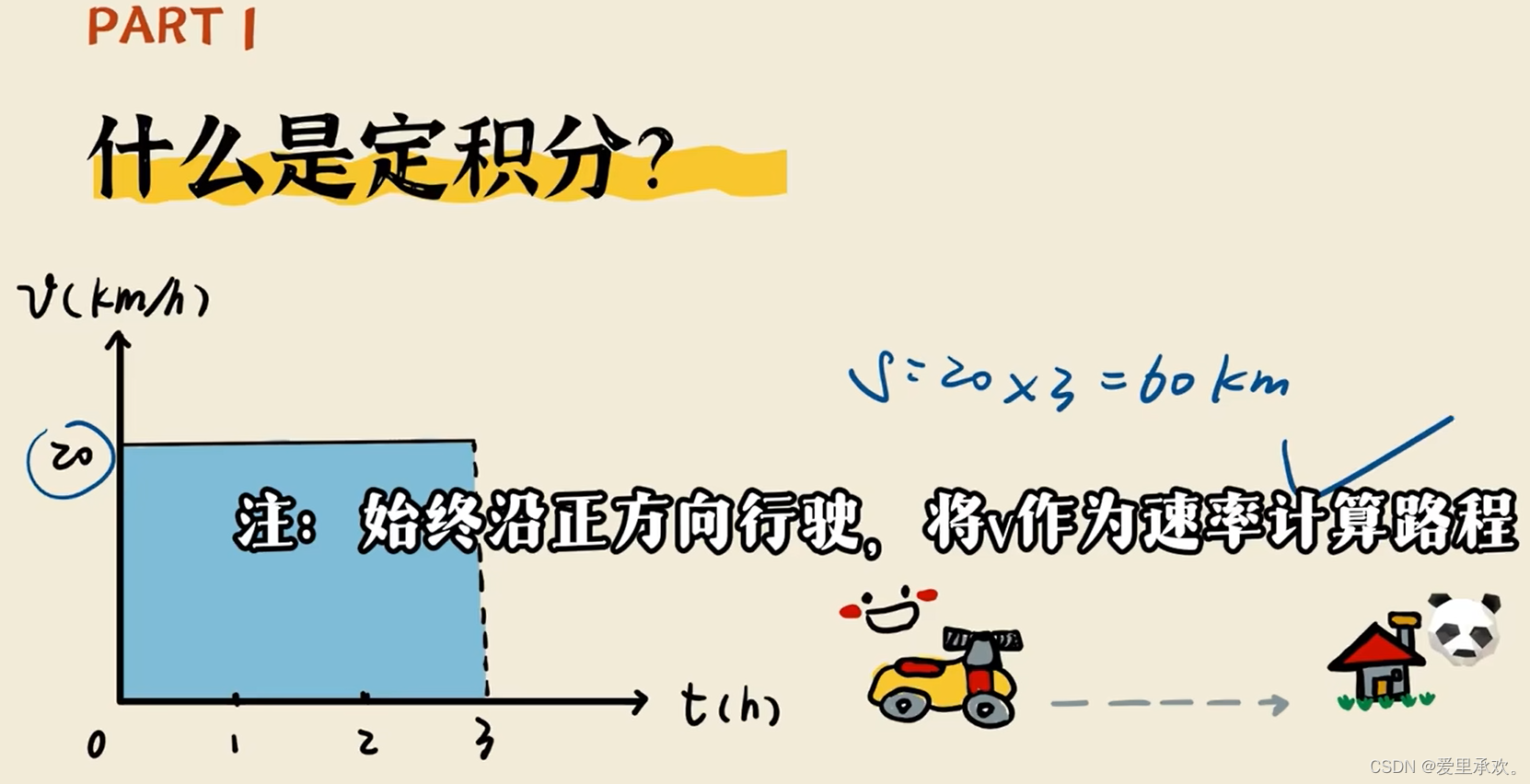
第二次开车我们已经驾轻就熟,我们可以在不同的路段用不同的行驶速度了,那么这种情况下我们的路程又是什么情况?(借鉴Kira老师)
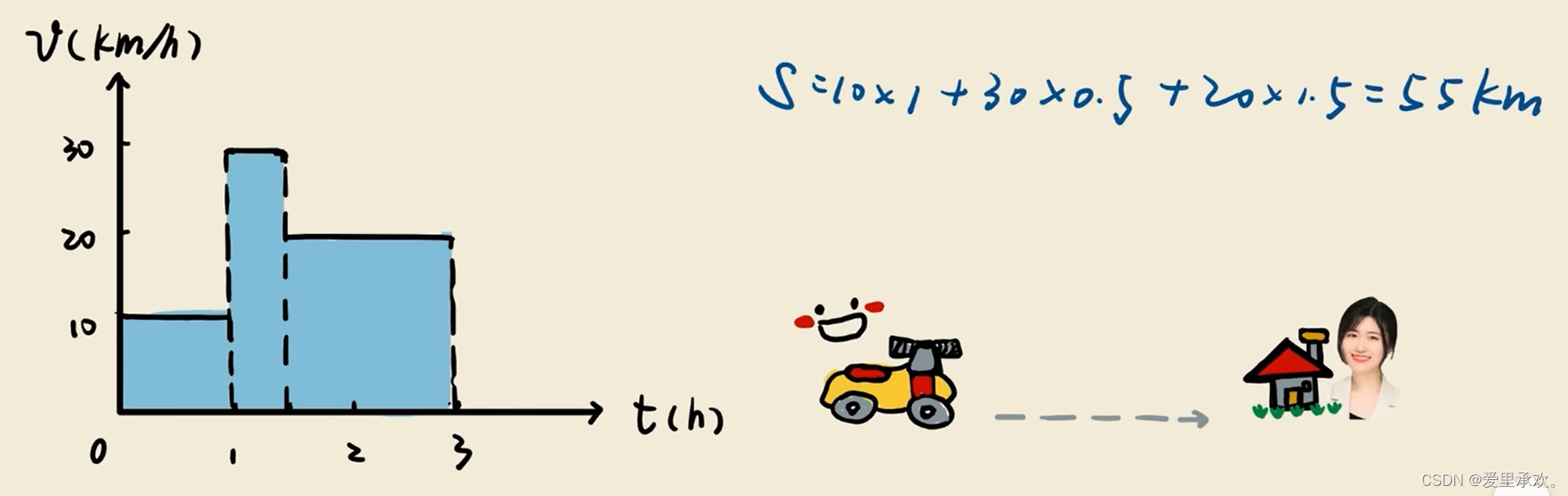
第三次我们已经是老司机了,可以灵活的变速,那么行驶路程如下:
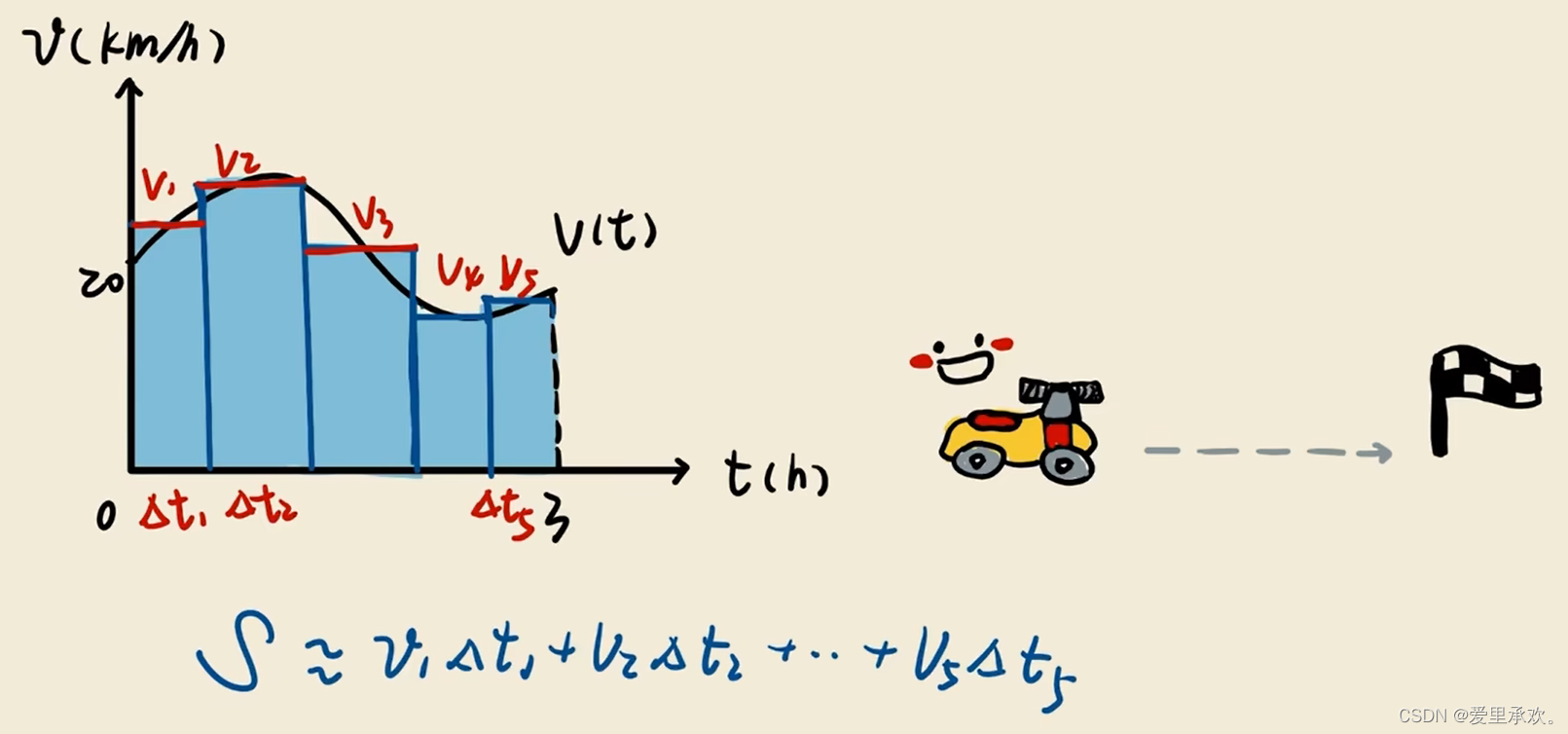
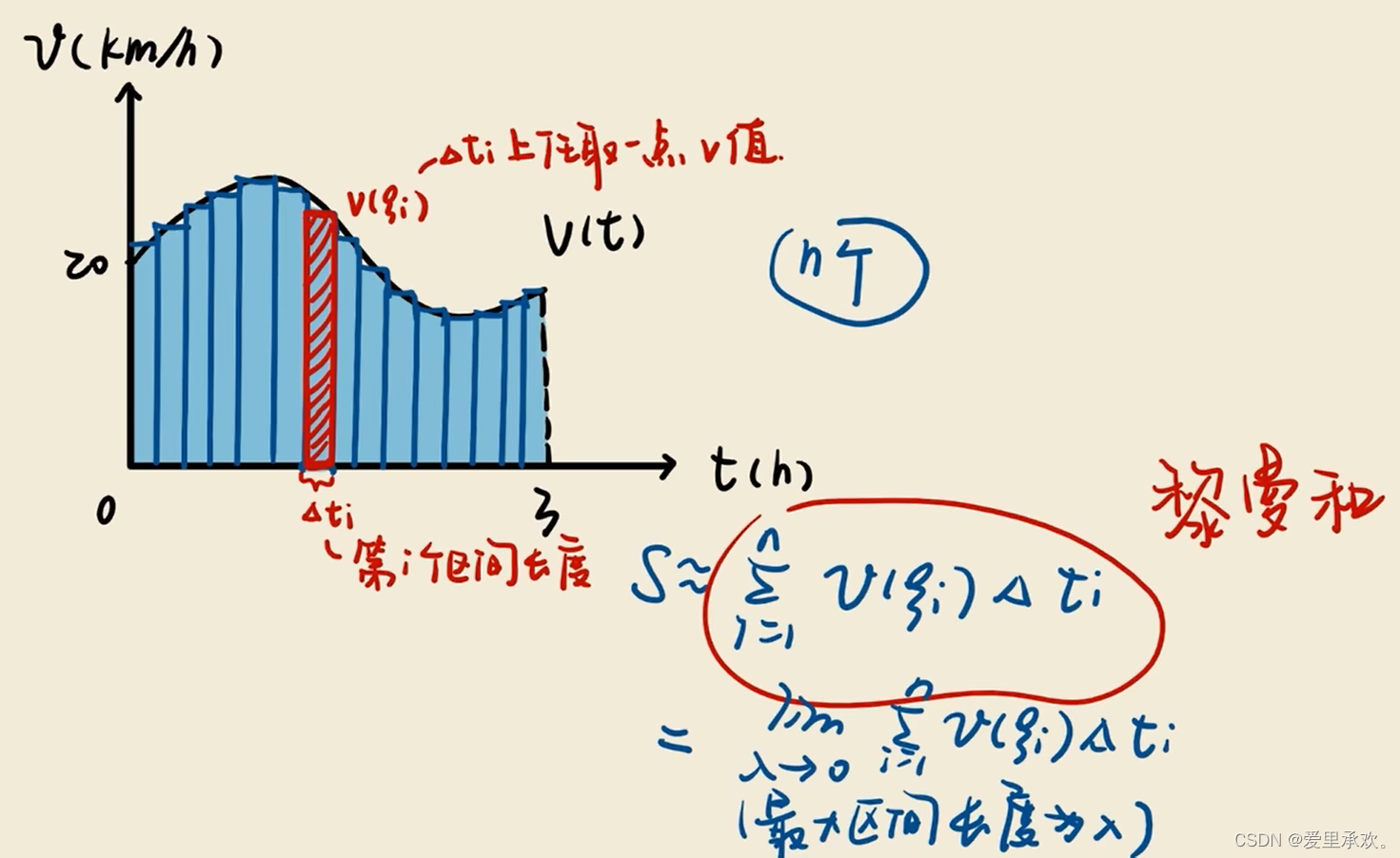
由此我们将取每一块小区间,把曲线分割成无数个小矩形块,从而引出了黎曼和的表达形式。
1.1、定积分的定义
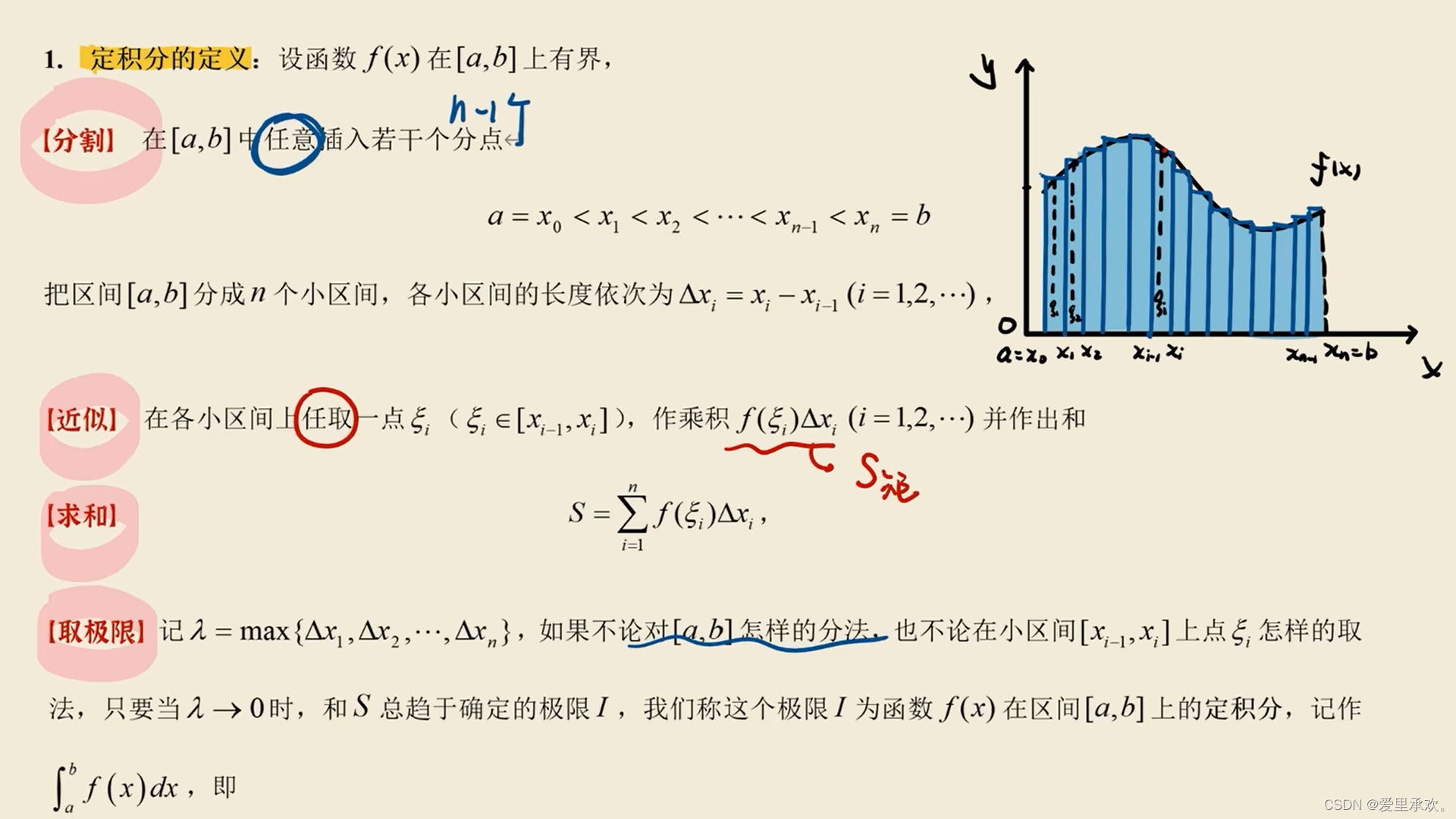
由上图我们看到可以将定积分求解过程分成四个部分,分别是:分割、近似、求和、取极限。定积分的公式从右到左依次也是如此排列的。

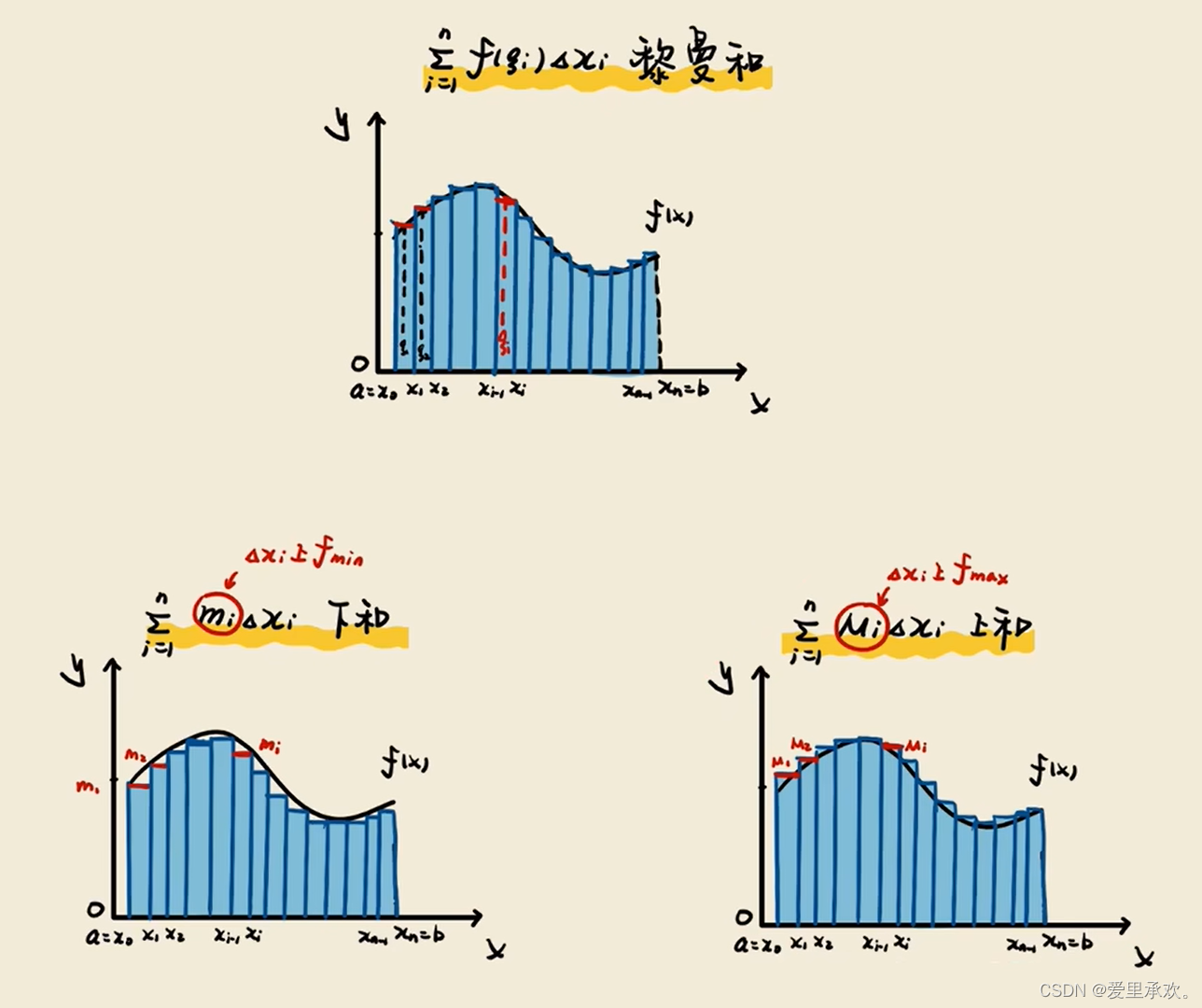 我们又可以将黎曼和分成两种,分别是黎曼上和以及黎曼下和,其实也就是一个取区间最大值,另一个取区间最小值。
我们又可以将黎曼和分成两种,分别是黎曼上和以及黎曼下和,其实也就是一个取区间最大值,另一个取区间最小值。
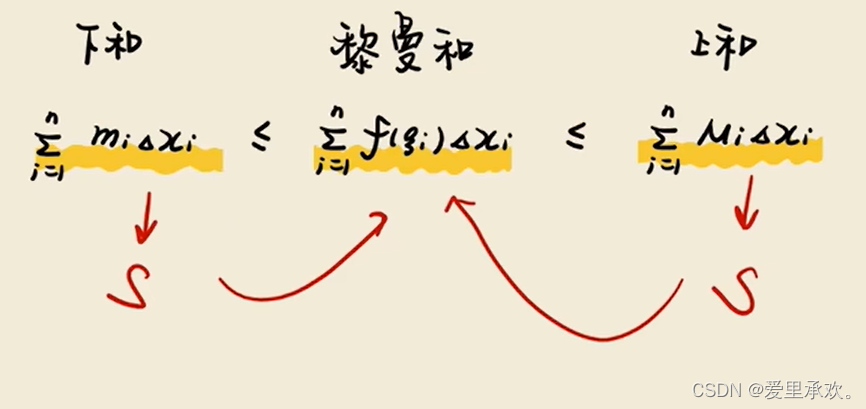
无论黎曼和的ξ取哪一个数值,均可以被上、下和夹逼,从而得到一样的值。
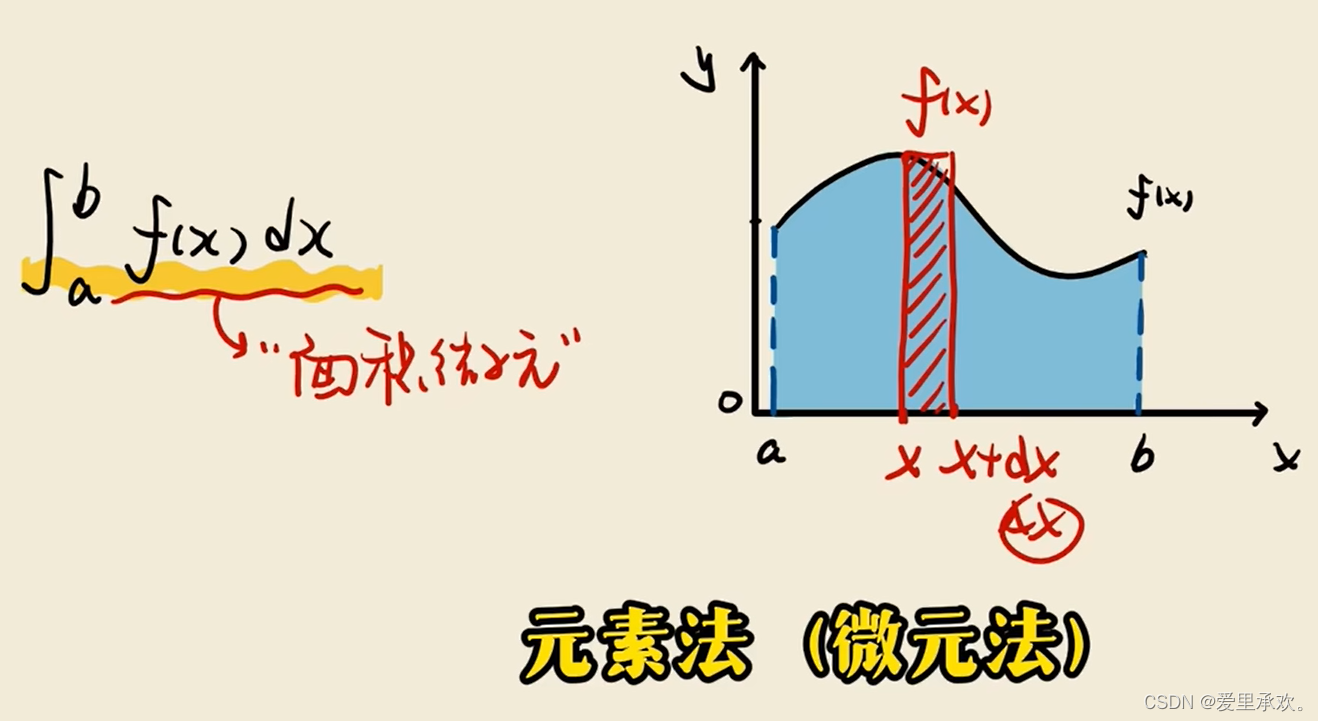
通常求取定积分利用元素法也就是微元法,f(x)dx就是每一个矩形面积的微元。?
小exercise:



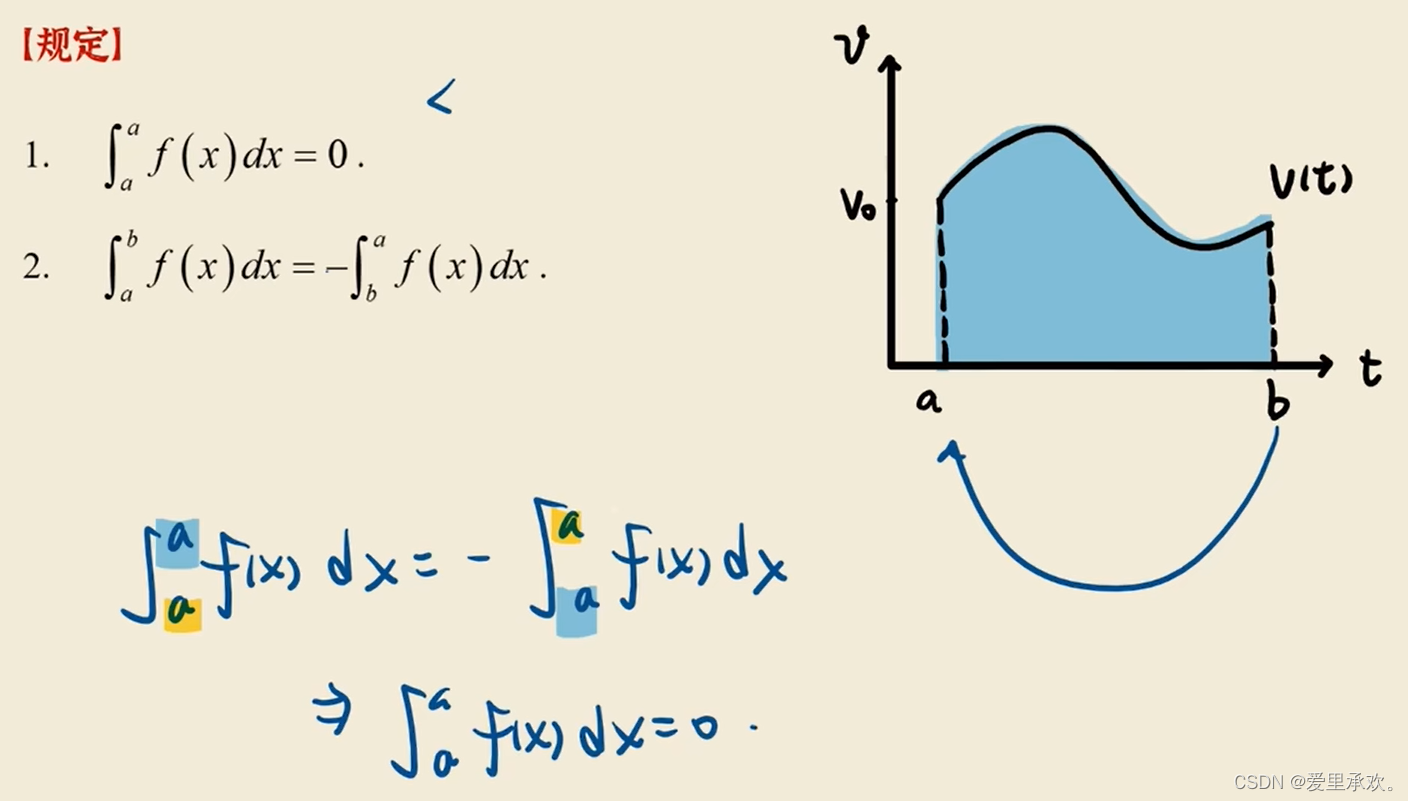
1.2、定积分的几何意义
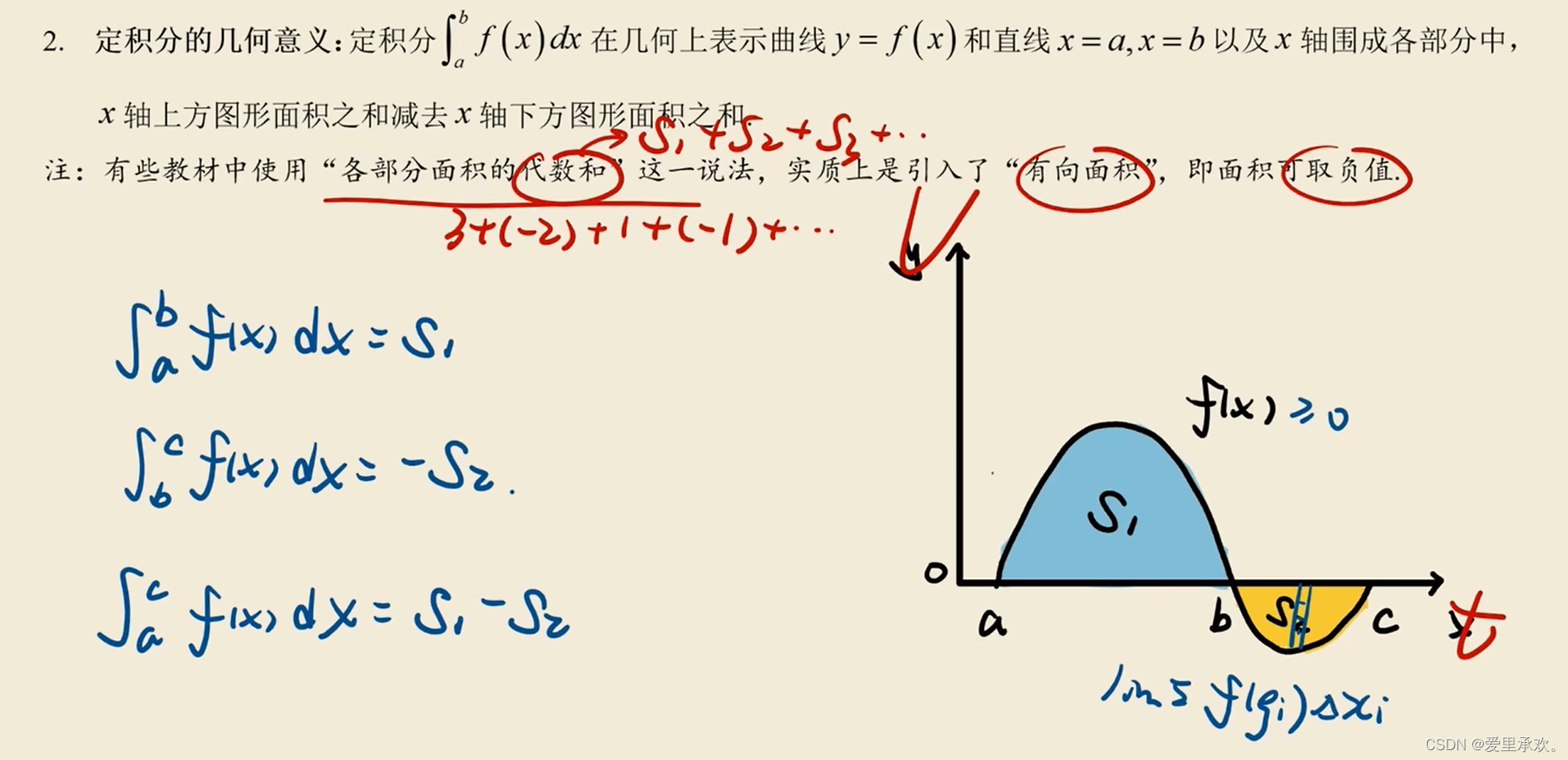

二、常见的可积函数类



有界我们可以利用可积来推出,可积其实也变相说明了极限存在,极限存在也即有界。?

三、用定积分求n项和数列极限

数列极限我们可以试试反推,将数列极限的表达式逆推到近似上图的定积分表达形式中。



不要看评论区,看这(上图)!!!
四、定积分的基本性质(5个)

4.1、性质1?
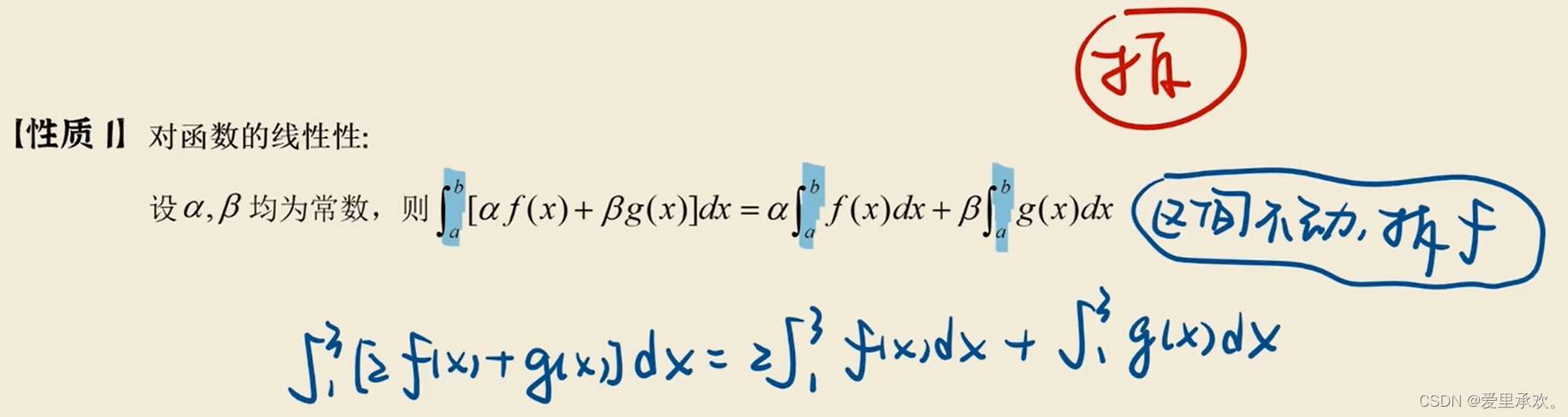
4.2、性质2
4.3、性质3
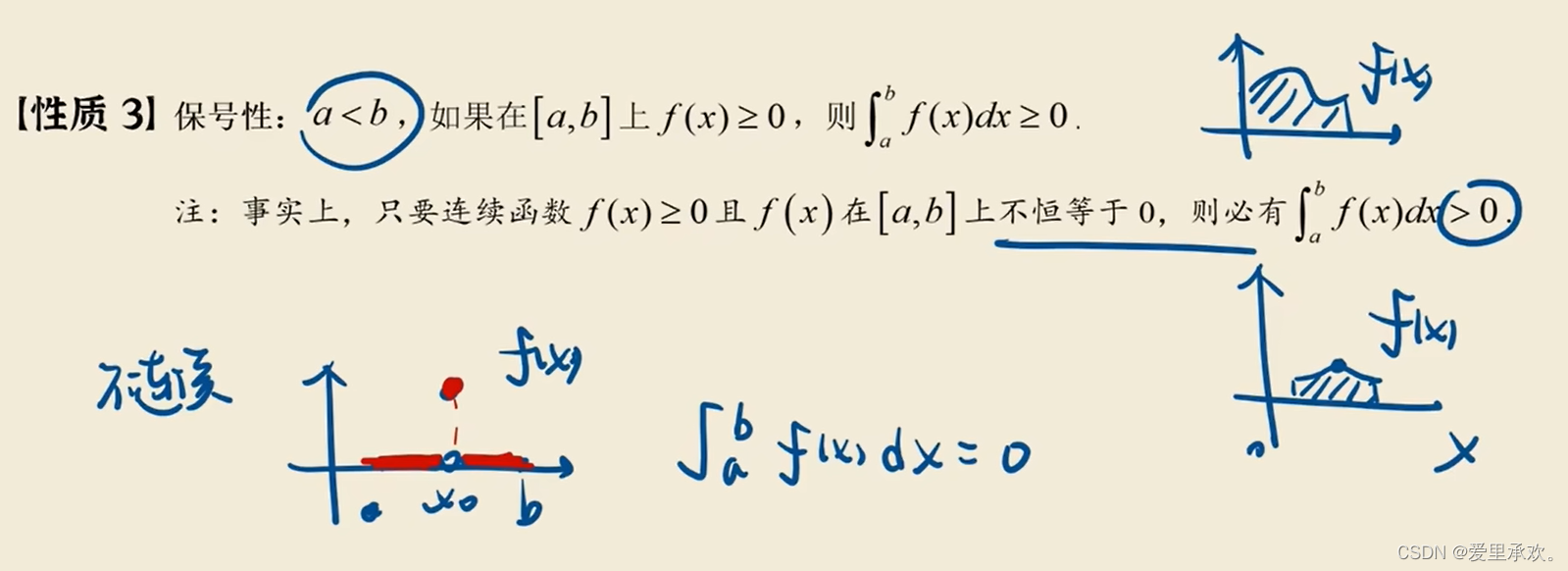
4.3.1、推论1

 4.3.2、推论2
4.3.2、推论2
 4.4、性质4
4.4、性质4


4.5、性质5?


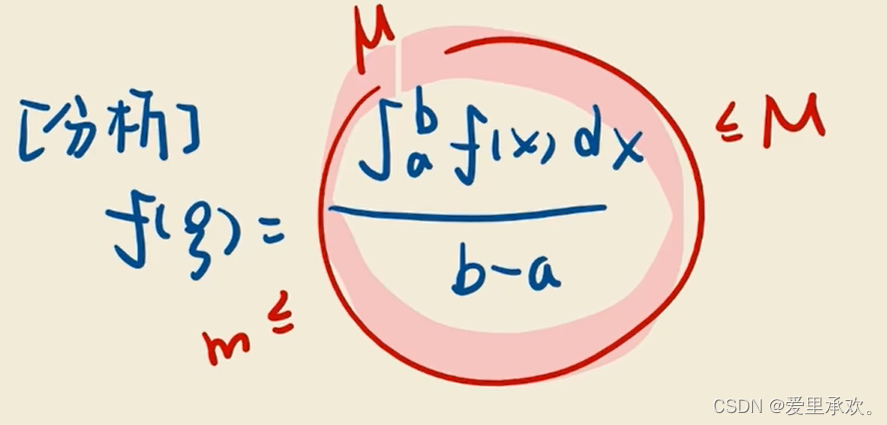

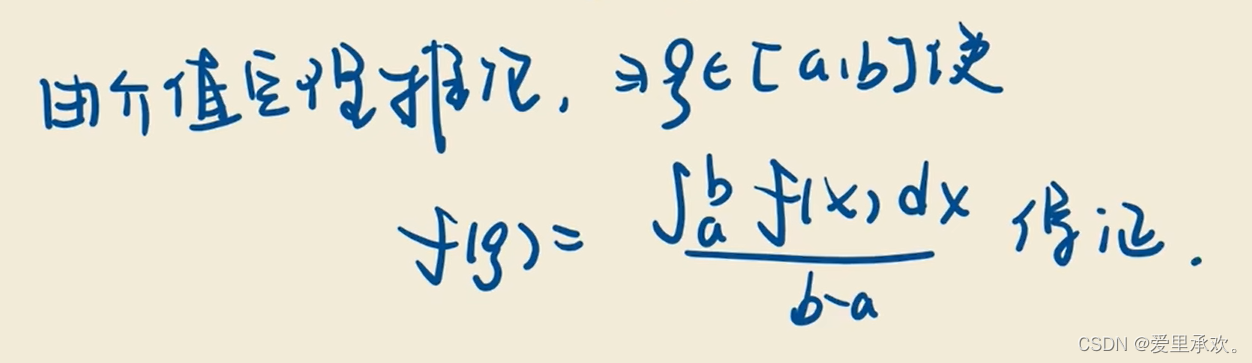

五、深入定积分?
5.1、以旧引新思?
从下图可以看出,如果想要求速度在一段时间内的积分,还可以用路程相减求得,我们还知道路程的导数是速度,对平均速率求极限就是导数的定义,同时也是瞬时速度,那就可以知道对速率求积分就是我们想要的路程。(实例2与实例1同理)?

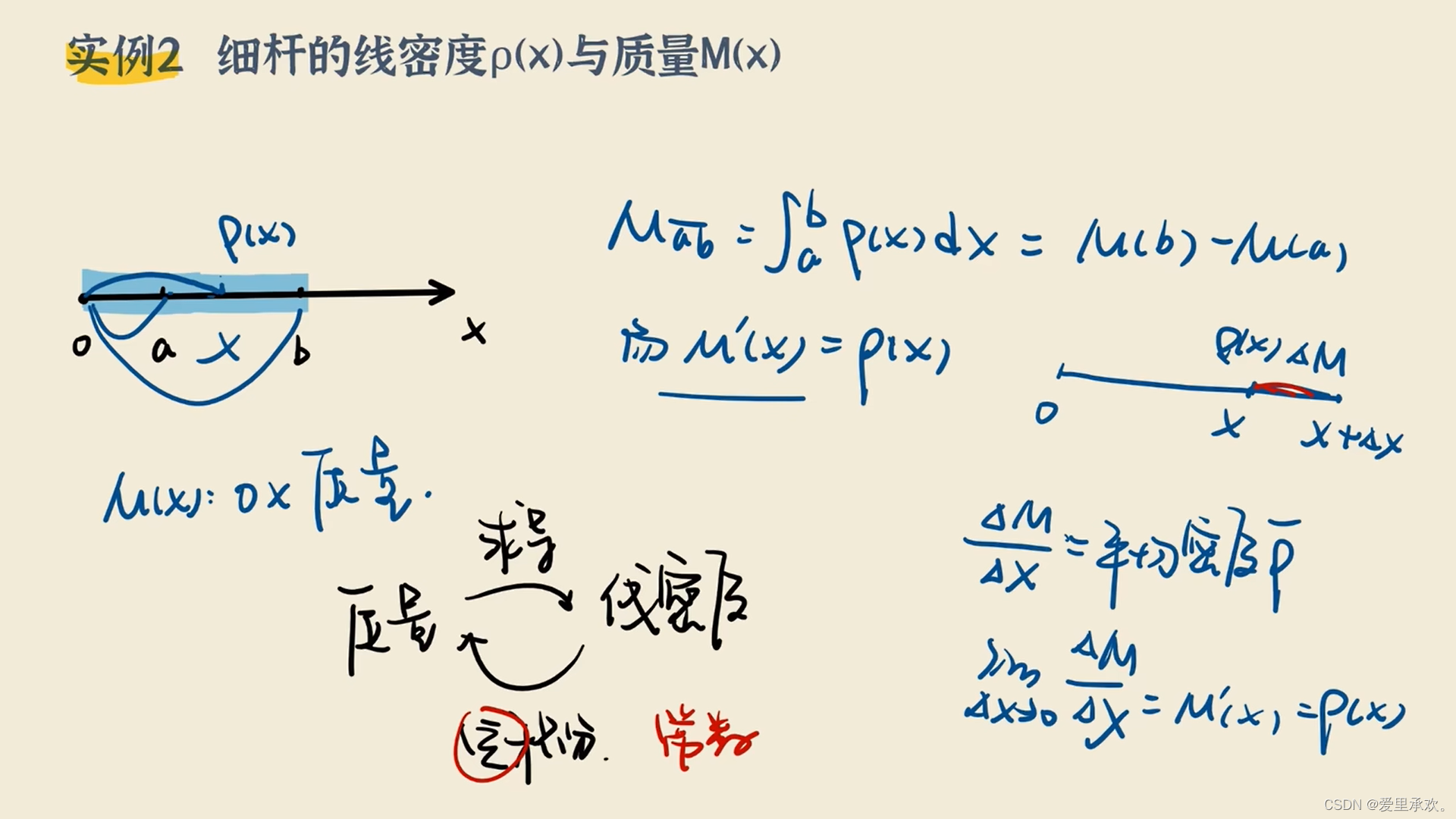
5.2、牛顿眼里的面积
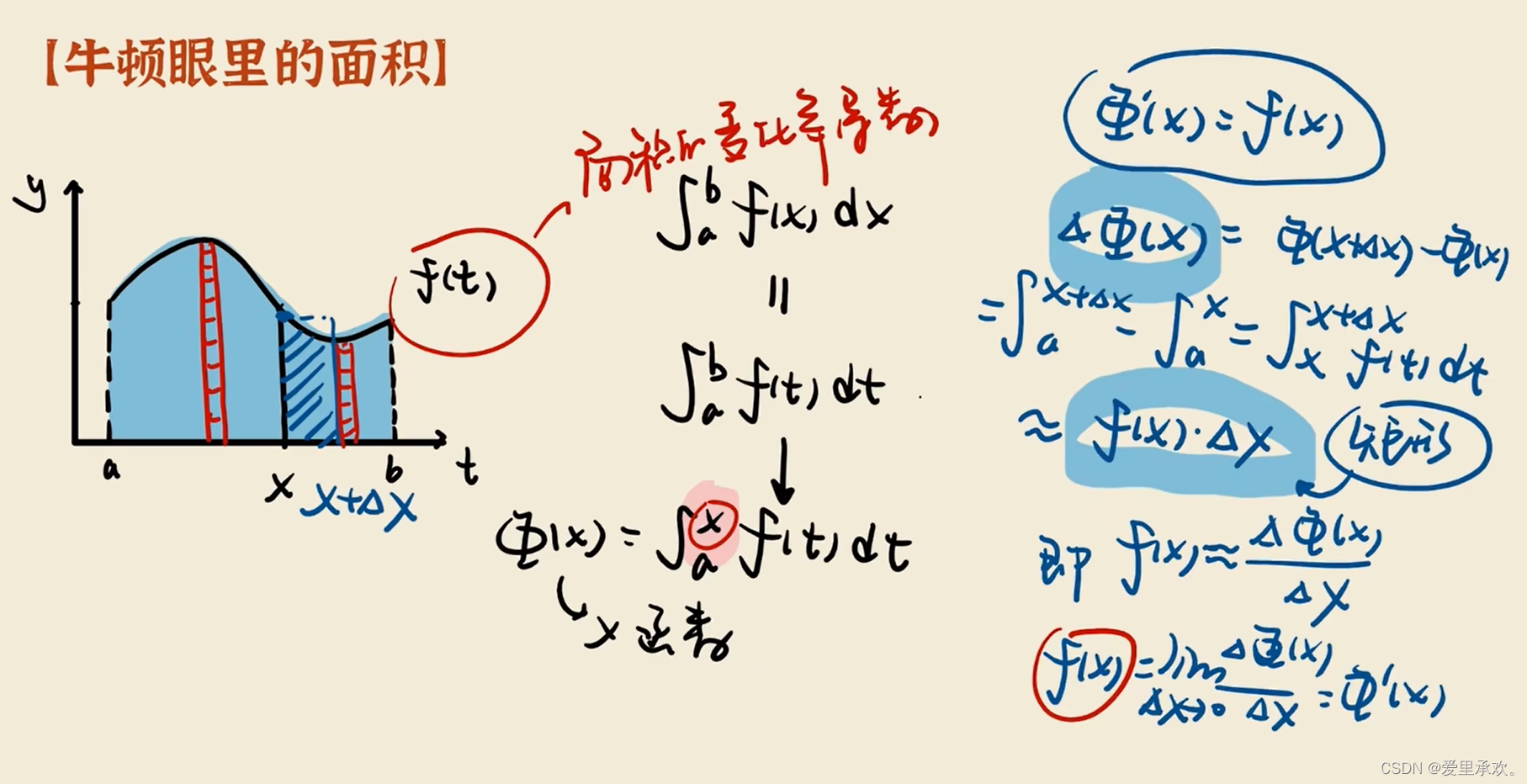
六、积分限的函数(变限积分)
6.1、定义



6.2、变限积分求导


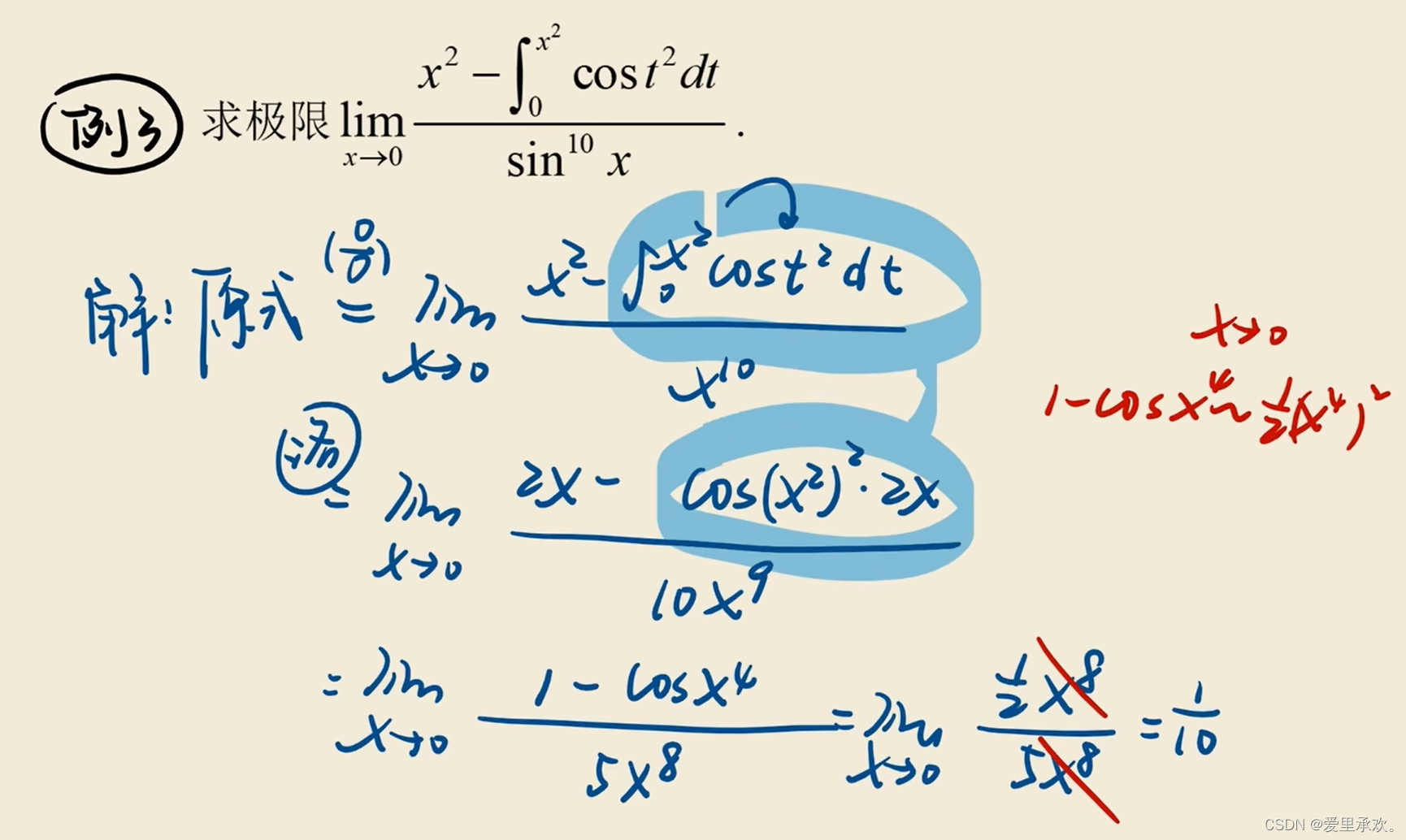

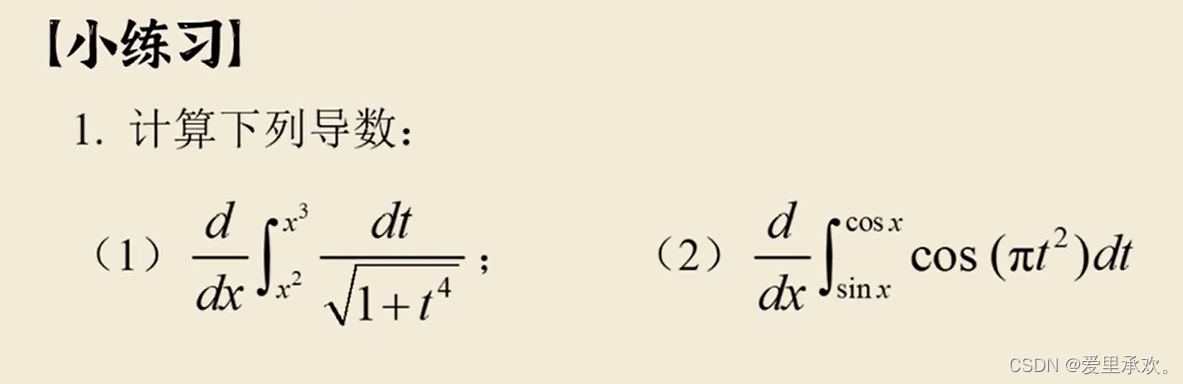

6.3、变限积分的“天然"连续性?


七、微积分基本定理?
7.1、牛顿 -- 莱布尼茨公式


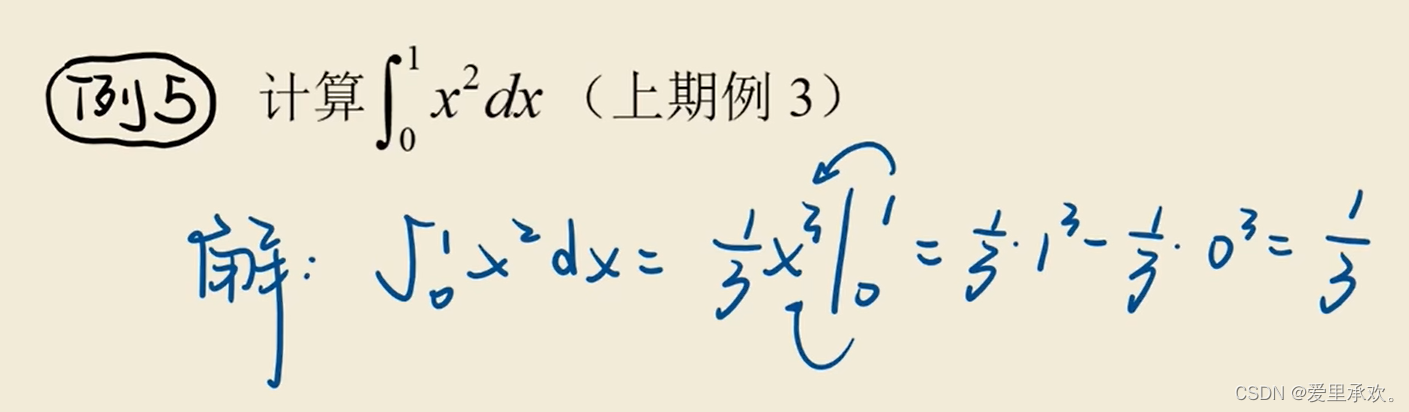

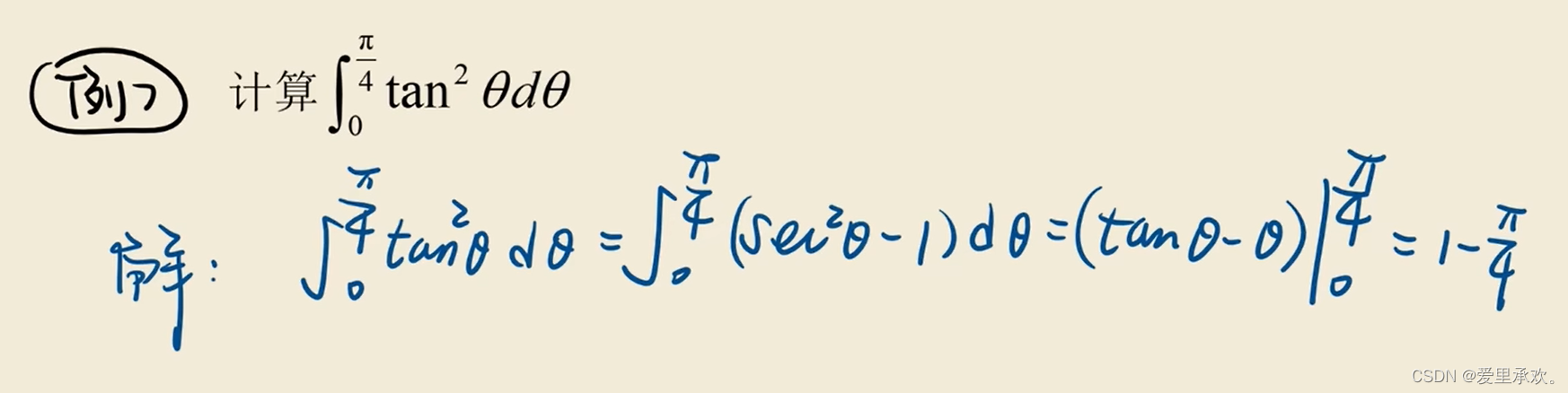
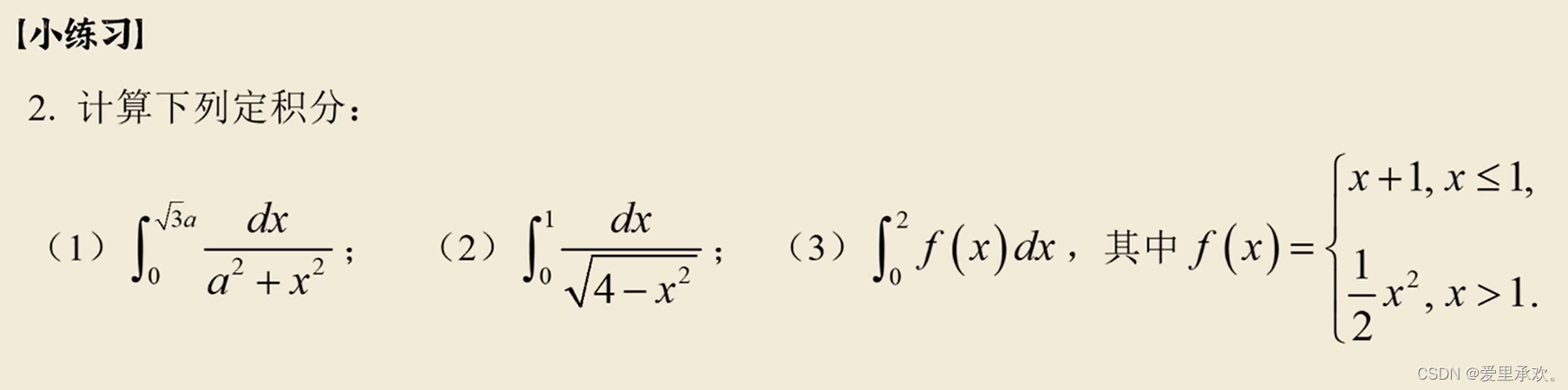


7.2、定积分基本方法?
7.2.1、换元法?

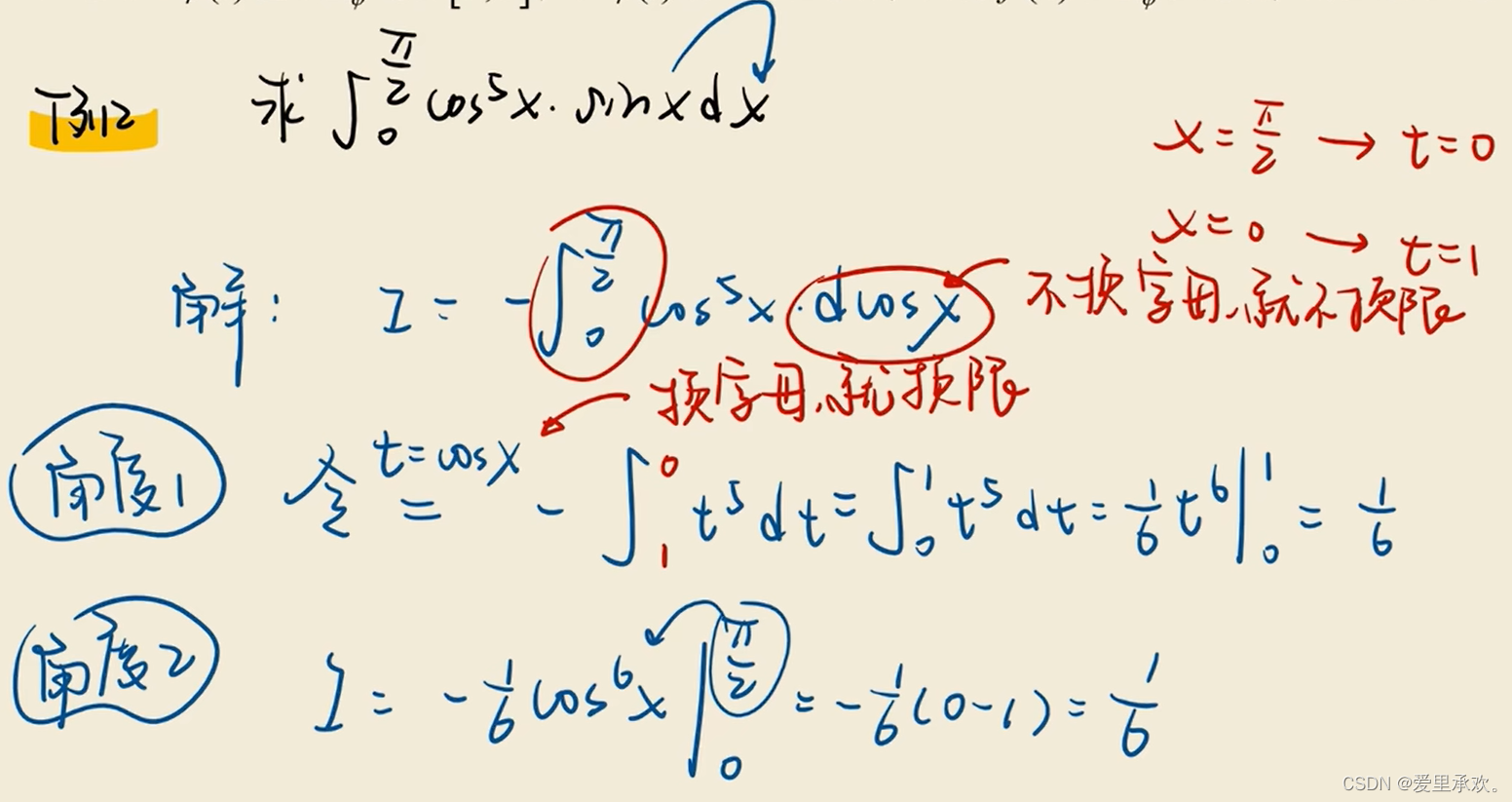
7.2.2、分部积分法?
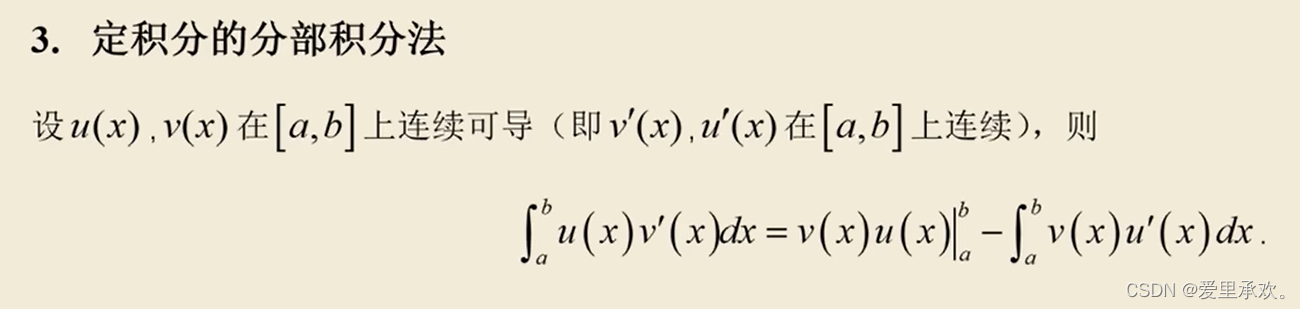
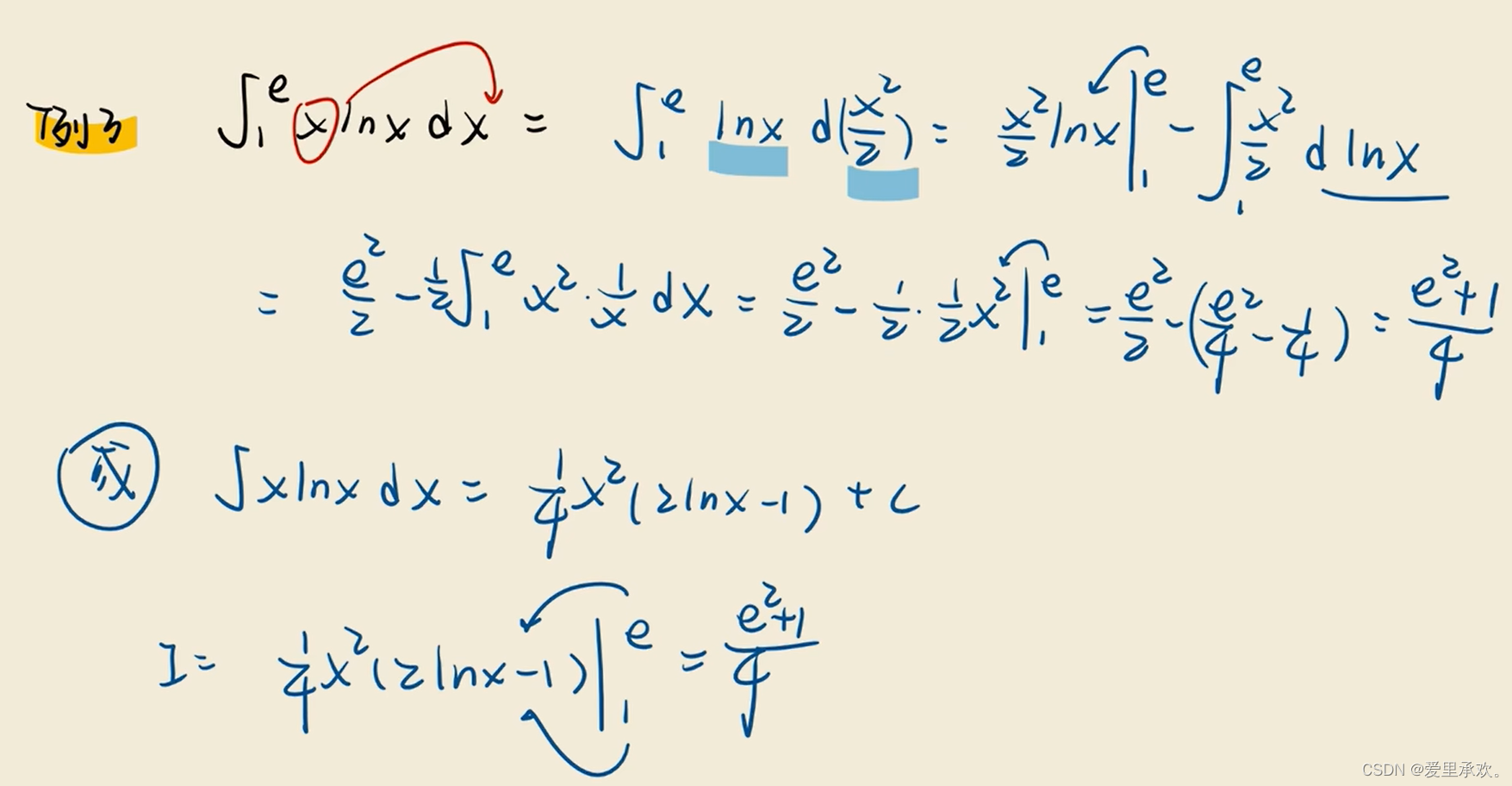



八、定积分 · 经典结论
8.1、对称区间


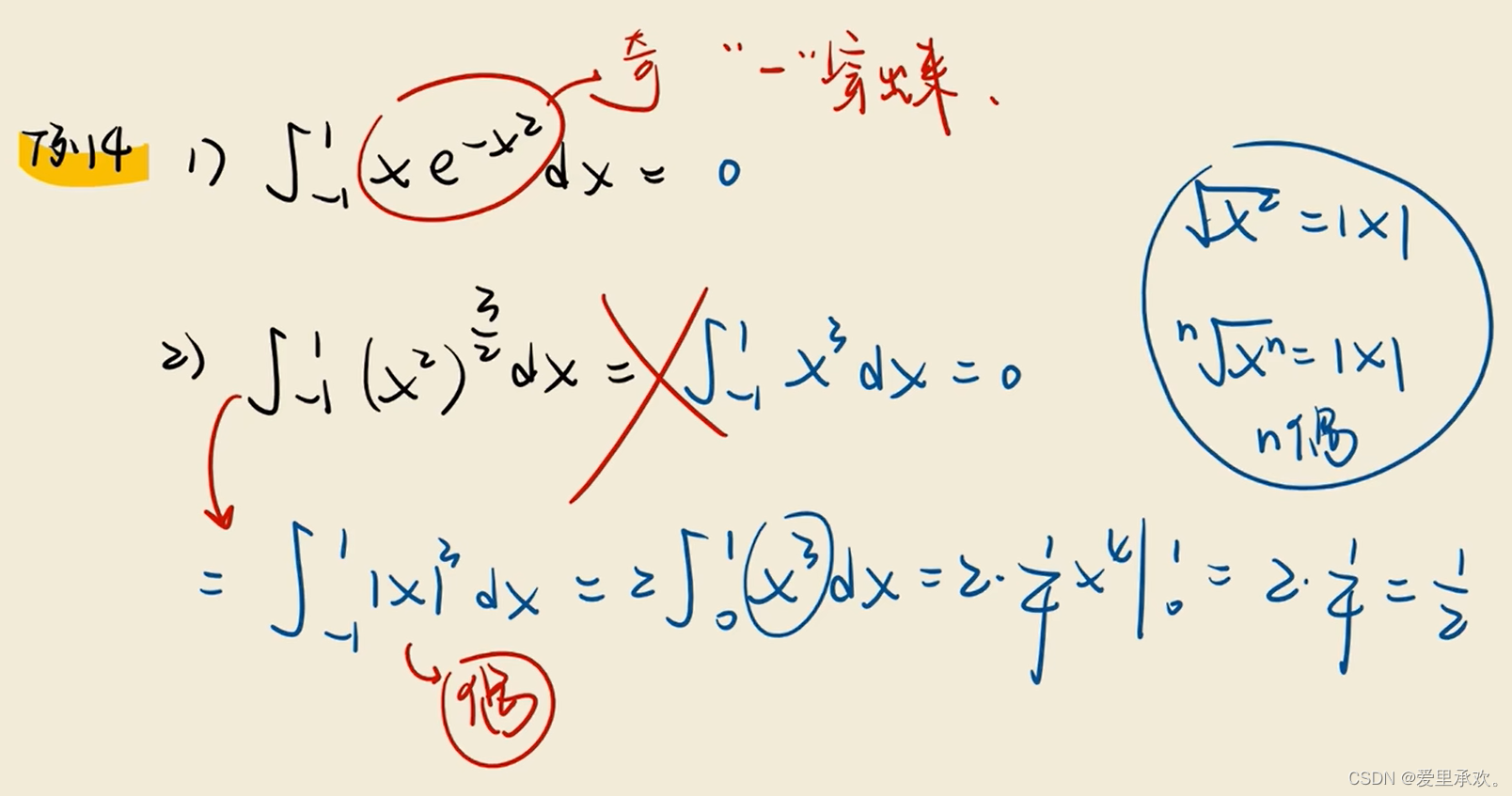
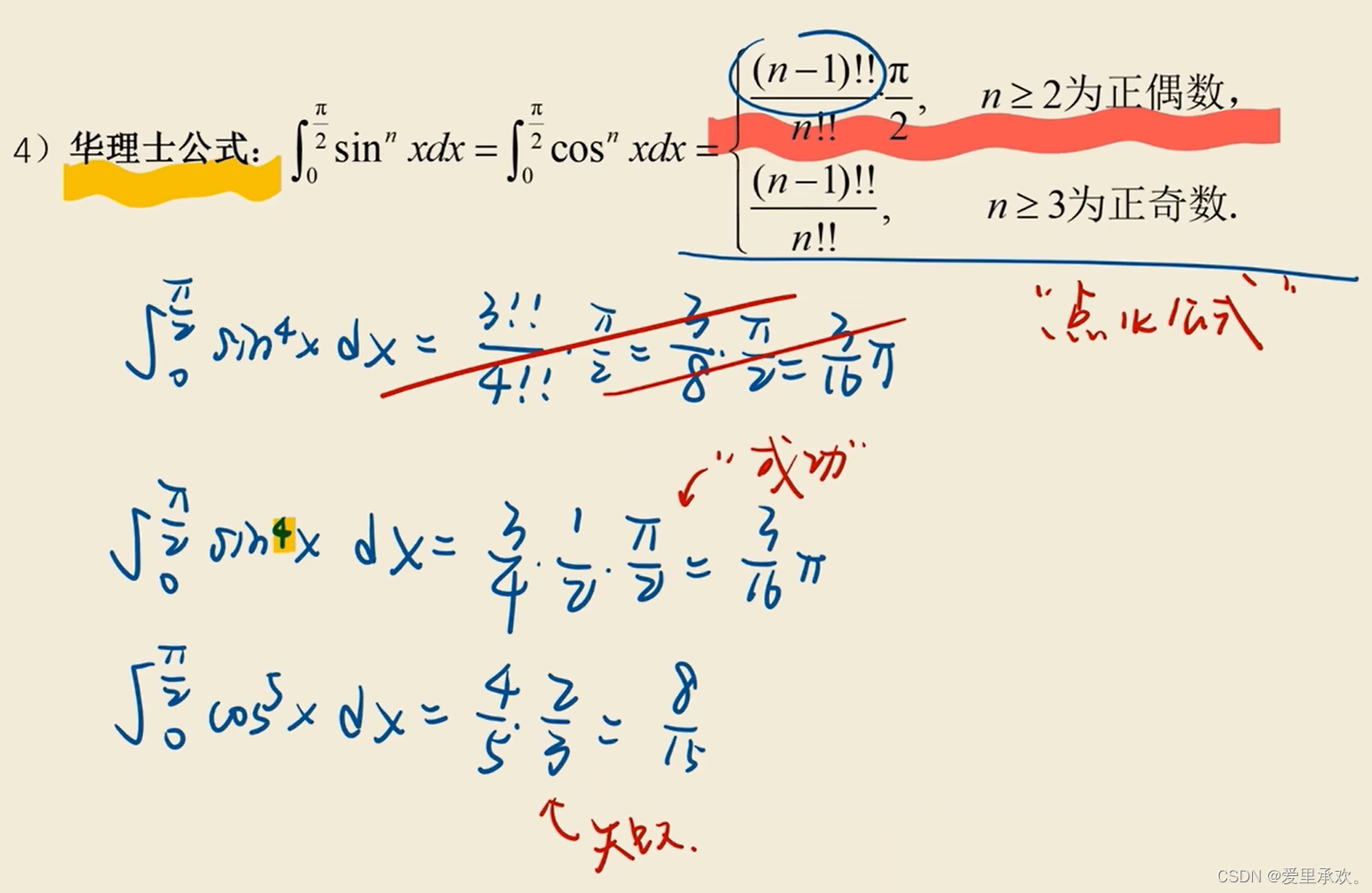
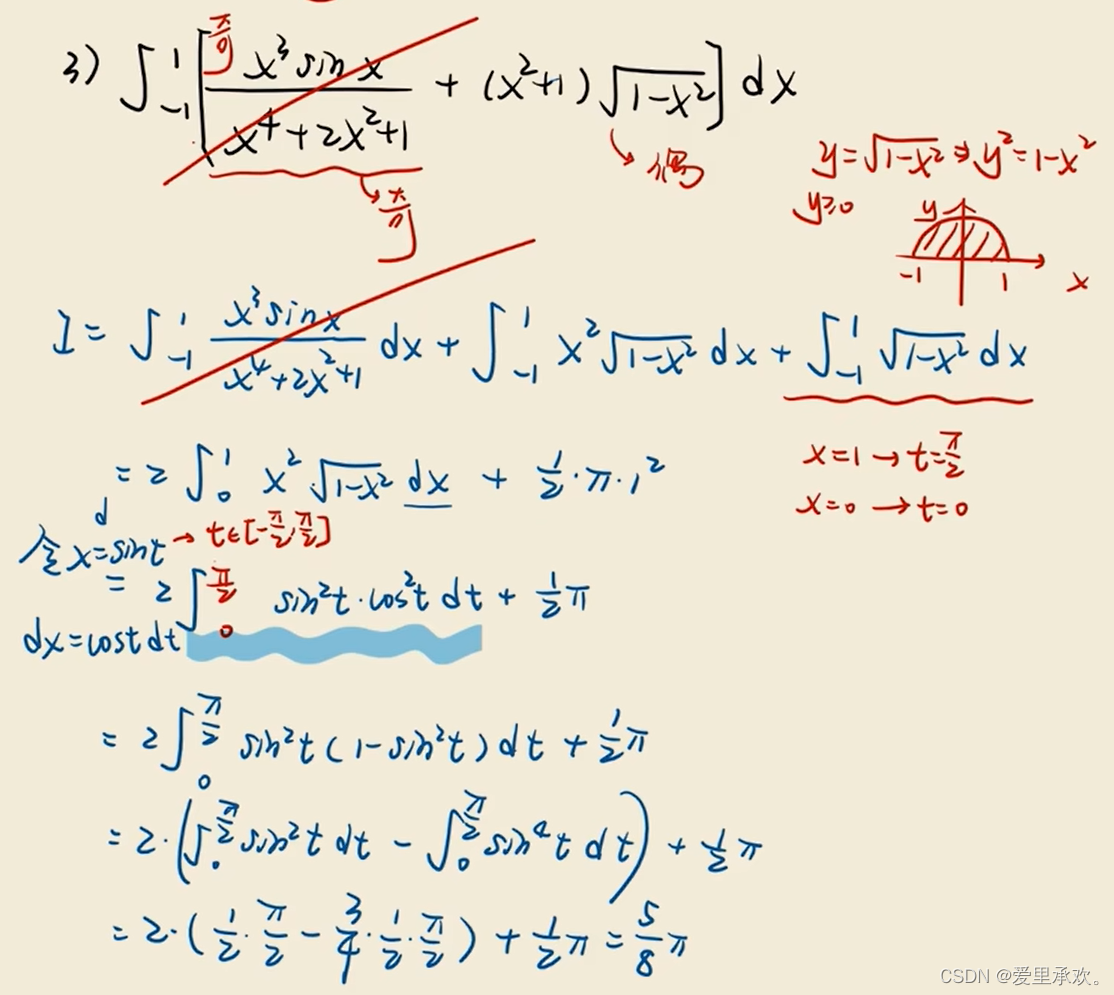


 8.2、区间再现公式
8.2、区间再现公式

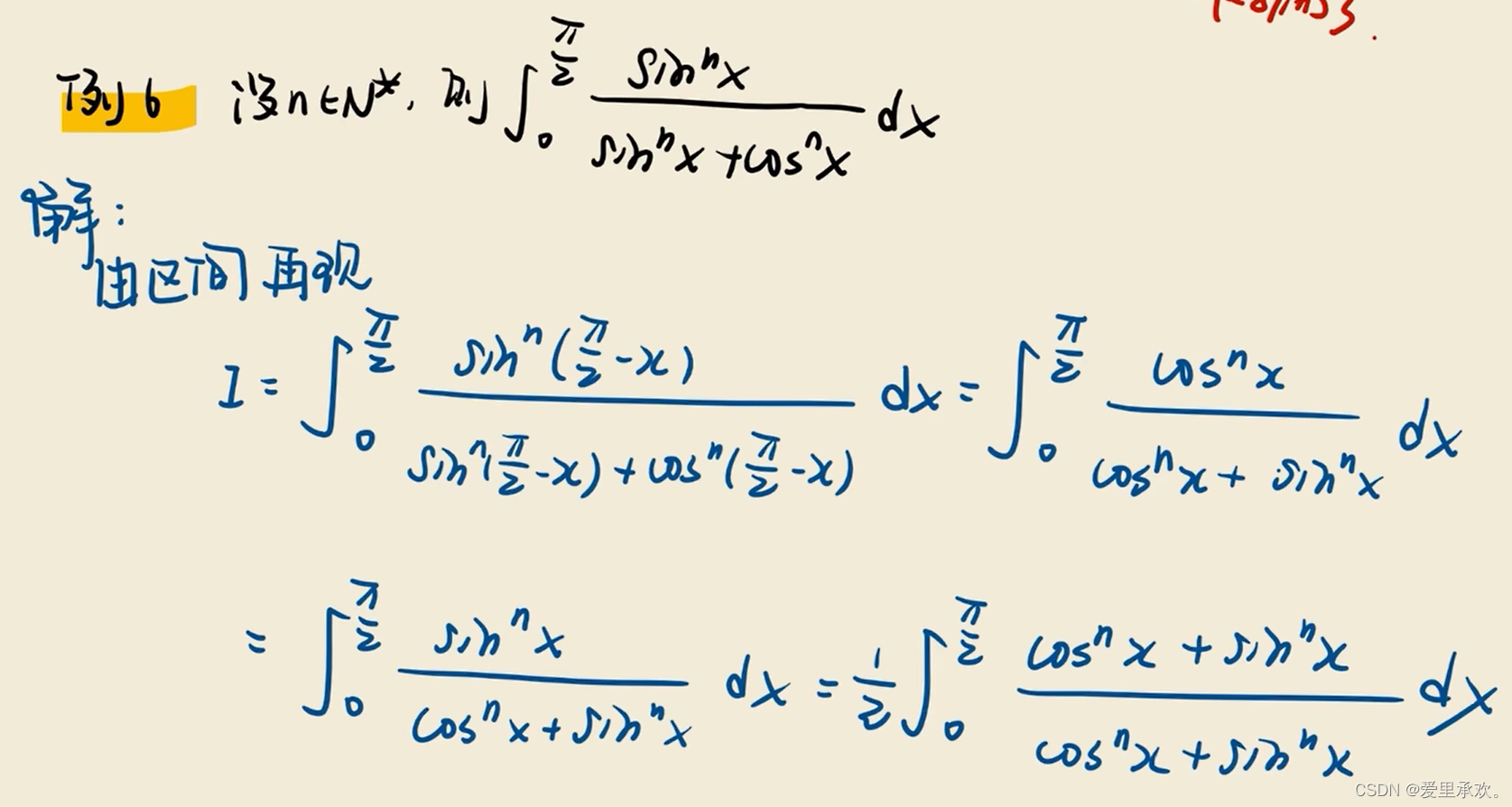
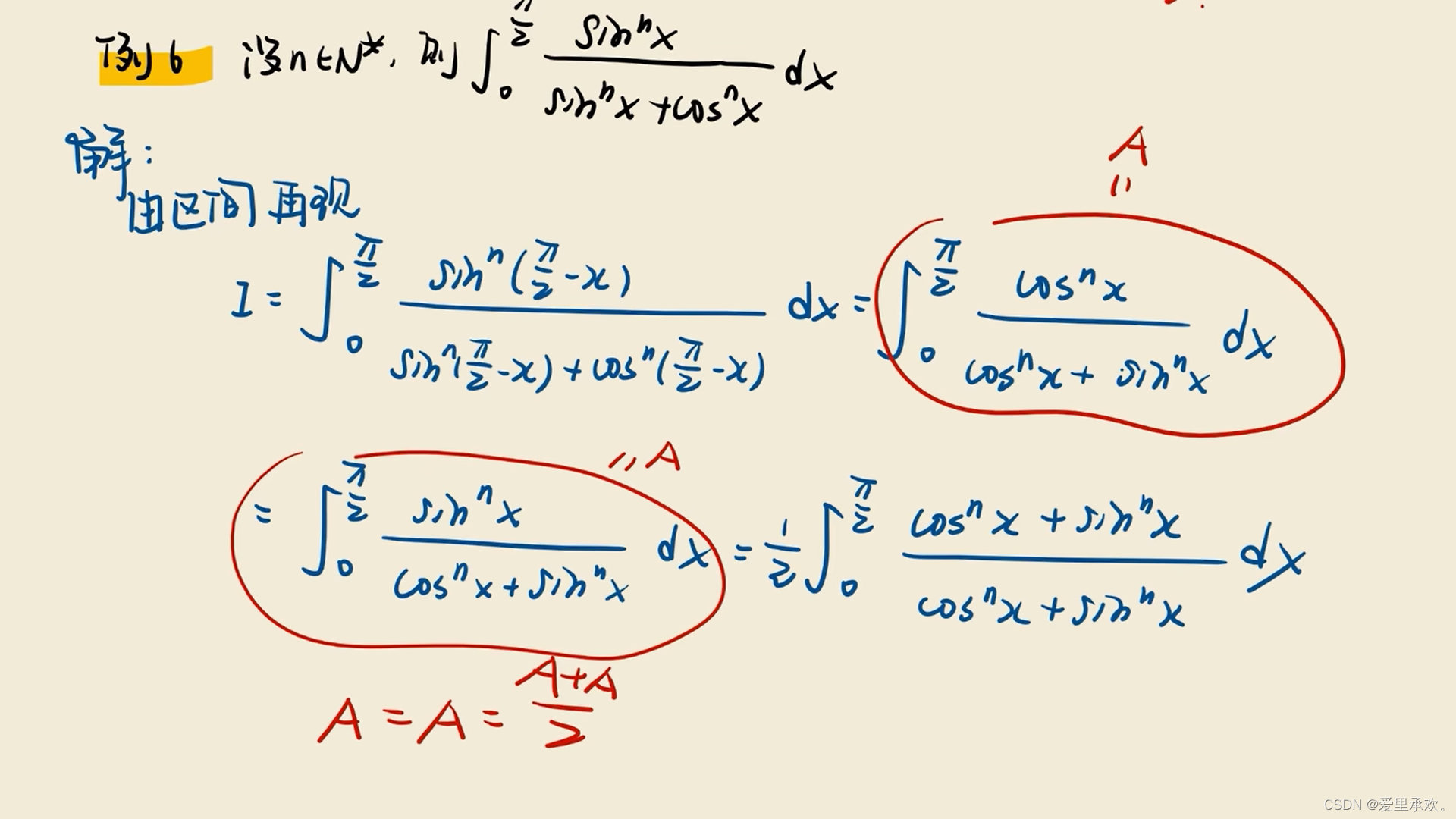
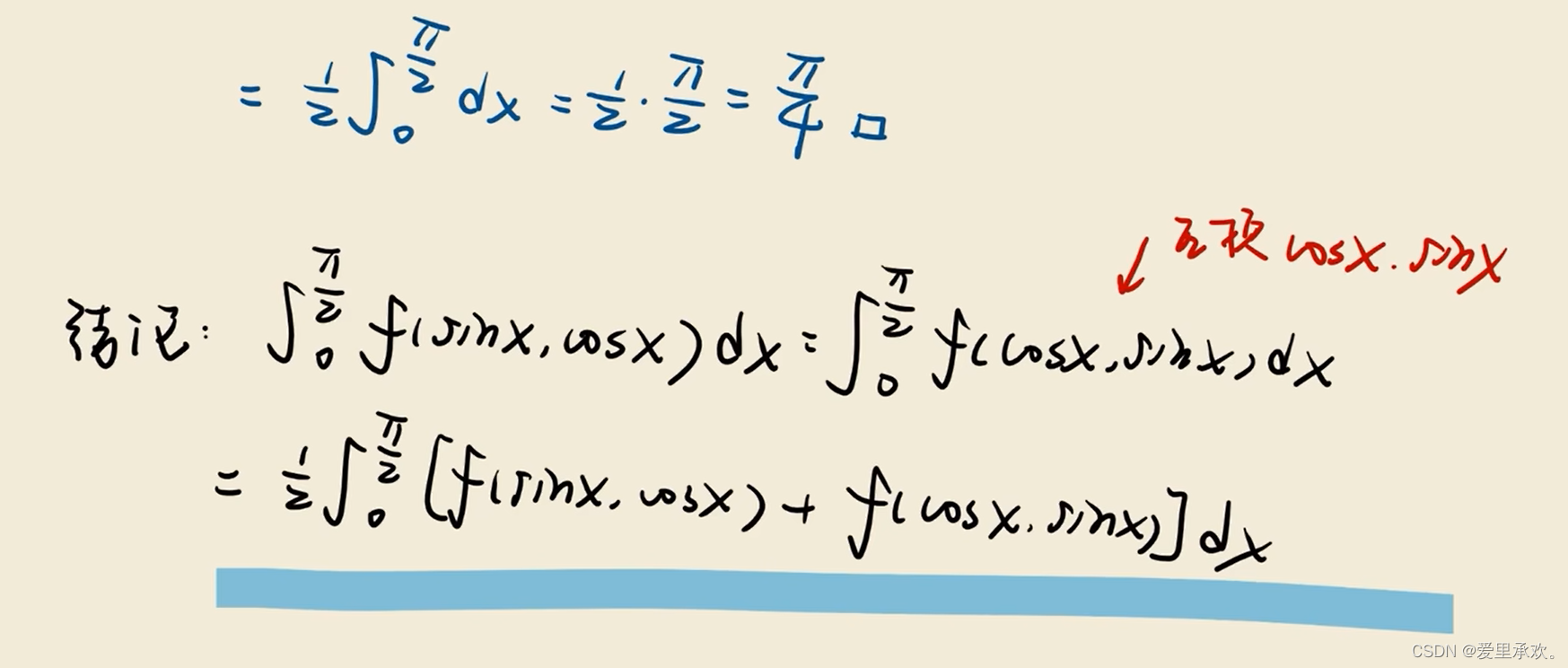

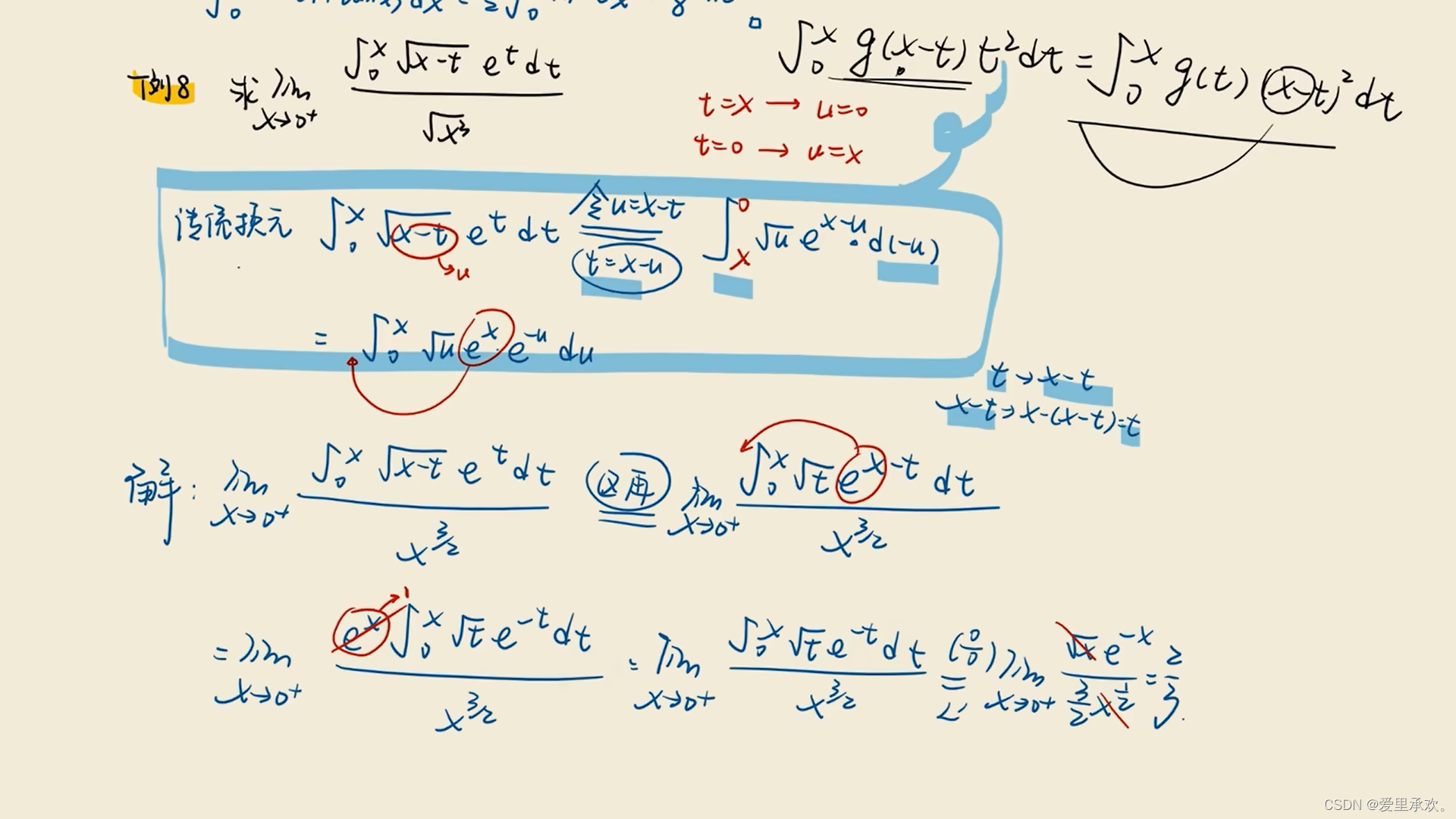 8.3、三角函数积分变换公式
8.3、三角函数积分变换公式

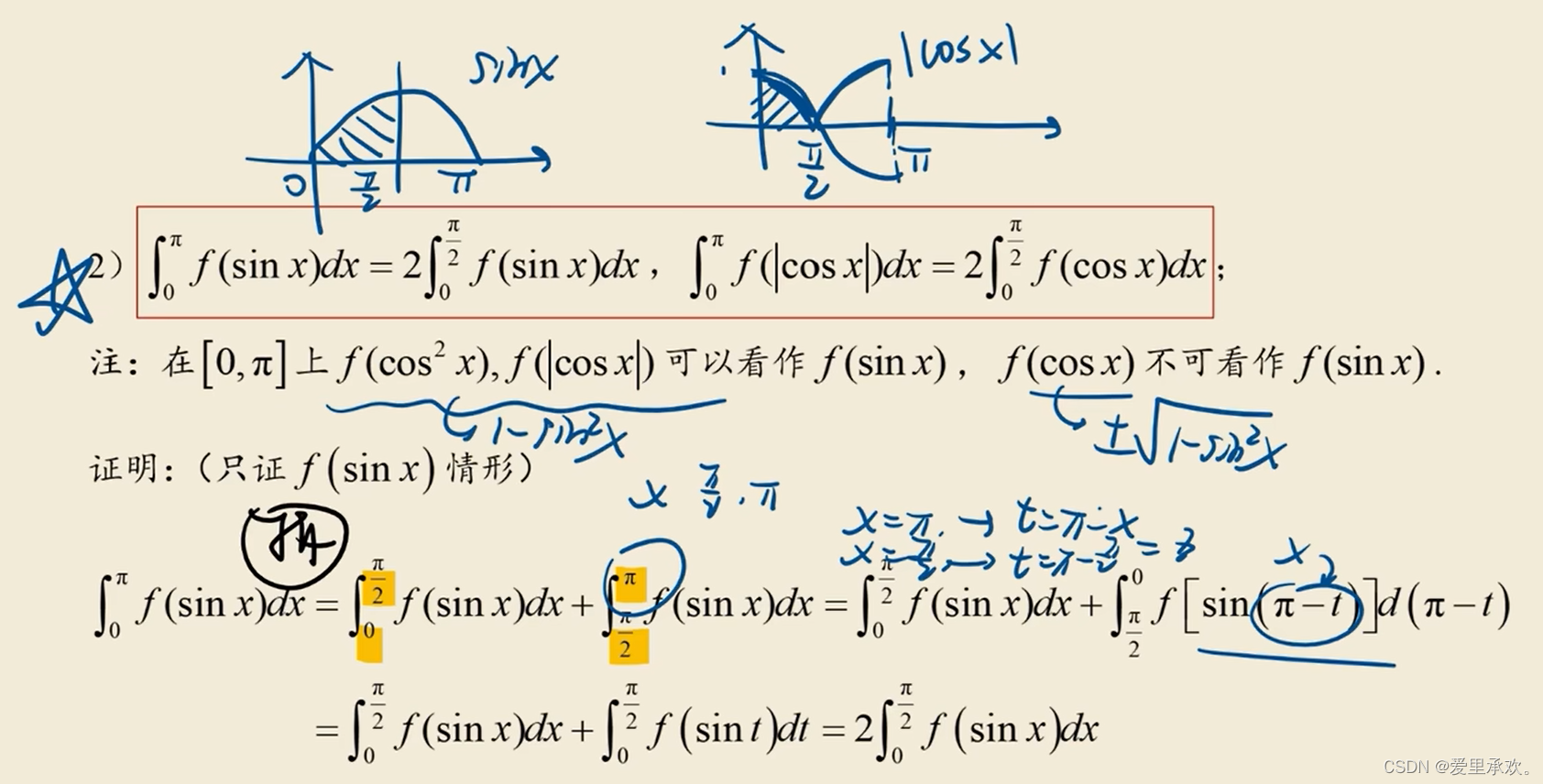
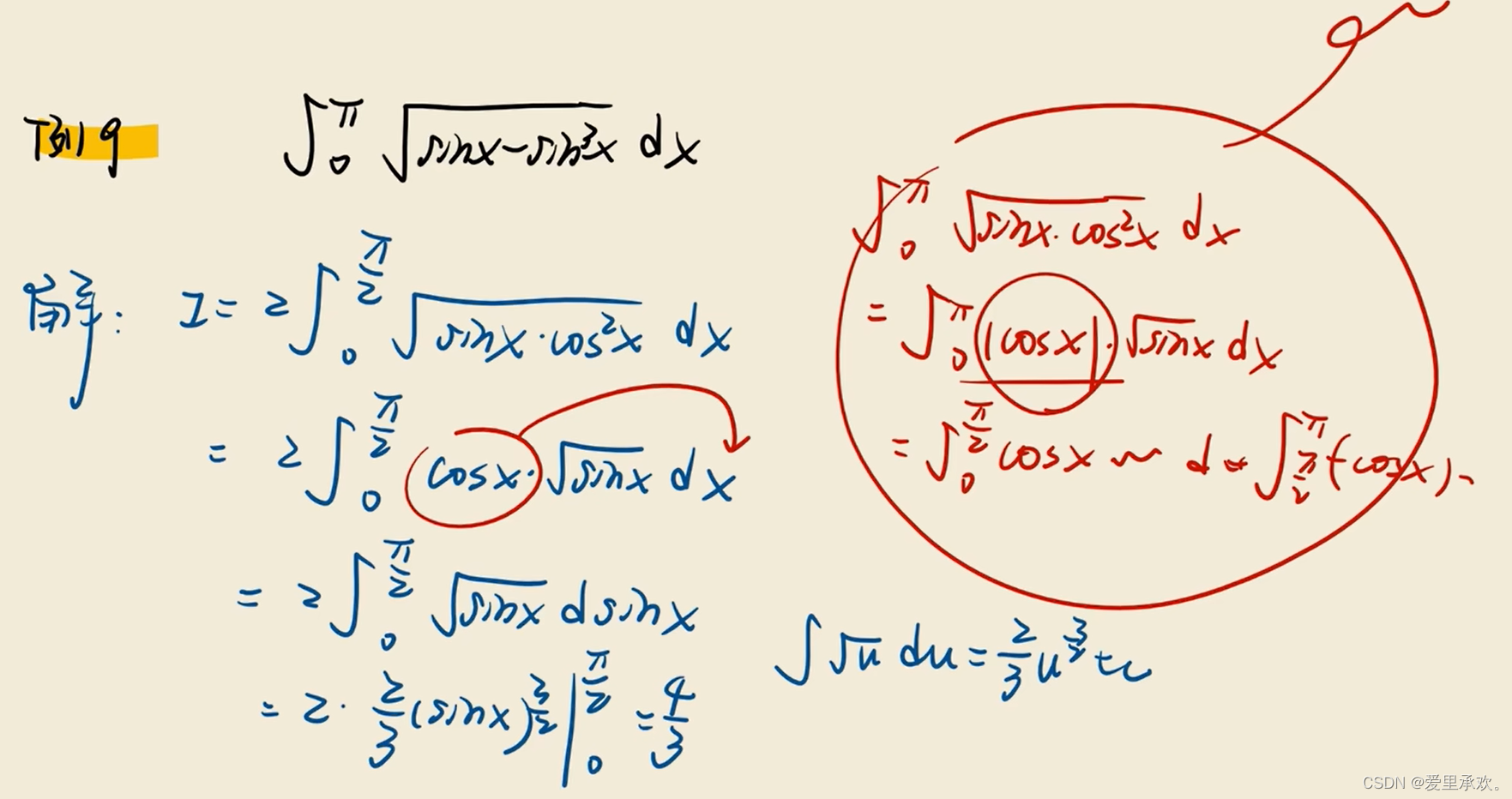
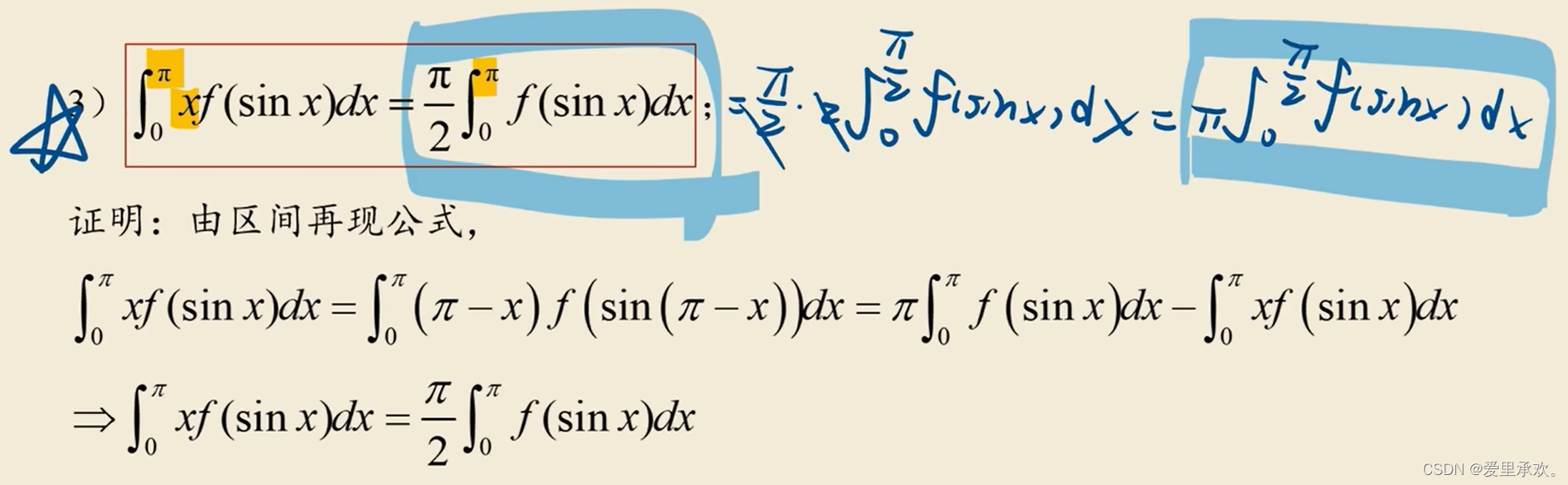
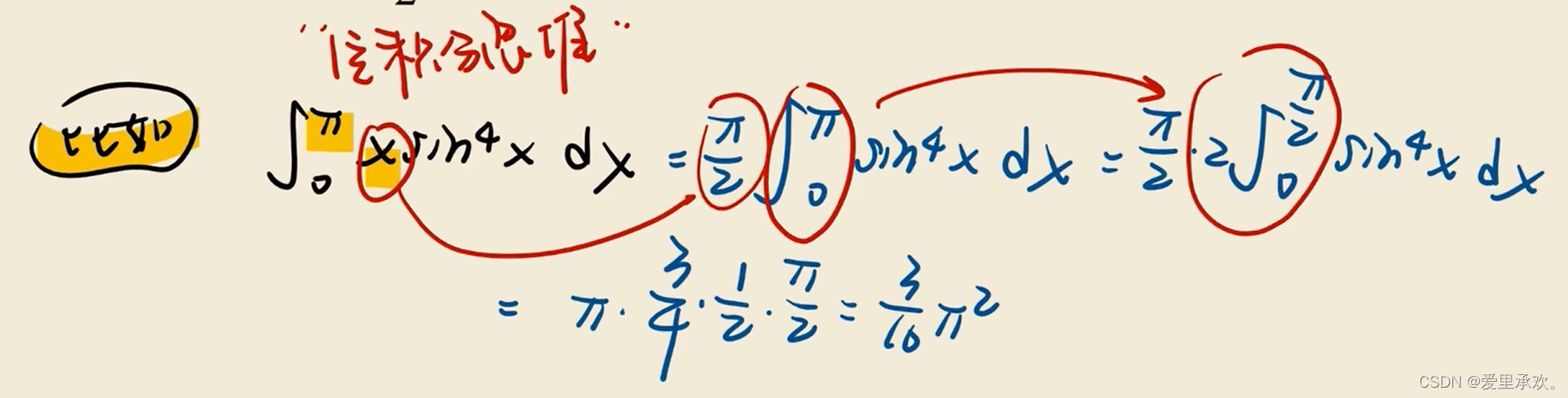
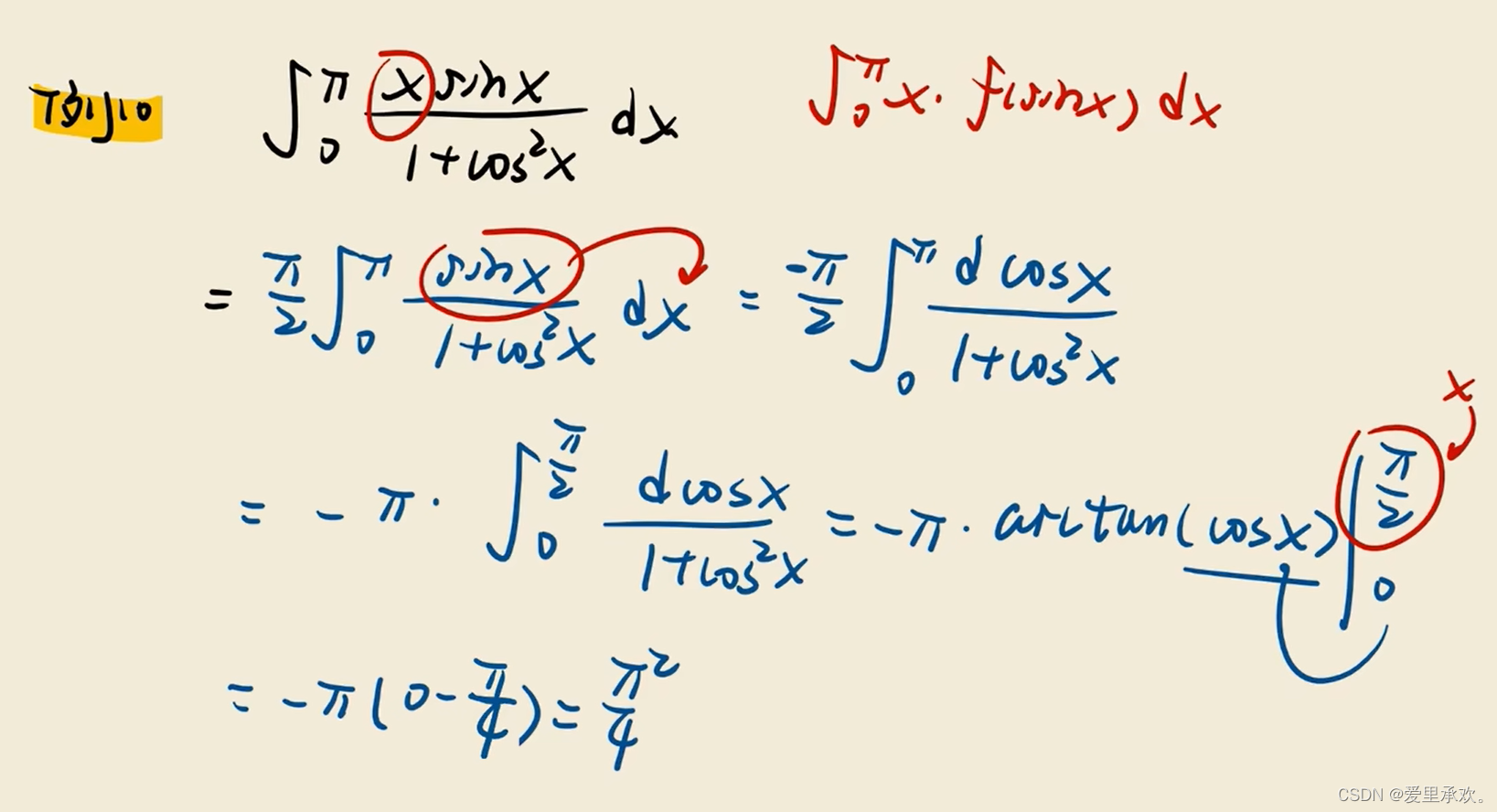

8.4、周期函数积分变换公式?


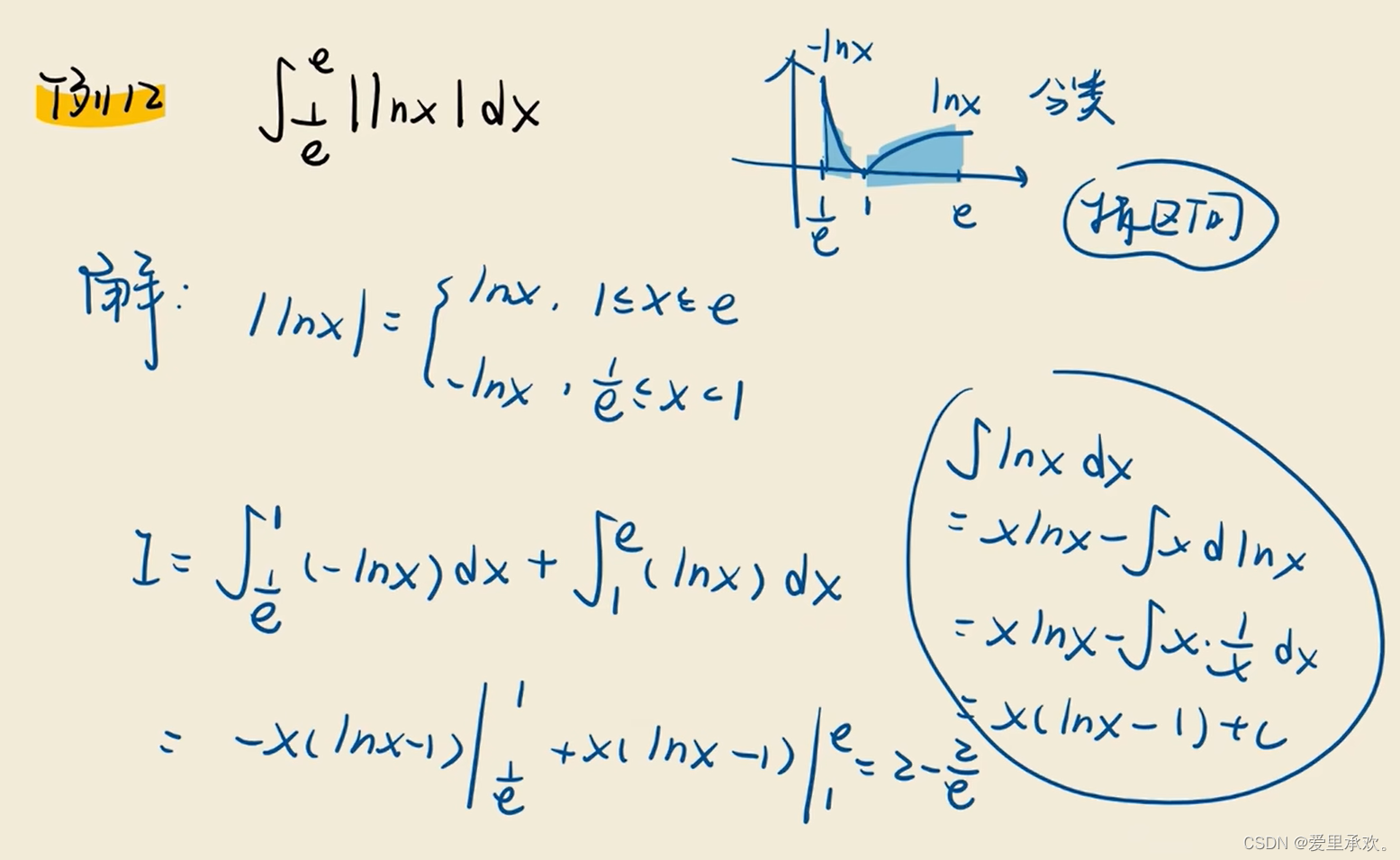

文章来源:https://blog.csdn.net/zhhdbehx/article/details/135593925
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
