Leetcoder Day5 | 哈希表理论基础 及 Part 1

语言：Java/C++?

目录

哈希表理论基础?

哈希表（Hash table）

哈希函数

拉链法

线性探测法

常见的三种哈希结构

242.有效的字母异位词?

349.?两个数组的交集?

集合法

数组法

202.?快乐数

1.?两数之和??

语法总结（Java）

今日心得

---

哈希表理论基础?

哈希表（Hash table）

1. 性质：根据关键码的值而直接进行访问的数据结构，数组就是一个哈希表，牺牲空间换时间
2. 作用：可用来快速判断一个元素是否出现集合里
3. 适用场景：当需要查询一个元素是否出现过，或者一个元素是否在集合里的时候，就要第一时间想到哈希法。

哈希函数

哈希函数通过hashCode把名字转化为数值，一般hashcode是通过特定编码方式，可以将其他数据格式转化为不同的数值。

问题：

1. 如果hashCode得到的数值大于哈希表的大小怎么办？为了保证映射出来的索引数值都落在哈希表上，会对数值做一个取模的操作，可以保证所有元素一定可以映射到哈希表上。
2. 如果元素的数量大于哈希表的大小怎么办？
   这便是哈希碰撞现象，有两种解决办法：线形探测法和拉链法

拉链法

如上图所示，小李和小王两个位置发生冲突，可以将发生冲突的元素都存储在链表中。 这样就可以通过索引找到小李和小王了。

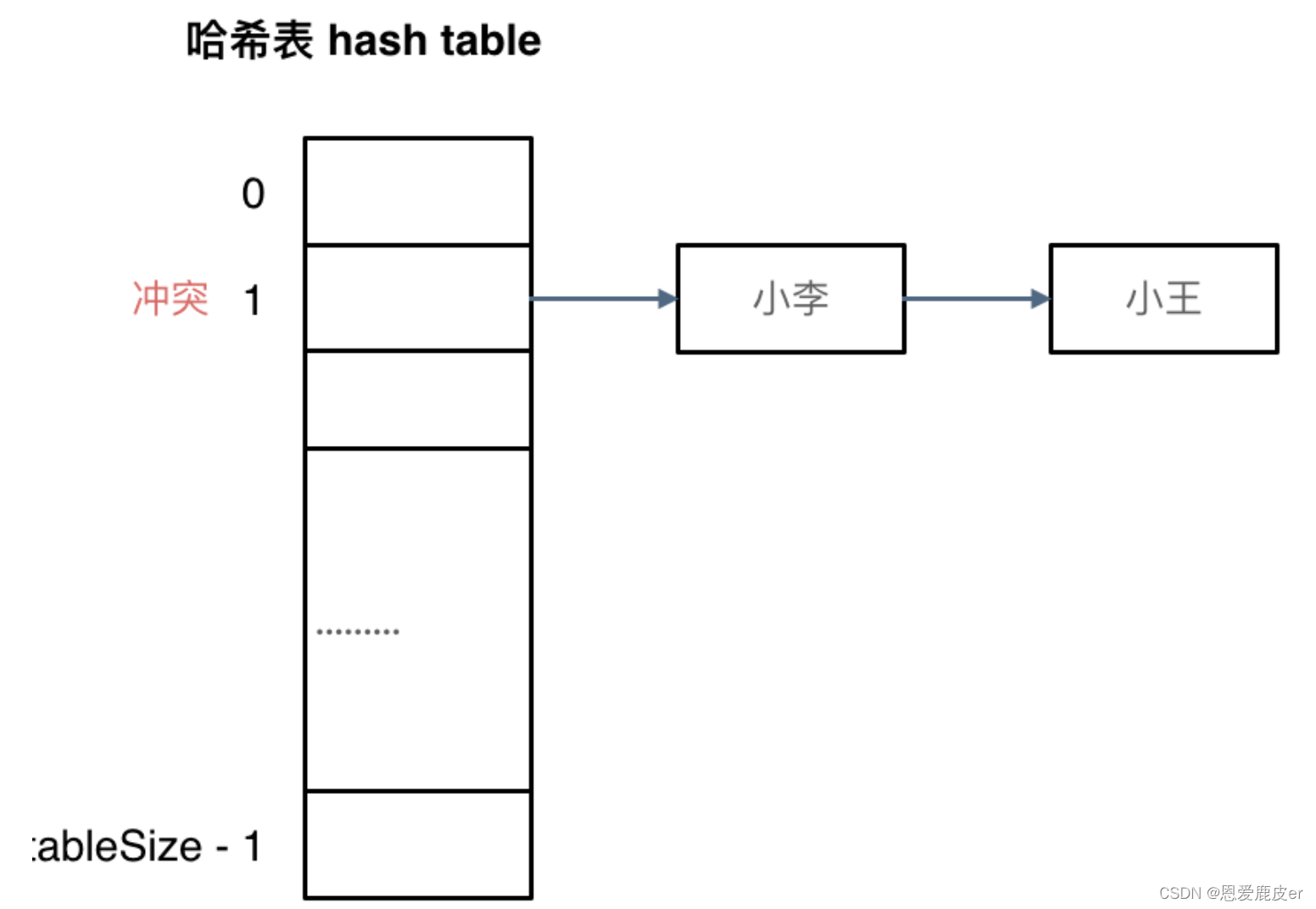
拉链法就是要选择适当的哈希表的大小，这样既不会因为数组空值而浪费大量内存，也不会因为链表太长而在查找上浪费太多时间。

线性探测法

这个方法中，一定要保证tableSize>dataSize，利用表中的空位来解决碰撞问题

如冲突的位置，放了小李，那么就向下找一个空位放置小王的信息。所以要求tableSize一定要大于dataSize ，要不然哈希表上就没有空置的位置来存放 冲突的数据了。

常见的三种哈希结构

• 数组
• set （集合）
• map(映射)

C++中的set 和 map 性质：

集合	底层实现	是否有序	数值是否可以重复	能否更改数值	查询效率	增删效率
std::set	红黑树	有序	否	否	O(log n)	O(log n)
std::multiset	红黑树	有序	是	否	O(logn)	O(logn)
std::unordered_set	哈希表	无序	否	否	O(1)	O(1)

红黑树是一种平衡二叉搜索树，所以key值是有序的，但key不可以修改，改动key值会导致整棵树的错乱，所以只能删除和增加。

使用集合来解决哈希问题的时候，如果需要不重复，优先使用unordered_set，因为它的查询和增删效率是最优的；如果需要集合是有序的，那么就用set，如果要求不仅有序还有重复数据的话，那么就用multiset。

对于Java版本，分为HashSet和TreeSet，因此使用HashSet来进行哈希操作。具体的有关于Java集合相关知识参考Java基础之Set_java set-CSDN博客?

映射	底层实现	是否有序	数值是否可以重复	能否更改数值	查询效率	增删效率
std::map	红黑树	key有序	key不可重复	key不可修改	O(logn)	O(logn)
std::multimap	红黑树	key有序	key可重复	key不可修改	O(log n)	O(log n)
std::unordered_map	哈希表	key无序	key不可重复	key不可修改	O(1)	O(1)

std::map 和std::multimap 的key也是有序的。

Java版本参考Java基础知识之Map_java map-CSDN博客

242.有效的字母异位词?

给定两个字符串 s 和 t ，编写一个函数来判断 t 是否是 s 的字母异位词。

示例?1: 输入: s = "anagram", t = "nagaram" 输出: true

示例 2: 输入: s = "rat", t = "car" 输出: false

说明:?你可以假设字符串只包含小写字母。

本题很容易想到的一个思路就是利用两次for循环，还要记录字符出现的次数，这个是暴力解法，因此空间和时间复杂度都比较大。

可以考虑哈希表因为哈希表可以直接判断是否存在某个元素，定义一个数组record，用来记录字符串s里字符出现的次数。字符a到字符z的ASCII是26个连续的数值，所以不用计算每个字符的ASCII数值，而是取和"a" 的位置差即可。遍历字符串s的时候，将record中位置为s[i]-'a'的元素的值+1即可，这样就将字符串s中字符出现的次数统计出来了。

随后遍历字符串t，若某个字符在record数组的值不为0，则将t中出现的字符映射哈希表索引上的数值再做-1的操作。最后如果record数组如果有的元素不为零0，说明字符串s和t一定是谁多了字符或者谁少了字符，return false。若record数组所有元素都为零0，说明字符串s和t是字母异位词，return true。

class Solution {
    public boolean isAnagram(String s, String t) {
        int[] record=new int[26];
        for(int i=0;i<s.length();i++){
            record[s.charAt(i)-'a']++;
        }
        for (int i = 0; i < t.length(); i++) {
            record[t.charAt(i) - 'a']--;
        }
        for(int count:record){
            if (count!=0){
                return false;
            }
        }
        return true;
    }
}

???使用数组来做哈希的题目，是因为题目都限制了数值的大小。如果哈希值比较少、特别分散、跨度非常大，使用数组就造成空间的极大浪费。

349.?两个数组的交集?

给定两个数组，编写一个函数来计算它们的交集

输出结果中的每个元素一定是唯一的。 我们可以不考虑输出结果的顺序。

示例 1：

输入：nums1 = [1,2,2,1], nums2 = [2,2]
输出：[2]

示例 2：

输入：nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出：[9,4]
解释：[4,9] 也是可通过的

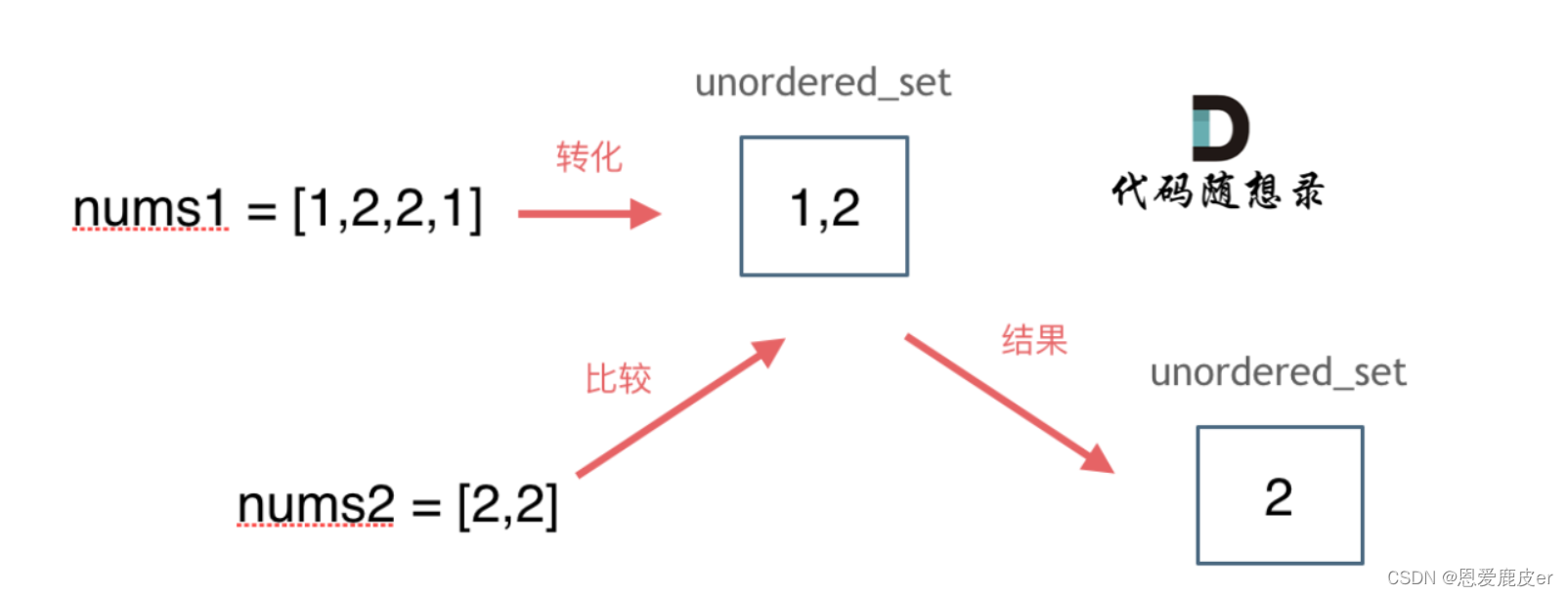
集合法

在理论基础中有总结，C++中关于集合有std::set，std::multiset，std::unordered_set三种结构，其中unordered_set底层实现是哈希表且是官方认证版本，读写效率是最高的。而且不需要对数据进行排序，而且还不让数据重复，适合本题的设置，因此使用unordered_set。

class Solution {
public:
    vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
        unordered_set<int> result;  //给结果集去重
        unordered_set<int> nums_set(nums1.begin(), nums1.end());
        for(int i=0; i<nums2.size();i++){
            if(nums_set.find(nums2[i])!=nums_set.end()){
                result.insert(nums2[i]);
            }
        }
        return vector<int>(result.begin(),result.end());

    }
};

Java

import java.util.Set;
import java.util.HashSet;

class Solution {
    public int[] intersection(int[] nums1, int[] nums2) {
        if(nums1==null||nums1.length==0||nums2==null||nums2.length==0){
            return new int[0];
        }
        Set<Integer> num_set=new HashSet<>();
        Set<Integer> result=new HashSet<>();

        //将nums1存入num_set中
        for(int i:nums1){
            num_set.add(i);
        }
        //遍历nums2看是否存在nums1的交集
        for(int i:nums2){
            if(num_set.contains(i)){
                result.add(i);
            }
        }
        return result.stream().mapToInt(x->x).toArray();
    }
}

• 时间复杂度: O(n + m) m 是最后要把 set转成vector
• 空间复杂度: O(n)

数组法

本题后来Leetcode修改了题设，把范围设置在了：

• 1 <= nums1.length, nums2.length <= 1000
• 0 <= nums1[i], nums2[i] <= 1000

class Solution {
    public int[] intersection(int[] nums1, int[] nums2) {
       int[] hash=new int[1001];
       List<Integer> result=new ArrayList<>();
       for(int i:nums1){
           hash[i]=1;
       }
       for(int i:nums2){
           if(hash[i]==1){
               result.add(i);
               hash[i]=-1;  //防止重复的元素也被添加到result里
           }
       }
       int idx=0;
       int res[]=new int[result.size()];
       for(int i:result){
           res[idx++]=i;
       }
       return res;
    }
}

---

202.?快乐数

编写一个算法来判断一个数 n 是不是快乐数。

「快乐数」定义为：对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和，然后重复这个过程直到这个数变为 1，也可能是无限循环但始终变不到 1。如果 可以变为? 1，那么这个数就是快乐数。

如果 n 是快乐数就返回 True ；不是，则返回 False 。

示例：

输入：19
输出：true
解释：
1^2 + 9^2 = 82
8^2 + 2^2 = 68
6^2 + 8^2 = 100
1^2 + 0^2 + 0^2 = 1

1 <= n <= 231 - 1

本题看着好像很复杂，但实际上可以分步思考，首先第一步就是先进行各个位置上的求和操作，这个是一个基本题了，思路就是：

将数字取余，即当前最低位所对应的数字，求平方和，随后除10取整数再次进入循环，直到所有位置上都进行了平方和并都加在一起为止。

随后需要进行的就行判断是否为快乐数的工作，建立一个unordered_set进行存储，若当前的sum==1，说明是快乐数，返回true，若sum不等于1且没有出现在过unordered_set中存储进unordered_set，再次对新的sum进行各个位数和计算。若计算了n轮后sum不等于1且出现在当中，说明是一个是无限循环的数，返回false。

import java.util.Set;
import java.util.HashSet;

class Solution {
    public int getSum(int n) {
        int sum=0;
        while(n>0){
            int temp=n%10;
            sum+= temp*temp;
            n/=10;
        }
        return sum;
    }

    public boolean isHappy(int n) {
        Set<Integer> record= new HashSet<>();
        while(true){
            int sum=getSum(n);
            if(sum==1) {return true;}
            if(record.contains(sum)){
                return false;
            }
            else{
                record.add(sum);
            }
            n=sum;
        }
        

    }
}

---

1.?两数之和??

给定一个整数数组?nums?和一个整数目标值?target，请你在该数组中找出和为目标值?target的那两个?整数，并返回它们的数组下标。

你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。

你可以按任意顺序返回答案。

示例 1：

输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。

示例 2：

输入：nums = [3,2,4], target = 6
输出：[1,2]

示例 3：

输入：nums = [3,3], target = 6
输出：[0,1]

暴力解法同样需要用两层for循环来进行查找，时间复杂度为O(N^2)，因此使用哈希表可以将寻找的时间复杂度降低到 O(N)。

本题不仅要判断元素是否存在而且还要记录元素的下标位置，需要采用一种key-value结构来存放，那么使用map正合适。回顾哈希表理论基础中的表格，本题不要求列表有序，但是要求不重复，选择std::unordered_map 效率更高。下面进一步思考：

• map用来做什么：存放访问过的元素
• map中key和value分别表示什么：因为需要判断元素是否出现，这个元素就要作为key，key对应的就是value，所以value存放下标。

接下来的思路就是，当我们遇到nums[i]，求target-nums[i]的值，在map中寻找是否存在key等于这个值的元素，若没有，将这个元素存储在map中继续寻找。若找到，则返回当前元素和找到的这个元素在map中对应的value值，因此是按照从左往右存储的，所以找到的target-nums[i]在是第一个位置，当前的元素在第二个位置。

class Solution {
    public int[] twoSum(int[] nums, int target) {
        int[] record=new int[2];
        if(nums.length==0||nums==null){
            return record;
        }
        Map <Integer, Integer> map= new HashMap<>();
        for(int i=0;i<nums.length;i++){
            int temp=target-nums[i];
            if(map.containsKey(temp)){//若res存在于map中
                record[1]=i; //结果中的第二个值为当前元素对应的键值，即下标
                record[0]=map.get(temp);//res值对应的下标存储在结果中的第一个位置
                break;
            }
        map.put(nums[i],i); //nums[i]对应key，i对应value
        }
    return record;
    }
}

---

语法总结（Java）

Set<Integer> num_set=new HashSet<>();   //创建新的整数集合
num_set.add(i);  //在集合里添加元素
num_set.contains(i) //判断集合里是否包含某元素
if(nums_set.find(i)!=nums_set.end()){}// 判断i的值是否出现在nums_set中，括号里为出现的情况
result.stream().mapToInt(x->x).toArray(); //将集合转换为数组


int[] hash=new int[n]; //创建大小为n的数组

List<Integer> result=new ArrayList<>(); //创建新的整数列表
result.add(i);  //在列表中添加元素


Map <Integer, Integer> map= new HashMap<>();   //创建二维映射<key，value>
map.containsKey(temp);  //判断映射中是否存在key=temp的元素
record[0]=map.get(temp);// 获取key=temp元素的value
map.put(nums[i],i); //nums[i]对应key，I对应value //将某元素的值和下标存在map中

今日心得

当遇到给定一组元素，判断某个元素是否出现过时，最适合用哈希表来解决。

数组🆚集合🆚映射：

在有限的情况下，也可以采用数组的方式，这里总结一下使用数组和集合的区别：

• 数组的大小是受限制的，如果哈希值比较少、特别分散、跨度非常大，使用数组就造成空间的极大浪费。
• set是一个集合，里面放的元素只能是一个key；使用set 占用空间比数组大，而且速度要比数组慢，set把数值映射到key上都要做hash计算的。

因此若遇到范围有限且不是分散的情况下，优先考虑数组，若没有限制数值的大小，可以优先考虑集合；若涉及到key-value结构，必用映射。