面试算法100:三角形中最小路径之和
发布时间:2024年01月08日
题目
在一个由数字组成的三角形中,第1行有1个数字,第2行有2个数字,以此类推,第n行有n个数字。例如,下图是一个包含4行数字的三角形。如果每步只能前往下一行中相邻的数字,请计算从三角形顶部到底部的路径经过的数字之和的最小值。从三角形顶部到底部的路径数字之和的最小值为11,对应的路径经过的数字用阴影表示。
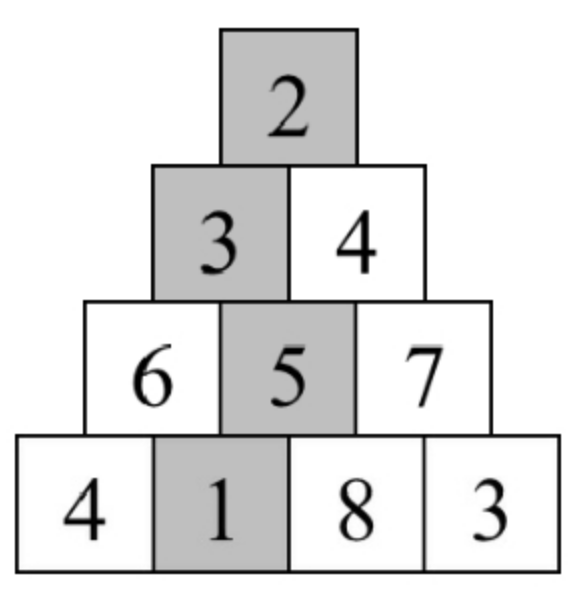
说明:从三角形顶部到底部的路径数字之和的最小值为11,对应的路径经过的数字用阴影表示
分析
可以移动三角形每行的位置使它们左端对齐
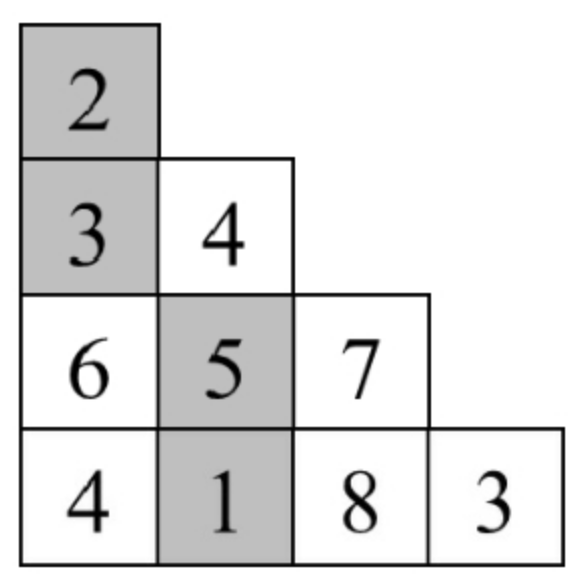
可以用f(i,j)表示从三角形的顶部出发到达行号和列号分别为i和j(i≥j)的位置时路径数字之和的最小值,同时用T[i][j]表示三角形行号和列号分别为i和j的数字。如果三角形中包含n行数字,那么f(n-1,j)的最小值就是整个问题的最优解。
解
public class Test {
public static void main(String[] args) {
List<Integer> list1 = Arrays.asList(2);
List<Integer> list2 = Arrays.asList(3, 4);
List<Integer> list3 = Arrays.asList(6, 5, 7);
List<Integer> list4 = Arrays.asList(4, 1, 8, 3);
List<List<Integer>> triangle = Arrays.asList(list1, list2, list3, list4);
int result = minimumTotal(triangle);
System.out.println(result);
}
public static int minimumTotal(List<List<Integer>> triangle) {
int size = triangle.size();
int[][] dp = new int[size][size];
for (int i = 0; i < size; i++) {
for (int j = 0; j <= i; j++) {
dp[i][j] = triangle.get(i).get(j);
if (i > 0 && j == 0) {// 最左边
dp[i][j] += dp[i - 1][j];
}
else if (i > 0 && i == j) {// 最右边
dp[i][j] += dp[i - 1][j - 1];
}
else if (i > 0) {
dp[i][j] += Math.min(dp[i - 1][j], dp[i - 1][j - 1]);
}
}
}
int min = Integer.MAX_VALUE;
for (int num : dp[size - 1]) {// 答案在最底层,选出一个最小的
min = Math.min(min, num);
}
return min;
}
}
文章来源:https://blog.csdn.net/GoGleTech/article/details/135459810
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- STM32(Cortex-M) 双堆栈MSP/PSP科普
- loki grpc_client
- 骨传导耳机排行榜前十名,骨传导耳机排行榜哪个牌子好?
- 关于js中ProgressEvent的属性
- 小狐狸GPT付费2.4.9 去除授权弹窗版
- Pytest测试中的临时目录与文件管理!
- HTML5 article标签,<time>...</time>标签和pubdate属性的运用
- leetcode刷题日志-383赎金信
- 饮用水除硝酸盐的方法
- MySQL主从复制与读写分离