归并算法排序

目录

归并排序

逆序对的数量

---

归并排序

题目如下：

给定你一个长度为?n?的整数数列。

请你使用归并排序对这个数列按照从小到大进行排序。

并将排好序的数列按顺序输出。

输入格式：

????????输入共两行，第一行包含整数?n。

????????第二行包含?n?个整数（所有整数均在?1～1091～109?范围内），表示整个数列。

输出格式：

????????输出共一行，包含?n?个整数，表示排好序的数列。

数据范围：1≤n≤100000

输入样例：

5
3 1 2 4 5

输出样例：

1 2 3 4 5

这道题目还是让我们排序,只不过这里强制要求我们使用归并排序,所以既然如此的话,让我们好好地康康这道题目

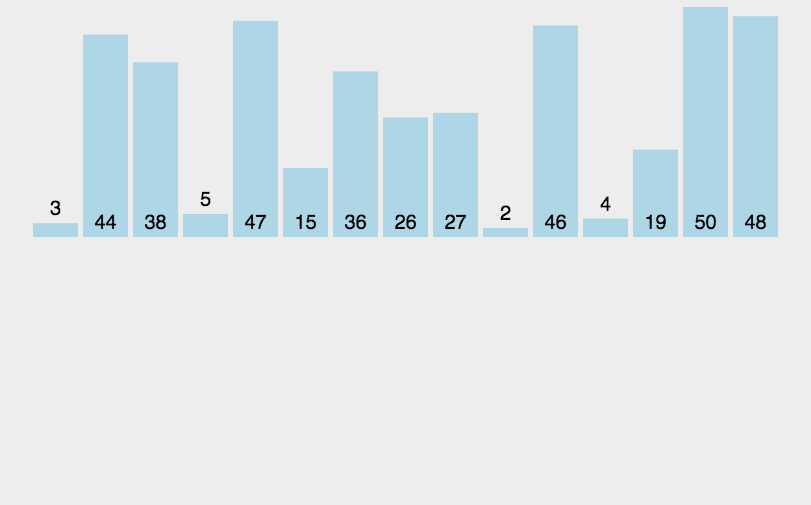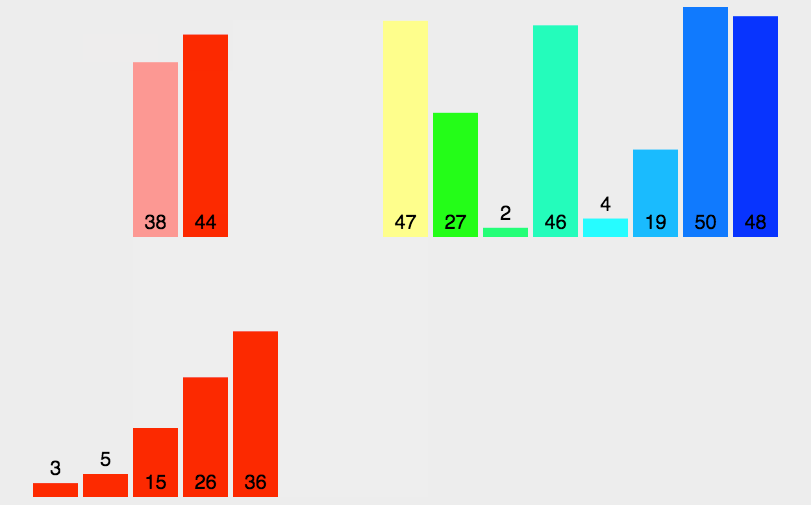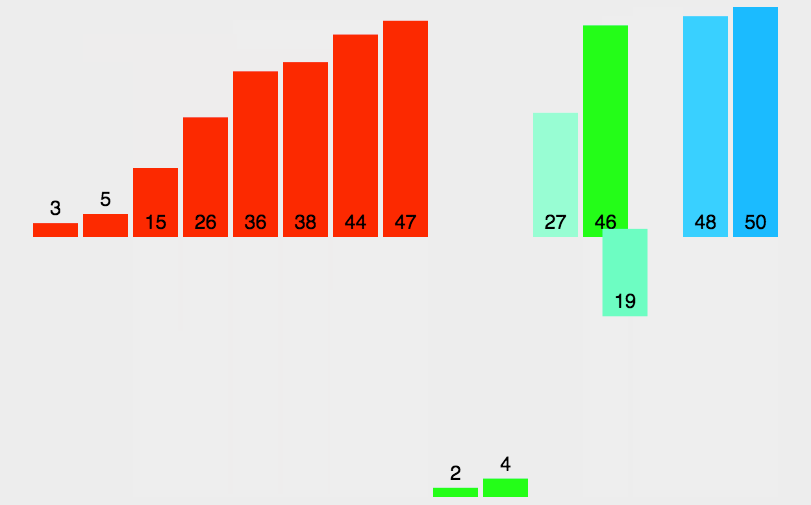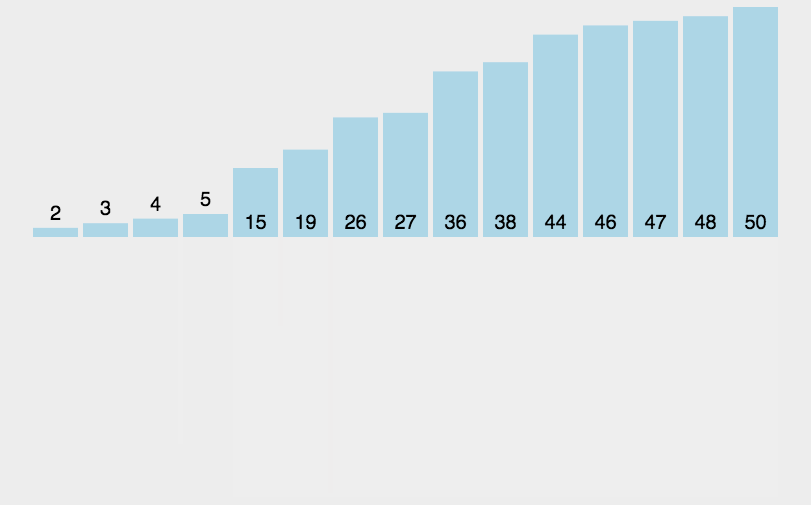
归并排序是一种常用且高效的排序算法，采用分治法的思想来对数组或列表进行排序。归并排序的基本思想是将数组分成较小的子数组，递归地对这些子数组进行排序，然后将它们合并在一起，产生最终的有序数组。

归并排序是一种递归算法，将输入数组不断地分割成较小的子数组，直到每个子数组只有一个元素，这一个元素是有序的。

然后，将排好序的子数组合并在一起，产生较大的有序子数组。

这个分割和合并的过程一直重复，直到整个数组都排序完毕。

归并排序是一种常用且高效的排序算法，采用分治法的思想来对数组或列表进行排序。归并排序的基本思想是将数组分成较小的子数组，递归地对这些子数组进行排序，然后将它们合并在一起，产生最终的有序数组。

归并排序是一种递归算法，将输入数组不断地分割成较小的子数组，直到每个子数组只有一个元素，这一个元素是有序的。

然后，将排好序的子数组合并在一起，产生较大的有序子数组。

这个分割和合并的过程一直重复，直到整个数组都排序完毕。

代码如下：

#include <iostream>

using namespace std;

const int N = 1e6 + 10;

int a[N], tmp[N];

void merge_sort(int q[], int l, int r)
{
    if (l >= r) return;

    int mid = l + r >> 1;

    merge_sort(q, l, mid), merge_sort(q, mid + 1, r);

    int k = 0, i = l, j = mid + 1;
    while (i <= mid && j <= r)
        if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];
        else tmp[k ++ ] = q[j ++ ];
    while (i <= mid) tmp[k ++ ] = q[i ++ ];
    while (j <= r) tmp[k ++ ] = q[j ++ ];

    for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];
}

int main()
{
    int n;
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);

    merge_sort(a, 0, n - 1);

    for (int i = 0; i < n; i ++ ) printf("%d ", a[i]);

    return 0;
}

逆序对的数量

给定一个长度为?n?的整数数列，请你计算数列中的逆序对的数量。

逆序对的定义如下：对于数列的第?i?个和第?j?个元素，如果满足?i<j 且?a[i]>a[j]，则其为一个逆序对；否则不是。

输入格式：

????????第一行包含整数?n，表示数列的长度。

????????第二行包含?n?个整数，表示整个数列。

输出格式：

????????输出一个整数，表示逆序对的个数。

数据范围：

????????1≤n≤100000,数列中的元素的取值范围?[1,10^9]

输入样例：

6
2 3 4 5 6 1

输出样例：

5

代码如下：

#include <iostream>

using namespace std;

typedef long long LL;

const int N = 1e5 + 10;

int a[N], tmp[N];

LL merge_sort(int q[], int l, int r)
{
    if (l >= r) return 0;

    int mid = l + r >> 1;

    LL res = merge_sort(q, l, mid) + merge_sort(q, mid + 1, r);

    int k = 0, i = l, j = mid + 1;
    while (i <= mid && j <= r)
        if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];
        else
        {
            res += mid - i + 1;
            tmp[k ++ ] = q[j ++ ];
        }
    while (i <= mid) tmp[k ++ ] = q[i ++ ];
    while (j <= r) tmp[k ++ ] = q[j ++ ];

    for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];

    return res;
}

int main()
{
    int n;
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);

    cout << merge_sort(a, 0, n - 1) << endl;

    return 0;
}