力扣hot100 完全平方数 完全背包 滚动数组 四平方和定理

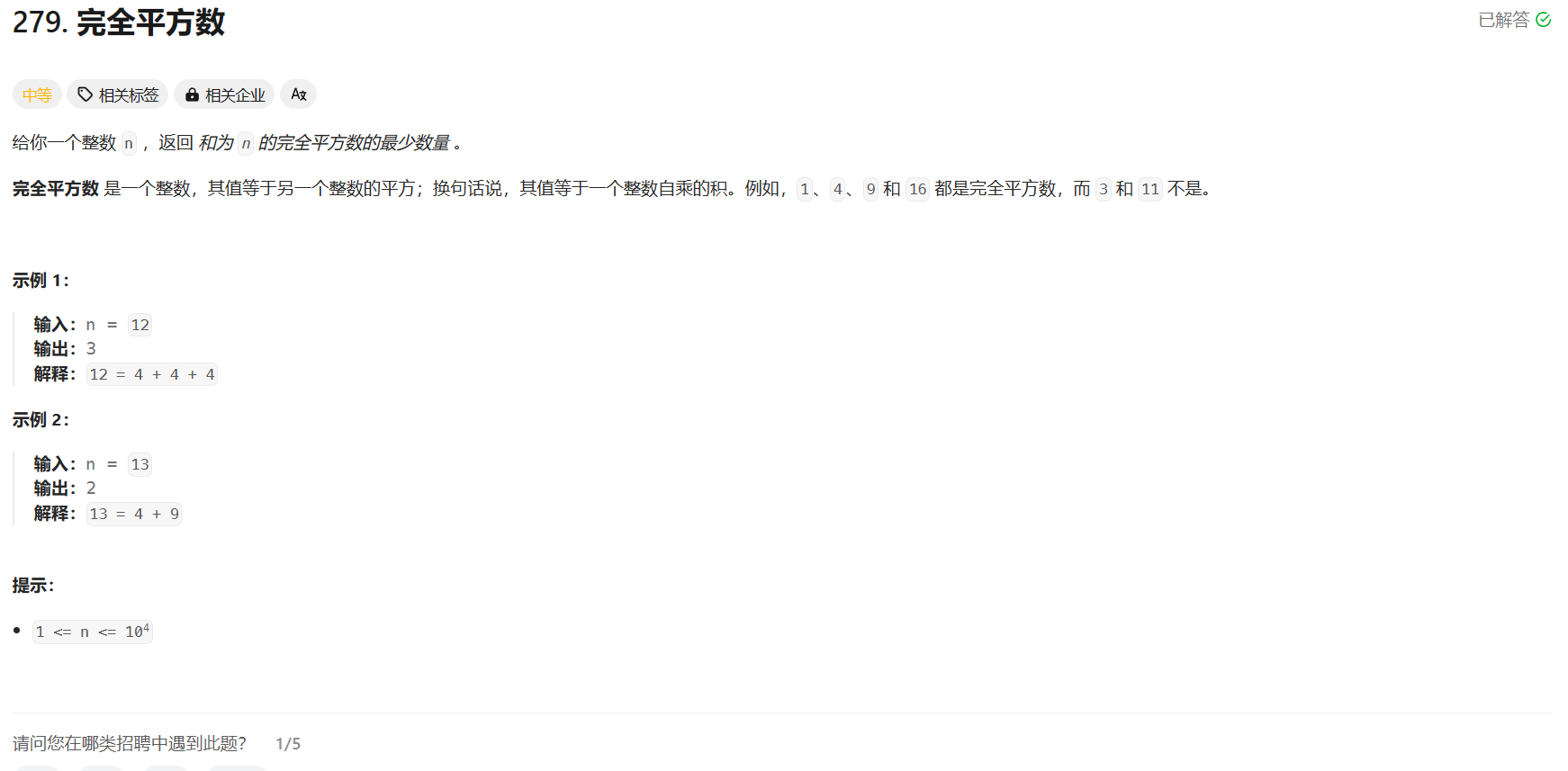
Problem: 279. 完全平方数

思路

👨?🏫 三叶神解

👨?🏫 数学解法

💖 完全背包

? 时间复杂度: $O(n^2\sqrt{n})$

class Solution {
    int INF = 0x3f3f3f3f;
	public int numSquares(int n)
	{
		List<Integer> list = new ArrayList<>();
		int t = 1;
		while (t * t <= n)
		{
			list.add(t * t);
			t++;
		}
		int m = list.size();
		int[][] f = new int[m + 1][n + 1];// f[i][j] 表示考虑前 i 个物品，凑出 j 所使用的最小元素个数
		Arrays.fill(f[0], INF);// 在 0 个物品中选，除了价值 0 外都是非法情况
		f[0][0] = 0;

		for (int i = 1; i <= m; i++)
		{
			int x = list.get(i - 1);// x 表示当前物品的 价值
			for (int j = 0; j <= n; j++)
			{
				f[i][j] = f[i - 1][j];// 不选当前物品
				for (int k = 1; k * x <= j; k++)// 选取 k 个当前物品
					if (f[i - 1][j - k * x] != INF)
						f[i][j] = Math.min(f[i][j], f[i - 1][j - k * x] + k);
			}
		}
		return f[m][n];
	}
}

💖 滚动数组优化

? 时间复杂度: $O(n\sqrt{n})$

class Solution {
	public int numSquares(int n)
	{
		int[] f = new int[n + 1];//f[i] 表示和为 i 的最小完全平方数和 的数量
		Arrays.fill(f, 0x3f3f3f3);
		f[0] = 0;
		for (int t = 1; t * t <= n; t++)
		{
			int x = t * t;
			for (int j = x; j <= n; j++)
				f[j] = Math.min(f[j], f[j - x] + 1);
		}
		return f[n];
	}
}

💖 四平方和定理

class Solution {
    public int numSquares(int n) {
        //判断是否是 1
        if (isSquare(n)) {
            return 1;
        }
        
        //判断是否是 4
        int temp = n;
        while (temp % 4 == 0) {
            temp /= 4;
        }
        if (temp % 8 == 7) {
            return 4;
        }

        //判断是否是 2
        for (int i = 1; i * i < n; i++) {
            if (isSquare(n - i * i)) {
                return 2;
            }
        }

        return 3;
    }

    //判断是否是平方数
    private boolean isSquare(int n) {
        int sqrt = (int) Math.sqrt(n);
        return sqrt * sqrt == n;
    }
}