manacher算法 求最长回文串

本题链接：用户登录

题目：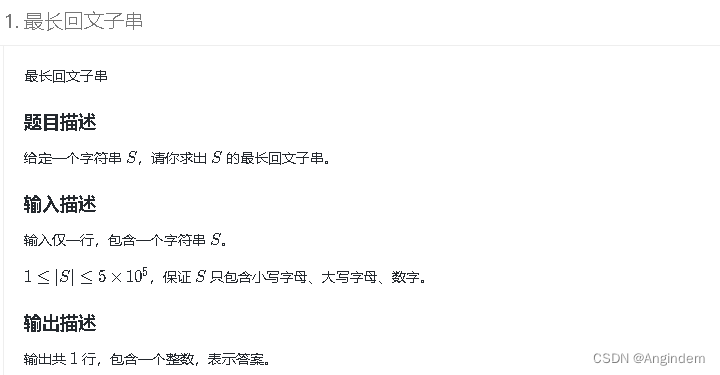

样例：

aa1ABA1b

思路：

? ? ? ? 根据题目意思，求出最长回文串，我们可以用模板 manacher 算法 求最长回文串。

????????manacher算法 求最长回文串 核心有两个步骤。

? ? ? ? 一、将字符串转化为? 奇数 长度的字符串，方便我们求回文串。

????????二、利用回文串对称性的特点，推导最长回文串长度。

????????

? ? ? ? 根据我们的核心开始一步一步来。

第一步，转化为奇数长度的字符串

????????我们把每个字符作为回文串的中心去处理。

????????我们只要在每个字符中间加入一个该字符串没有的符号，并且在头尾加入没出现过的不同的符号就行了（如下面这个字符串）。

? ? ? ? 根据给出的字符串?aa1ABA1b ?，我们将每个字符分隔起来，假设?用 ‘#’ 作为分隔符，头尾分别用 '$' 和 '^' 作为边界分隔符。

? ? ? ? 得到的转化字符串为 ：? ? ?$a#a#1#A#B#A#1#b^

? ? ? ? 这样我们就可以得到长度一定为奇数的字符串了。

????????新字符串长度?= 原长度 * 2 + 3；（’#’ 个数始终比原字符个数多 1）。

第二步，利用回文串对称性推导最长回文串

? ? ? ? 这里怎么利用回文串对称特性呢？

? ? ? ? 我们只要维护一个最长 回文串长度 来一步步推导就可以了。

? ? ? ? 我们看一下上面这个字符串? ?

? ? ? ? ? ? ? ? 新字符串：? ? ??$a#a#1#A#B#A#1#b^? ?

? ? ? ? ? ? ? ? ?原字符串：? ? ??aa1ABA1b

? ? ? ? ?假设我们找到了对称?的? ? 字符串?

??????? ?1ABA1? ?这个长度是? ?5?

????????我们再从新字符串看一下这个长度? ? ?#1#A#B#A#1#? ? ?这个长度是? 11

? ? ? ? 这里有一个规律，我们截取一下最右边的一半回文串：??? B#A#1#? ? ??这个长度是? 6

? ? ? ? 所以我们可以得到? ? ?新回文字符串的一半长度 - 1 == 回文字符串长度

? ? ? ?这就是我们利用回文串对称性推导最长回文串。

? ? ? ? 所以我们需要两个变量进行推导? ?一个是字符串中心点? mid? ?和一个 最右边的回文串长度 mr

? ? ? ? 这两个变量就是我们需要? ?维护 的一个 最长回文串 的变量

? ? ? ? 然后我们再用一个 p? 数组进行记录我们遍历整个字符串的过程中 最长回文串长度变化即可。

? ? ? ?

????????有人会疑问，如果不是对称的情况呢？就利用不到对称性了。

? ? ? ? 这里我们就 暴力向外扩张 求对称性 p 即可。

? ? ? ? 这里又有个疑问，如果对称的字符串不在我们的 维护的最长回文串里面呢？

? ? ? ? 所以这里有两种情况。

? ? ? ? 一种是：?p[ i ] 关于 最右回文串的对称字符串在 我们维护的 最长回文串?ml 、?mr 范围内

?????????????????????????那么 ans[ i ] = ans[ j ] (j 为对称子串的中心)。

????????????????????????其中 j? 等于 mid * 2 -? i 毕竟 (i + j) / 2 == mid? ?即? p[ i ] = p[ mid * 2 - i ]

? ? ? ? 一种是：不在范围内，因为(ml - mr) 是最右的回文串的边界，所以 p[ i ] 等于其对称子串在 ml-mr 中的最大半径。（因为其对称子串范围超过了 ml-mr，且 ml-mr 无法向右扩张，即 s[sr + 1] != s[sl - 1]。 那么此时 p[ i ] 就等于其对称子串在sl-sr范围内的半径? ?即? ? p[ i ] ==? mr - i?）

??

代码详解如下：

????????

#include <iostream>
#include <cstring>
#include <vector>
#define endl '\n'
#define int long long
#define IOS ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
using namespace std;
const int N = 2e7 + 10;
string a,b;
int n;


// 初始化转化字符串为 奇数 长度
inline void Init()
{
    b = "$#"; // 添加边界分隔符
    
    // 更新字符串
    for(int i = 0;i < n;++i)
    {
      b += a[i];
      b += '#';
    }

    b += "^"; // 添加边界分隔符
    n = b.size(); // 更新字符串新长度
}

// 马拉车算法求最长回文字符串长度
inline int Manacher()
{
    Init(); // 初始化

    vector<int>p(N,0); // 记录最长回文串

    int mr = 0,  mid; // 定义 mid 以及  mr 暂时还没发现最长回文串，所以 mr  == 0, mid  未知

    for(int i = 1;i < n;++i)
    {
        // 如果维护的最长回文串超出了 当前 i 字符串的 边界
        if(mr > i) p[i] = min(p[(mid << 1) - i],mr - i);  // 那么取相应的 对称情况的 有效的回文串长度
        else p[i] = 1;  // 如果没超出， 当前最长回文串长度就是 一个字符  长度就是 1

        while(b[i - p[i]] == b[i + p[i]]) ++p[i]; // 暴力扩张对称的回文串长度，并记录好

        // 如果 扩张后 存在当前回文串长度比之前维护的回文串长度还长
        // 那么更新最长回文串   mr   以及  mid 
        if(i + p[i] > mr)
        {
            mr = i + p[i];
            mid = i;
        }
    }
    
    int ans = 0;
    // 遍历记录数组 p 查找我们推导过程中出现的    最右最长回文串长度
    // 原字符串最长回文串长度  =   新字符串最右最长回文串长度 - 1    所以  p[i] - 1
    for(int i = 0;i < n;++i) ans = max(ans,p[i] - 1); 
  
    return ans;
}

signed main()
{
  IOS;
  cin >> a;
  n = a.size();

  int ans = Manacher();

  cout << ans << endl;


  return 0;
}

最后提交：