数据结构二：线性表之顺序表（不定长顺序表）的设计与实现

? ? ? ?本篇博客详细总结数据结构中的第一种结构:线性表之不定长顺序表，主要从以下几个方面梳理：线性表的定义、顺序表的概念、顺序表的基本操作：增删改查的基本思想及代码实现、基本操作的算法效率分析(时间复杂度和空间复杂度)、顺序表的优缺点适用场合，以及常见的面试题。

一、线性表的定义

? ? ? ?线性表（linear list）是n个具有相同特性的数据元素的有限序列。 线性表是一种在实际中广泛使用的数据结构，常见的线性表：顺序表、链表、栈、队列、字符串... 线性表在逻辑上是线性结构，也就说是连续的一条直线。但是在物理结构上并不一定是连续的， 线性表在物理上存储时，通常以数组和链式结构的形式存储。因此，线性表按照存储结构又分为：顺序表和链表。

二、顺序表之不定长顺序表（动态顺序表）

2.1 顺序表的基本概念及结构

? ? ? ?顺序表是用一段物理地址连续的存储单元依次存储数据元素的线性结构，只要确定好了存储线性表的起始位置，线性表中任一数据元素都可以随机存取，所以线性表的顺序存储结构是一种随机存取的储存结构，因为高级语言中的数组类型也是有随机存取的特性，所以通常我们都使用数组来描述数据结构中的顺序储存结构，即一般情况下采用数组存储。在数组上完成数据的增删查改。因此可以把顺序表就理解成数组。

2.2 顺序表的分类

顺序表一般可以分为：

1. 静态顺序表（也称为定长顺序表）：使用定长数组存储元素。
2. 动态顺序表（也称为不定长顺序表）：使用动态开辟的数组存储。

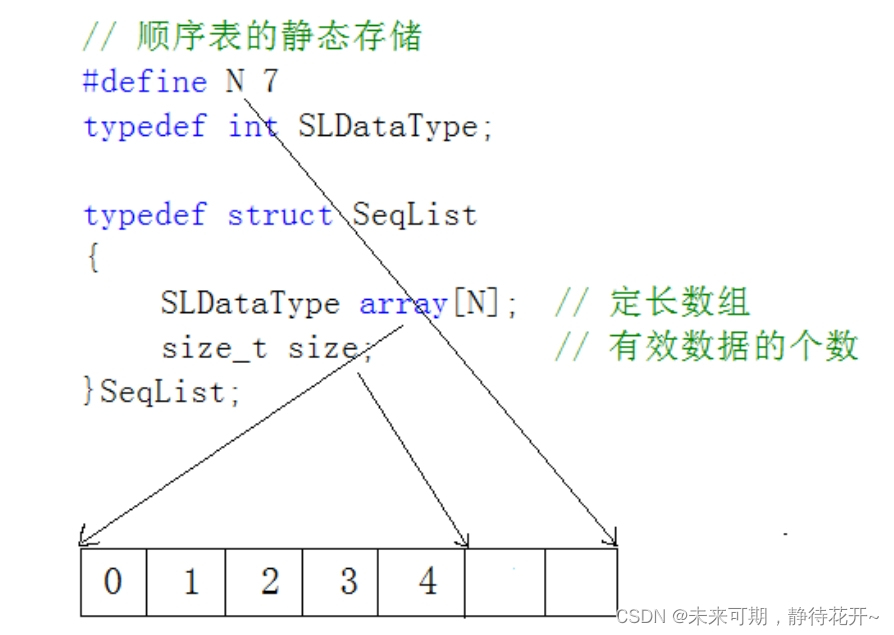
? ? ? 静态顺序表只适用于确定知道需要存多少数据的场景。静态顺序表的定长数组导致N定大了，空间开多了浪费，开少了不够用。所以现实中基本都是使用动态顺序表，根据需要动态的分配空间大小，所以下面我们实现动态顺序表。

?

2.2 接口实现（增删改查函数实现）及算法效率分析

? ? ? 引入的头文件

#include "SeqList.h"
#include<assert.h>
#include<stdlib.h>

顺序表的主要操作为增删改查，这里详细展示各个操作的思想和代码实现以及算法效率分析，主要接口函数如下所示：

//接口函数的设计
//1.初始化顺序表
void InitSeqList(SeqList* plist);
//2.销毁顺序表
void DestorySeqList(SeqList* plist);
//3.清空顺序表
void ClearSeqList(SeqList* plist);
//4.打印顺序表
void ShowSeqList(SeqList* plist);
//5.顺序表判满
Status IsFullSeqList(SeqList* plist);
//6.顺序表扩容
Status GrowSeqList(SeqList* plist);           // bool  GrowSeqList(SeqList* plist);
//7.顺序表判空
Status IsEmptySeqList(SeqList* plist);
//8.头插操作
Status InsertHead(SeqList* plist, ElemType val);
//9.尾插操作      
Status InsertTail(SeqList* plist, ElemType val);
//10.指定位置插入      posindex 插入的下标
Status InsertPosVal(SeqList* plist, int posindex, ElemType val);
//11.头删
Status DeleteHead(SeqList* plist);
//12.尾删
Status DeleteTail(SeqList* plist);
//13.指定位置删除
Status DeletePos(SeqList* plist, int posindex);
//14.删除指定元素（全部删除）
Status DeleteVal(SeqList* plist, ElemType val);
//15.查找某个元素，返回下标
int SearchVal(SeqList* plist, ElemType val);
//16.冒泡排序
void BubbleSort(SeqList* plist);
//17.二分查找（前提：数组完全有序）   非递归和递归实现
int BinarySearch0(SeqList* plist, ElemType val);
int BinarySearch1(SeqList* plist, ElemType val);
//18.将两个有序顺序表合并为一个有序顺序表
void MergeList(const SeqList* pla, const SeqList* plb, SeqList* plc);

?2.2.1 宏定义和类型重命名

? ? ? ?为方便代码复用和实际开发效率，通常会引入一些宏定义和类型重命名，如下代码所示：

#define TRUE 1
#define FALSE 0
#define OVERFLOW -1
#define LIST_INIT_CAPACITY 10    //动态顺序表的初始容量大小
#define LIST_GROW 2              //动态顺序表的扩容倍数

typedef int Status;             //状态 TRUE  FALSE 给c语言加入bool类型的方式
typedef int ElemType;           //数组元素类型

2.2.1 顺序表的设计

//顺序表类型的设计
typedef struct SeqList
{
	ElemType* data;    //动态申请的顺序表的起始地址
	size_t size;        //顺序表有效数据个数
	size_t capacity;    //顺序表的总容量
}SeqList;

2.2.2?顺序表的初始化

//1.初始化顺序表
void InitSeqList(SeqList* plist)
{
	assert(plist != NULL);
	plist->data = (ElemType*)malloc(sizeof(ElemType) * LIST_INIT_CAPACITY);
	assert(plist->data != NULL);
	plist->size = 0;
	plist->capacity = LIST_INIT_CAPACITY;
}

2.2.3 销毁顺序表

//2.销毁顺序表   释放堆内存
void DestorySeqList(SeqList* plist)
{
	assert(plist != NULL);
	free(plist->data);
	plist->data = NULL;          //防止出现野指针
}

2.2.4 清空顺序表

//3.清空顺序表    清除有效数据
void ClearSeqList(SeqList* plist)
{
	assert(plist != NULL);
	plist->size = 0;
}

2.2.5 打印顺序表

//4.打印顺序表
void ShowSeqList(SeqList* plist)
{
	assert(plist != NULL);
	int n = plist->size;
	for (int i = 0; i < plist->size; i++)
	{
		printf("%d ", plist->data[i]);
	}
	printf("\n");
}

2.2.6 顺序表判满

//5.顺序表判满
Status IsFullSeqList(SeqList* plist)
{
	assert(plist != NULL);
	return plist->size == plist->capacity;
}

2.2.7 顺序表扩容

//6.顺序表扩容
Status GrowSeqList(SeqList* plist)          // bool  GrowSeqList(SeqList* plist);
{
	assert(plist != NULL);
	if (plist == NULL)
		return FALSE;
	int newcapacity = plist->capacity * LIST_GROW;
	ElemType* tmp = (ElemType*)realloc(plist->data, newcapacity * sizeof(ElemType));
	if (tmp == NULL)
		return OVERFLOW;
	plist->data = tmp;
	plist->capacity = newcapacity;
	return TRUE;
}

2.2.8 顺序表判空

//7.顺序表判空
Status IsEmptySeqList(SeqList* plist)
{
	assert(plist != NULL);
	return plist->size == 0;
}

2.2.9 头插

//8.头插操作            时间复杂度：O(n)
Status InsertHead(SeqList* plist, ElemType val)
{
	assert(plist != NULL);
	if (IsFullSeqList(plist) && GrowSeqList(plist) != TRUE)
	{
		return OVERFLOW;
	}
	//进行移动数据
	for (int i = plist->size-1; i >0; i--)
	{
		plist->data[i + 1] = plist->data[i];
	}
	plist->data[0] = val;
	plist->size++;
	return TRUE;
}

2.2.10 尾插

//9.尾插操作        时间复杂度：O(1)
Status InsertTail(SeqList* plist, ElemType val)
{
	assert(plist != NULL);
	if (IsFullSeqList(plist) && GrowSeqList(plist) != TRUE)
	{
		return OVERFLOW;
	}
	plist->data[plist->size] = val;
	plist->size++;
	return TRUE;
}

2.2.11 指定位置插入

?

//10.指定位置插入      posindex 插入的下标            时间复杂度：O(n)
Status InsertPosVal(SeqList* plist, int posindex, ElemType val)
{
	assert(plist != NULL);
	if (posindex<0 || posindex>plist->size)
	{
		return FALSE;
	}
	if (IsFullSeqList(plist) && GrowSeqList(plist) != TRUE)
	{
		return OVERFLOW;
	}
	//进行移动数据
	for (int i = plist->size - 1; i >= posindex; i--)
	{
		plist->data[i + 1] = plist->data[i];
	}
	plist->data[posindex] = val;
	plist->size++;
	return TRUE;
}

2.2.12? 头删

//11.头删                   时间复杂度：O(n)
Status DeleteHead(SeqList* plist)
{
	assert(plist != NULL);
	if (IsEmptySeqList(plist))
	{
		return FALSE;
	}
	//进行移动数据
	for (int i = 1; i <= plist->size; i++)
	{
		plist->data[i - 1] = plist->data[i];
	}
	plist->size--;
	return TRUE;
}

2.2.13 尾删

//12.尾删                  时间复杂度：O(1)
Status DeleteTail(SeqList* plist)
{
	assert(plist != NULL);
	if (IsEmptySeqList(plist))
	{
		return FALSE;
	}
	plist->size--;  //存在局限性
	return TRUE;
}

2.2.14 指定位置删除

//13.指定位置删除         时间复杂度：O(n)
Status DeletePos(SeqList* plist, int posindex)
{
	assert(plist != NULL);
	if (posindex<0 || posindex>plist->size)
	{
		return FALSE;
	}
	//进行移动数据,元素覆盖
	for (int i = posindex; i > plist->size; i++)
	{
		plist->data[i] = plist->data[i + 1];
	}
	plist->size--;
	return TRUE;
}

2.2.15 删除指定元素

//14.删除指定元素（全部删除）          时间复杂度：O(n^2)
Status DeleteVal(SeqList* plist, ElemType val)
{
	if (plist->size == 0)
	{
		return FALSE;
	}
	else
	{
		int flag = FALSE;
		for (int i = 0; i <plist->size; )
		{
			if (plist->data[i] == val)
			{
				flag = TRUE;
				for (int j = i + 1; j < plist->size; j++)
				{
					plist->data[j - 1] = plist->data[j];
				}
				plist->size--;
			}
			else
			{
				i++;
			}
		}
		return flag;
	}
}

//补充练习Leetcode：成对出现数据，只有一个数据单独出现一次，
返回这个单独出现一次的数据的下标
/*解题思路：异或运算可以巧妙地解决出现一次的问题，
异或运算是位运算，计算效率更高，它是将两个数的二进制数按位进行异或，不同为1，相同为0
0与任何数异或结果为这个数，两个相同的数异或的结果是0，
出现偶数次的数异或两次必会被抵消，并且异或满足交换律，因此它与数组中的数字的顺序无关*/

int SearchOnlyOne(SeqList* plist)
{
	int res = 0;             //0异或一个数得到结果为这个数
	for (int i = 0; i < plist->size; i++)
	{
		res = res ^ plist->data[i];
	}
	return res;
}

2.2.16 查找某个元素

//15.查找某个元素，返回下标               时间复杂度：O(n)
int SearchVal(SeqList* plist, ElemType val)
{
	assert(plist != NULL);
	int index = -1;
	for (int i = 0; i < plist->size; i++)
	{
		if (plist->data[i] == val)
		{
			index = i;
			break;
		}
	}
	return index;
}

2.2.17 冒泡排序

//16.冒泡排序              时间复杂度：O(n^2)
void BubbleSort(SeqList* plist)
{
	assert(plist != NULL);
	if (plist->size == 0)
		return;
	bool flag = false;
	for (int i = 0; i < plist->size; i++)
	{
		for (int j = 0; j < plist ->size-i - 1; j++)
		{
			if (plist->data[j] > plist->data[j + 1])
			{
				ElemType tmp = plist->data[j];
				plist->data[j] = plist->data[j + 1];
				plist->data[j + 1] = tmp;
				flag = true;
			}
			
		}
		if (flag == false)
		{
			break;
		}
	}
}

2.2.18 二分查找

//17.二分查找（前提：数组完全有序）   非递归：时间复杂度O(logn)，空间复杂度：O(1)           和递归实现:时间复杂度是O(logn)，空间复杂度：O(n)   
int BinarySearch0(SeqList* plist, ElemType val)
{
	assert(plist != NULL);
	if (plist->size == 0)
		return;
	int left = 0, right = plist->size - 1;
	int index = -1;
	while (left <= right)
	{
		int midindex = (left + right) / 2;
		//int midindex = (left + right) >> 1;
		//int midindex=(right-left)/2+left;
		//int midindex=(right-left)>>1+left;
		if (plist->data[midindex] = val)
		{
			index = midindex;
		}
		else if (plist->data[midindex] > val)
		{
			right = midindex - 1;
		}
		else if(plist->data[midindex] < val)
		{
			left = midindex + 1;
		}
		return index;
	}
}


int SearchSection(SeqList* plist, int left, int right, ElemType val)
{
	if (left > right)
	{
		return -1;
	}
	int midindex = (left + right) / 2;
	if (plist->data[midindex] == val)
	{
		return midindex;
	}
	if (plist->data[midindex] > val)
	{
		return SearchSection(plist, left, midindex - 1, val);
	}
	else if (plist->data[midindex] < val)
	{
		return SearchSection(plist, midindex+1, right, val);
	}
}


int BinarySearch1(SeqList* plist, ElemType val)
{
	assert(plist != NULL);
	return SearchSection(plist, 0, plist->size - 1, val);
}

2.2.19 合并有序顺序表?

//18.将两个有序顺序表合并为一个有序顺序表:思想：谁小谁下来，谁++           时间复杂度O(m+n)，空间复杂度：O(n)  
void MergeList(const SeqList* pla, const SeqList* plb, SeqList* plc)
{
	assert(pla != NULL && plb != NULL && plc != NULL);
	int i=0, j=0, z=0;
	while (i < pla->size && j < plb->size)
	{
		if (pla->data[i] < plb->data[j])
		{
			//plc->data[z++] = pla->data[i++];
			InsertTail(plc, pla->data[i++]);//考虑 扩容问题
		}
		else 
		{
			//plc->data[z++] = plb->data[j++];
			InsertTail(plc, plb->data[j++]);//考虑 扩容问题
		}
	}
	if (i >= pla->size)
	{
		while (j < plb->size)
		{
			//plc->data[z++] = plb->data[j++];
			InsertTail(plc, plb->data[j++]);//考虑 扩容问题
		}
	}
	if (j > plb->size)
	{
		while(i < pla->size)
		{
			//plc->data[z++] = pla->data[i++];
			InsertTail(plc, pla->data[i++]);//考虑 扩容问题
		}
	}

}

2.3 顺序表优缺点总结

顺序表
1、可动态增长的数组
2、数据在数组中存储时必须是连续的
缺点:
1、中间或者头部的插入删除很慢，需要挪动数据。时间复杂度是0(N)

2、空间不够时，增容会有一定消耗和空间浪费。
优点:
1、随机访问。
2、缓存利用率比较高

2.4?顺序表的问题及思考

问题：

1. 中间/头部的插入删除，时间复杂度为O(N)

2. 增容需要申请新空间，拷贝数据，释放旧空间。会有不小的消耗。

3. 增容一般是呈2倍的增长，势必会有一定的空间浪费。例如当前容量为100，满了以后增容到 200，我们再继续插入了5个数据，后面没有数据插入了，那么就浪费了95个数据空间。

思考：如何解决以上问题呢？链表解决！！！

三、?数组相关面试题

1. 原地移除数组中所有的元素val，要求时间复杂度为O(N)，空间复杂度为O(1)。

2. 删除排序数组中的重复项。

3. 合并两个有序数组。