java数据结构与算法刷题-----LeetCode287. 寻找重复数
发布时间:2024年01月23日
| java数据结构与算法刷题目录(剑指Offer、LeetCode、ACM)-----主目录-----持续更新(进不去说明我没写完):https://blog.csdn.net/grd_java/article/details/123063846 |
|---|
| 解题思路 |
|---|
弗洛伊德判圈法,也就是快慢指针判圈法(龟兔赛跑算法),此算法分为两个步骤
- 判断是否有环,并得到快慢指针相遇的结点:慢指针每次走一格,快指针每次走两格,只要有环,必然会相遇。
- 获取构成环的结点:相遇后,让慢指针归0,快指针继续呆在相遇的地方,然后两个人依次一格一格的后移,最终再次相遇的地方,就是构成环的地方。
| 本题是数组题,如何想到用环形链表的解法呢? |
|---|
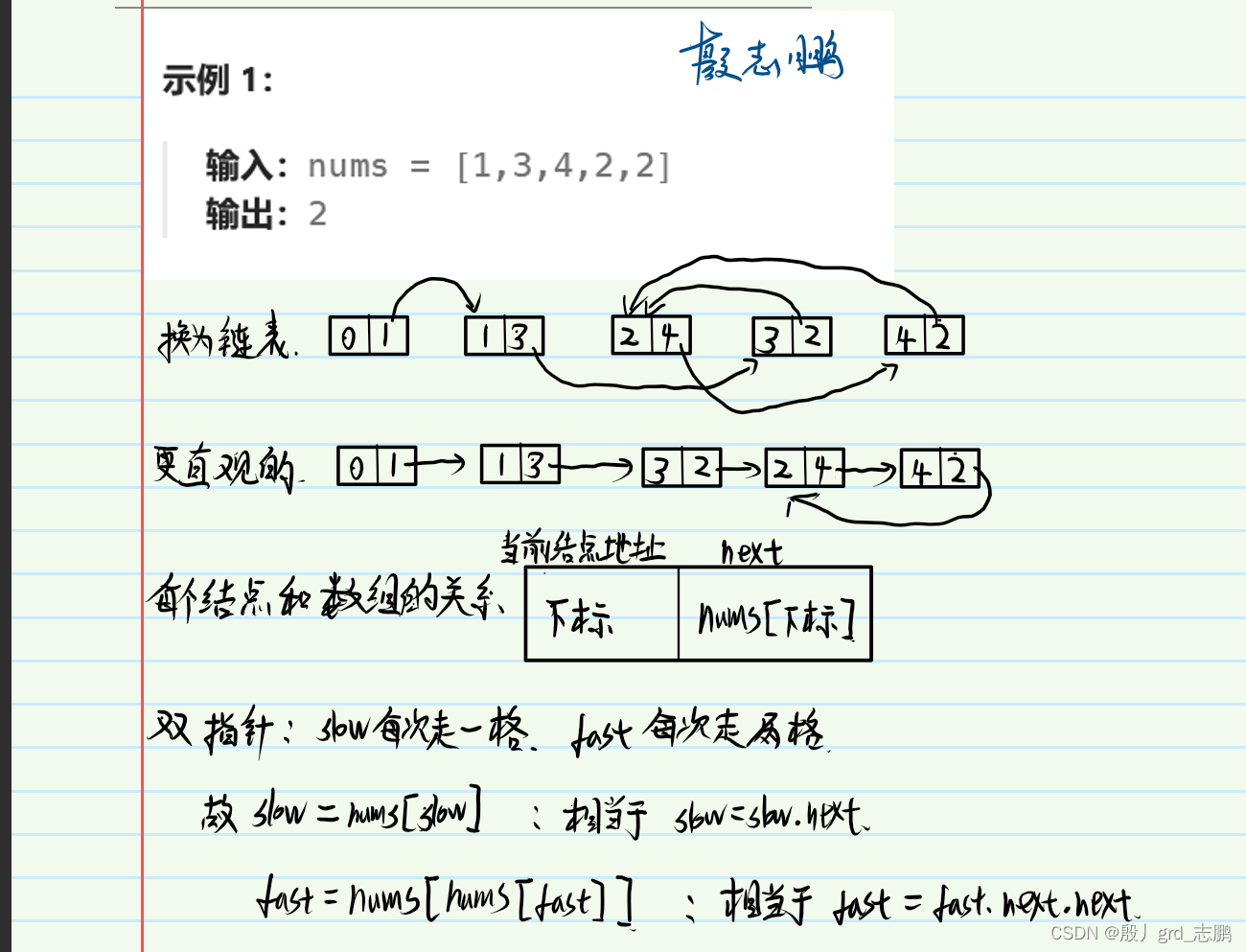
- 首先,这个题的数组,下标范围和取值范围是几乎相同的。因为下标范围在0 ~ n。取值范围是1 ~ n。那么下标和元素值是可以联立的。我们可以设置链表结点为[下标,元素值]来构成链表。因为有重复的元素值,那么这个链表比如有环,图解如下:
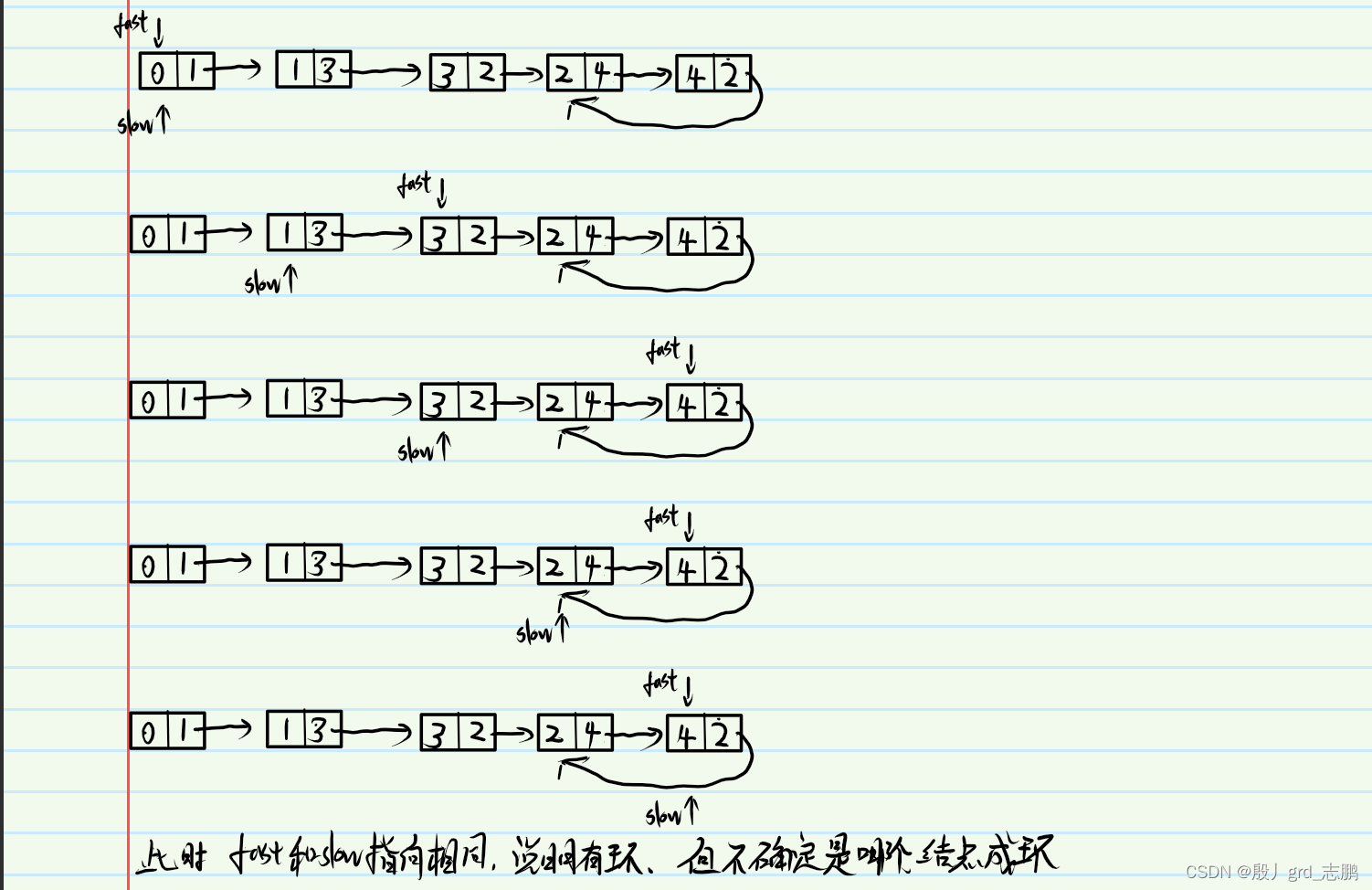
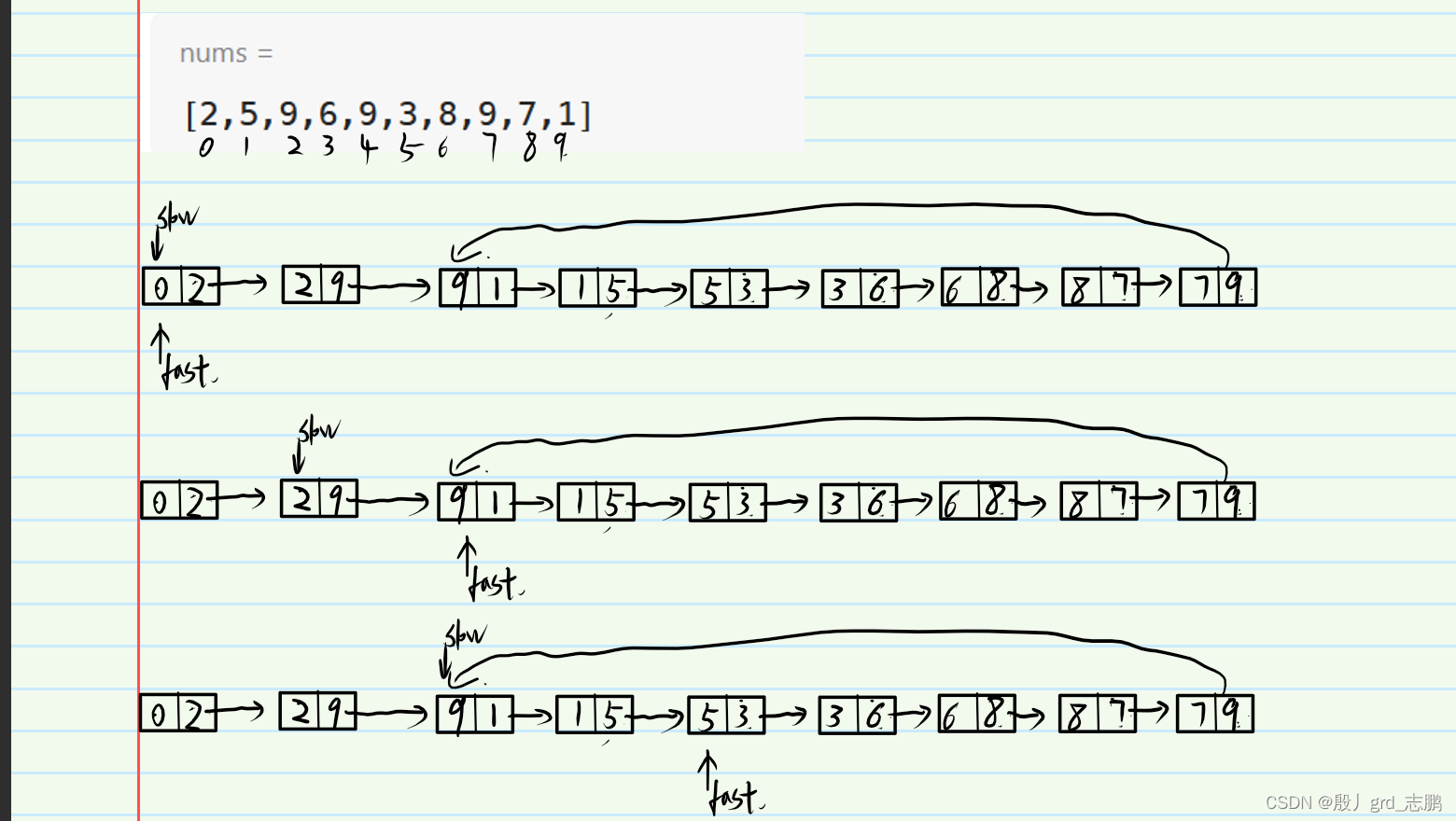
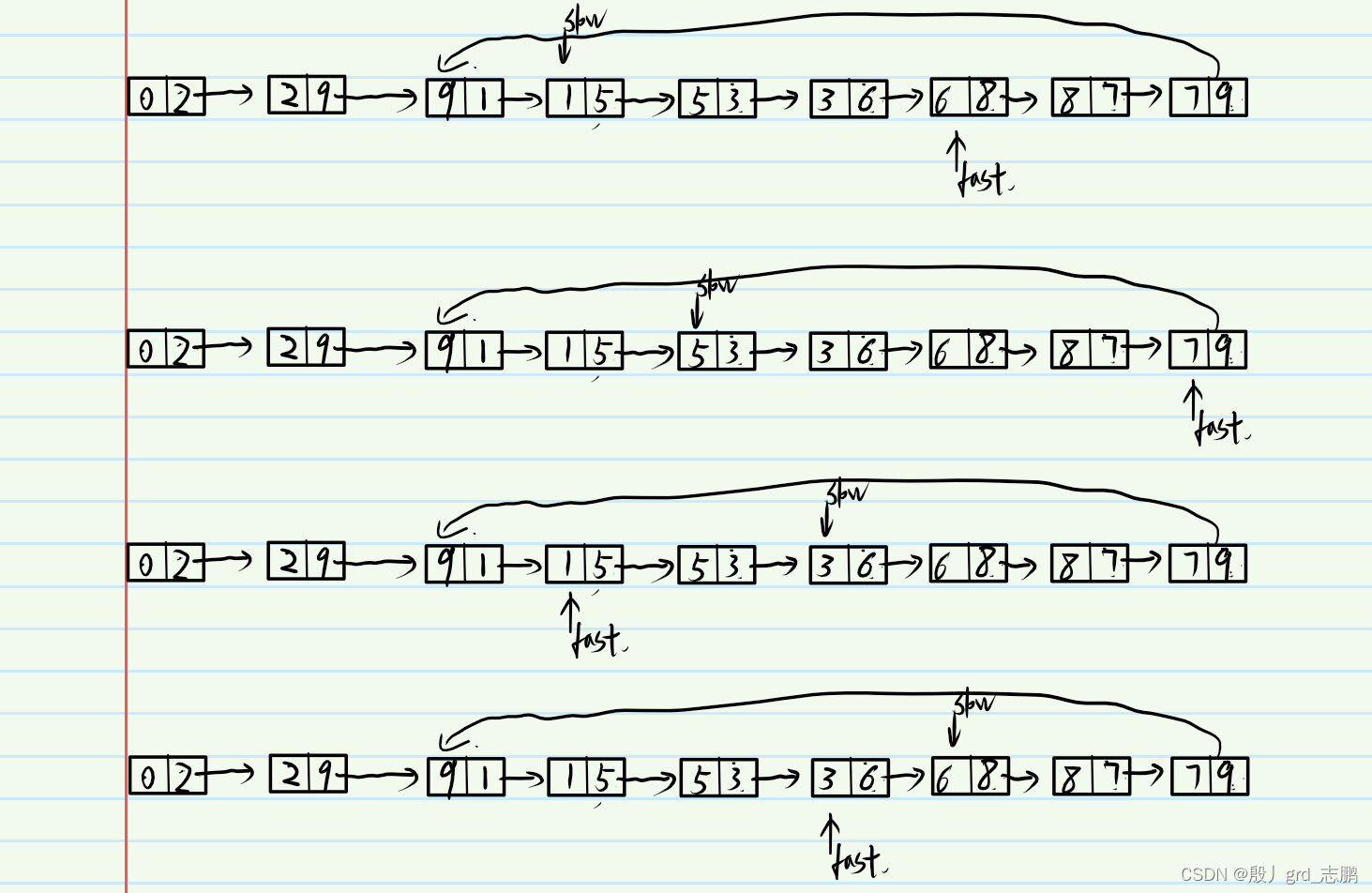
- 既然抽象出了链表,就可以使用弗洛伊德判圈法,先判断是否有环,然后获取相遇结点位置。下面给出两个例子
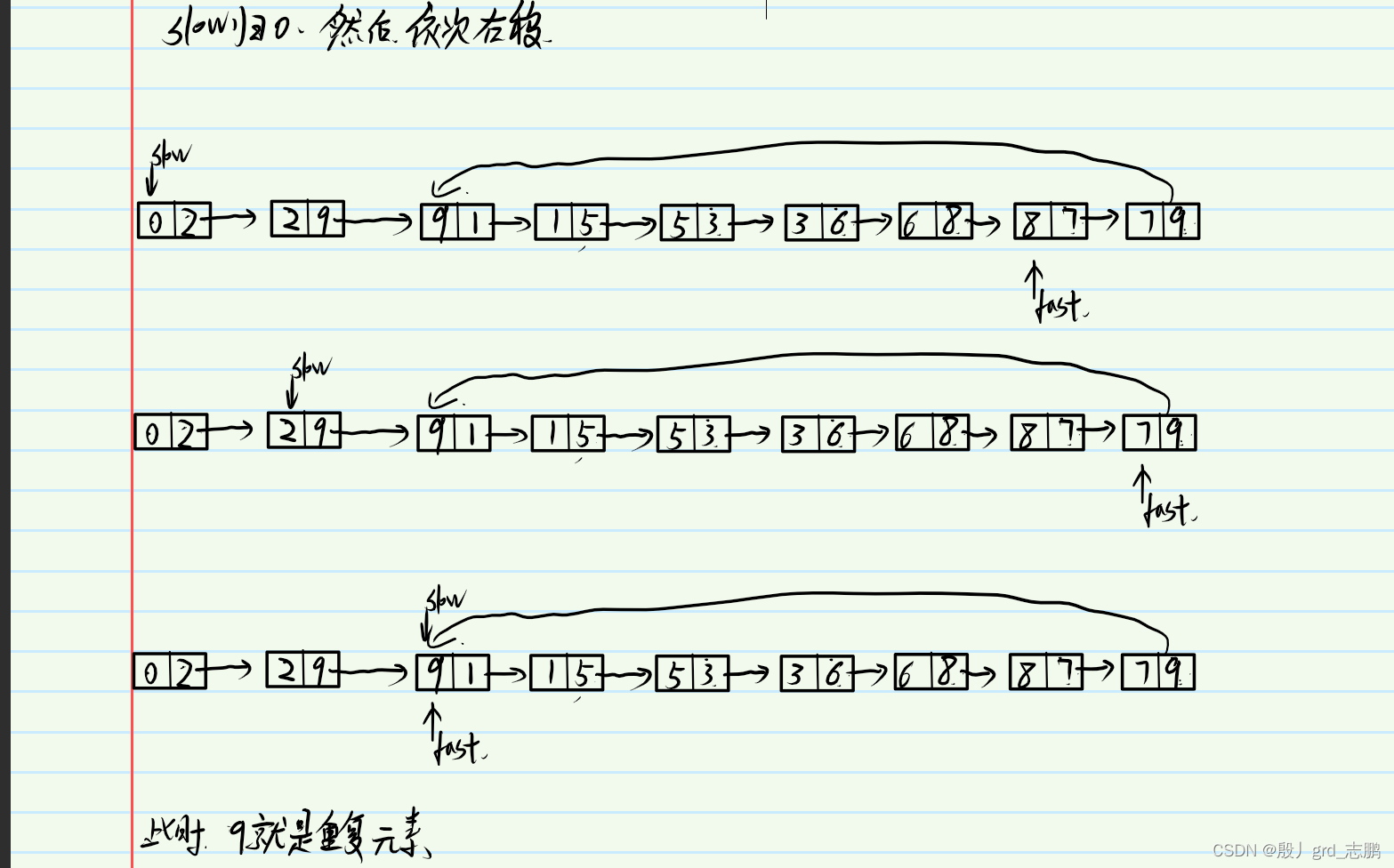
- 获取了相遇结点后,接下来就是慢指针归0,快指针继续在相遇的结点。然后两个指针依次一格一格的后移即可。图解如下
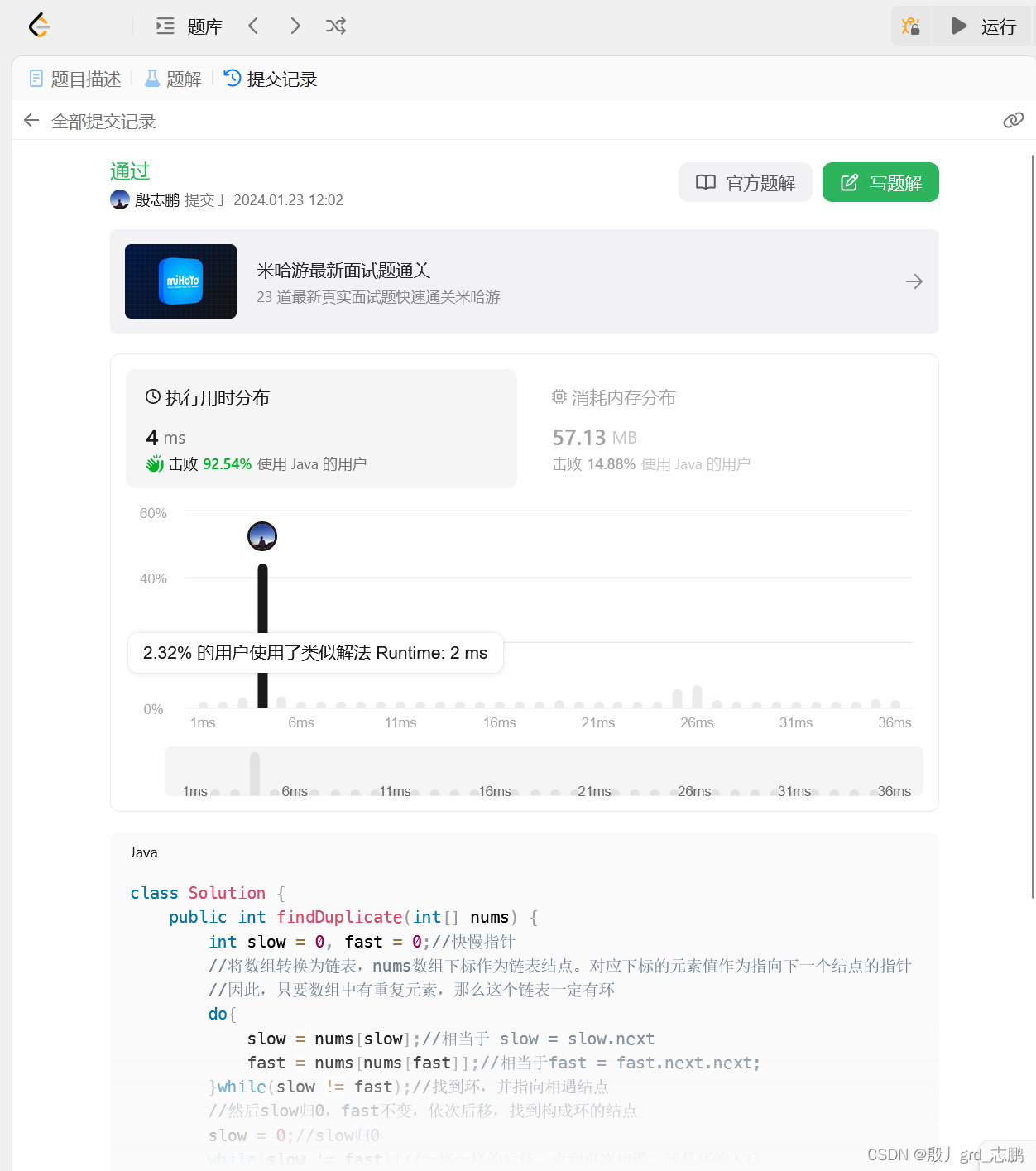
| 代码:时间复杂度O(n) 空间复杂度O(1) |
|---|
class Solution {
public int findDuplicate(int[] nums) {
int slow = 0, fast = 0;//快慢指针
//将数组转换为链表,nums数组下标作为链表结点。对应下标的元素值作为指向下一个结点的指针
//因此,只要数组中有重复元素,那么这个链表一定有环
do{
slow = nums[slow];//相当于 slow = slow.next
fast = nums[nums[fast]];//相当于fast = fast.next.next;
}while(slow != fast);//找到环,并指向相遇结点
//然后slow归0,fast不变,依次后移,找到构成环的结点
slow = 0;//slow归0
while(slow != fast){//一格一格的后移,直到再次相遇,就是环的入口
slow = nums[slow];
fast = nums[fast];
}
return slow;//最终返回这个结点值
}
}
文章来源:https://blog.csdn.net/grd_java/article/details/135767901
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 尚硅谷大数据项目《在线教育之实时数仓》笔记009
- 06.MySQL的用户和权限管理
- [强网杯 2019]Upload
- 桌面图标变成白色文件?学会这4个方法,轻松解决!
- Superset二次开发之环境部署(Docker版)
- C语言通过MSXML6.0读写XML文件(同时支持char[]和wchar_t[]字符数组)
- 数据工程实践:从网络抓取到API调用,解析共享单车所需要的数据
- UE5 C++(九)— 静态、动态加载类和资源
- 新年好,恭喜发财,喜气临门
- 聊聊PowerJob的RemoteEngine