代码随想录算法训练营第32天 | 122.买卖股票的最佳时机II 55. 跳跃游戏 45.跳跃游戏II

目录

122.买卖股票的最佳时机II?

💡解题思路

贪心算法

💻实现代码

55. 跳跃游戏?

💡解题思路

💻实现代码

45.跳跃游戏II

💡解题思路

# 方法一

方法二

💻实现代码

---

122.买卖股票的最佳时机II?

题目链接： 122.买卖股票的最佳时机 II

给定一个数组，它的第 ?i 个元素是一支给定股票第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1:

• 输入: [7,1,5,3,6,4]
• 输出: 7
• 解释: 在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4。随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。

示例 2:

• 输入: [1,2,3,4,5]
• 输出: 4
• 解释: 在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。

示例 ?3:

• 输入: [7,6,4,3,1]
• 输出: 0
• 解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。

提示：

• 1 <= prices.length <= 3 * 10 ^ 4
• 0 <= prices[i] <= 10 ^ 4

💡解题思路

本题首先要清楚两点：

• 只有一只股票！
• 当前只有买股票或者卖股票的操作

想获得利润至少要两天为一个交易单元。

贪心算法

这道题目可能我们只会想，选一个低的买入，再选个高的卖，再选一个低的买入.....循环反复。

如果想到其实最终利润是可以分解的，那么本题就很容易了！

如何分解呢？

假如第 0 天买入，第 3 天卖出，那么利润为：prices[3] - prices[0]。

相当于(prices[3] - prices[2]) + (prices[2] - prices[1]) + (prices[1] - prices[0])。

此时就是把利润分解为每天为单位的维度，而不是从 0 天到第 3 天整体去考虑！

那么根据 prices 可以得到每天的利润序列：(prices[i] - prices[i - 1]).....(prices[1] - prices[0])。

如图：

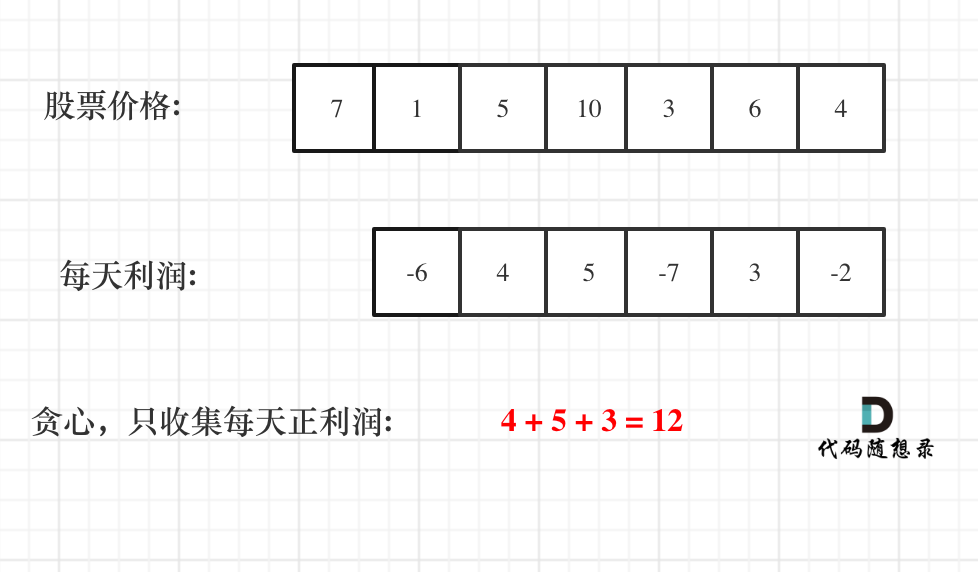
一些同学陷入：第一天怎么就没有利润呢，第一天到底算不算的困惑中。

第一天当然没有利润，至少要第二天才会有利润，所以利润的序列比股票序列少一天！

从图中可以发现，其实我们需要收集每天的正利润就可以，收集正利润的区间，就是股票买卖的区间，而我们只需要关注最终利润，不需要记录区间。

那么只收集正利润就是贪心所贪的地方！

局部最优：收集每天的正利润，全局最优：求得最大利润。

局部最优可以推出全局最优，找不出反例，试一试贪心！

💻实现代码

class Solution {
    public int maxProfit(int[] prices) {
        int profit=0;
        for(int i=1;i<prices.length;i++){
            profit+=Math.max(prices[i]-prices[i-1],0);
        }
        return profit;
    }
}

55. 跳跃游戏?

题目链接：55. 跳跃游戏

给定一个非负整数数组，你最初位于数组的第一个位置。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个位置。

示例 ?1:

• 输入: [2,3,1,1,4]
• 输出: true
• 解释: 我们可以先跳 1 步，从位置 0 到达 位置 1, 然后再从位置 1 跳 3 步到达最后一个位置。

示例 ?2:

• 输入: [3,2,1,0,4]
• 输出: false
• 解释: 无论怎样，你总会到达索引为 3 的位置。但该位置的最大跳跃长度是 0 ， 所以你永远不可能到达最后一个位置。

💡解题思路

贪心算法局部最优解：每次取最大跳跃步数（取最大覆盖范围），整体最优解：最后得到整体最大覆盖范围，看是否能到终点。

如图：

i 每次移动只能在 cover 的范围内移动，每移动一个元素，cover 得到该元素数值（新的覆盖范围）的补充，让 i 继续移动下去。

而 cover 每次只取 max(该元素数值补充后的范围, cover 本身范围)。

如果 cover 大于等于了终点下标，直接 return true 就可以了。

💻实现代码

class Solution {
    public boolean canJump(int[] nums) {
        if(nums.length==1){
            return true;
        }
        int res=0;
        for(int i=0;i<=res;i++){
            res=Math.max(res,i+nums[i]);
            if(res>=nums.length-1){
                return true;
            }
        }
        return false;
    }
}

45.跳跃游戏II

题目链接：45.跳跃游戏 II

给定一个非负整数数组，你最初位于数组的第一个位置。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

你的目标是使用最少的跳跃次数到达数组的最后一个位置。

示例:

• 输入: [2,3,1,1,4]
• 输出: 2
• 解释: 跳到最后一个位置的最小跳跃数是 2。从下标为 0 跳到下标为 1 的位置，跳 ?1? 步，然后跳 ?3? 步到达数组的最后一个位置。

说明: 假设你总是可以到达数组的最后一个位置。

💡解题思路

贪心的思路，局部最优：当前可移动距离尽可能多走，如果还没到终点，步数再加一。整体最优：一步尽可能多走，从而达到最少步数。

所以真正解题的时候，要从覆盖范围出发，不管怎么跳，覆盖范围内一定是可以跳到的，以最小的步数增加覆盖范围，覆盖范围一旦覆盖了终点，得到的就是最少步数！

这里需要统计两个覆盖范围，当前这一步的最大覆盖和下一步最大覆盖。

如果移动下标达到了当前这一步的最大覆盖最远距离了，还没有到终点的话，那么就必须再走一步来增加覆盖范围，直到覆盖范围覆盖了终点。

如图：

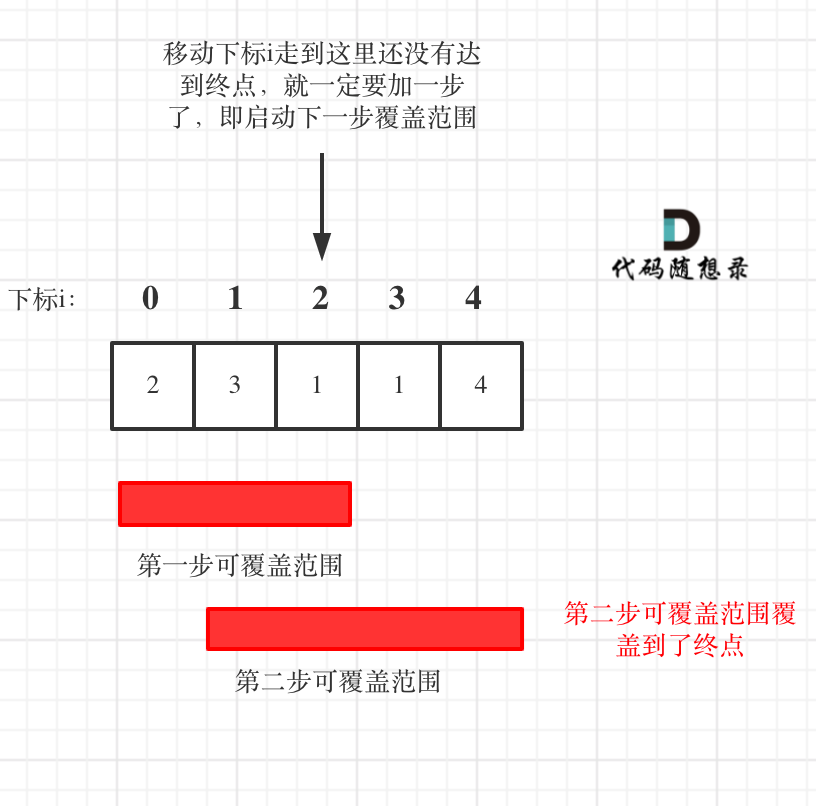
图中覆盖范围的意义在于，只要红色的区域，最多两步一定可以到！（不用管具体怎么跳，反正一定可以跳到）

方法一

从图中可以看出来，就是移动下标达到了当前覆盖的最远距离下标时，步数就要加一，来增加覆盖距离。最后的步数就是最少步数。

这里还是有个特殊情况需要考虑，当移动下标达到了当前覆盖的最远距离下标时

• 如果当前覆盖最远距离下标不是是集合终点，步数就加一，还需要继续走。
• 如果当前覆盖最远距离下标就是是集合终点，步数不用加一，因为不能再往后走了。

方法二

依然是贪心，思路和方法一差不多，代码可以简洁一些。

针对于方法一的特殊情况，可以统一处理，即：移动下标只要遇到当前覆盖最远距离的下标，直接步数加一，不考虑是不是终点的情况。

想要达到这样的效果，只要让移动下标，最大只能移动到 nums.size - 2 的地方就可以了。

因为当移动下标指向 nums.size - 2 时：

• 如果移动下标等于当前覆盖最大距离下标， 需要再走一步（即 ans++），因为最后一步一定是可以到的终点。（题目假设总是可以到达数组的最后一个位置），如图：

  

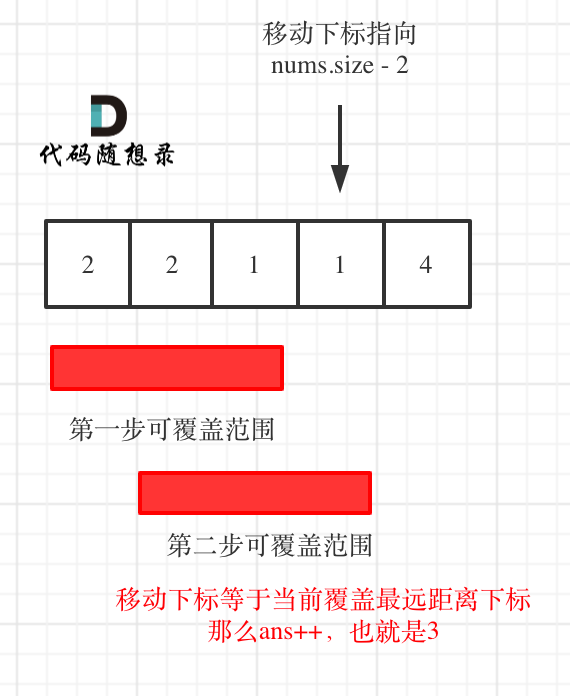
• 如果移动下标不等于当前覆盖最大距离下标，说明当前覆盖最远距离就可以直接达到终点了，不需要再走一步。如图：

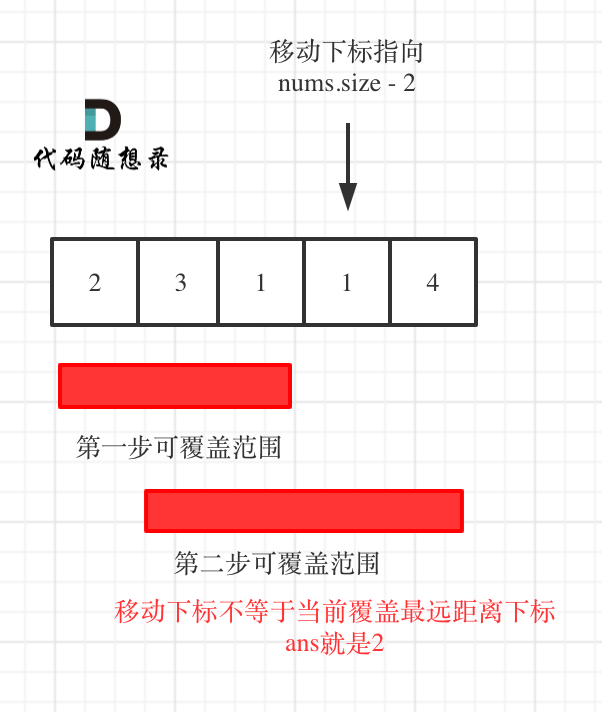
💻实现代码

class Solution {
    public int jump(int[] nums) {
        if(nums.length==0||nums.length==1||nums==null){
            return 0;
        }
        int count=0 ;
        int maxjump=0;
        int curjump=0;
        for(int i=0;i<nums.length;i++){
            maxjump=Math.max(maxjump,nums[i]+i);
            if(maxjump>=nums.length-1){
                count++;
                break;
            }
            if(i==curjump){
                curjump=maxjump;
                count++;
            }
        }
        return count;
    }
}