二分查找——OJ题（二）

📘北尘_：个人主页
🌎个人专栏:《Linux操作系统》《经典算法试题 》《C++》 《数据结构与算法》

??走在路上，不忘来时的初心

---

一、点名

1、题目讲解

2、算法原理

关于这道题中，时间复杂度为 O(N) 的解法有很多种，?且也是?较好想的，这?就不再赘述。
本题只讲解?个最优的?分法，来解决这个问题。
在这个升序的数组中，我们发现：
? 在第?个缺失位置的左边，数组内的元素都是与数组的下标相等的；
? 在第?个缺失位置的右边，数组内的元素与数组下标是不相等的。

3、代码实现

class Solution {
public:
    int takeAttendance(vector<int>& records) {
        int left=0,right=records.size()-1;
        while(left<right)
        {
            int mid=left+(right-left)/2;
            if(records[mid]==mid) left=mid+1;
            else right=mid;
        }
        return records[left]==left?left+1:left;
    }
};

---

二、搜索旋转排序数组中的最?值

1、题目讲解

2、算法原理

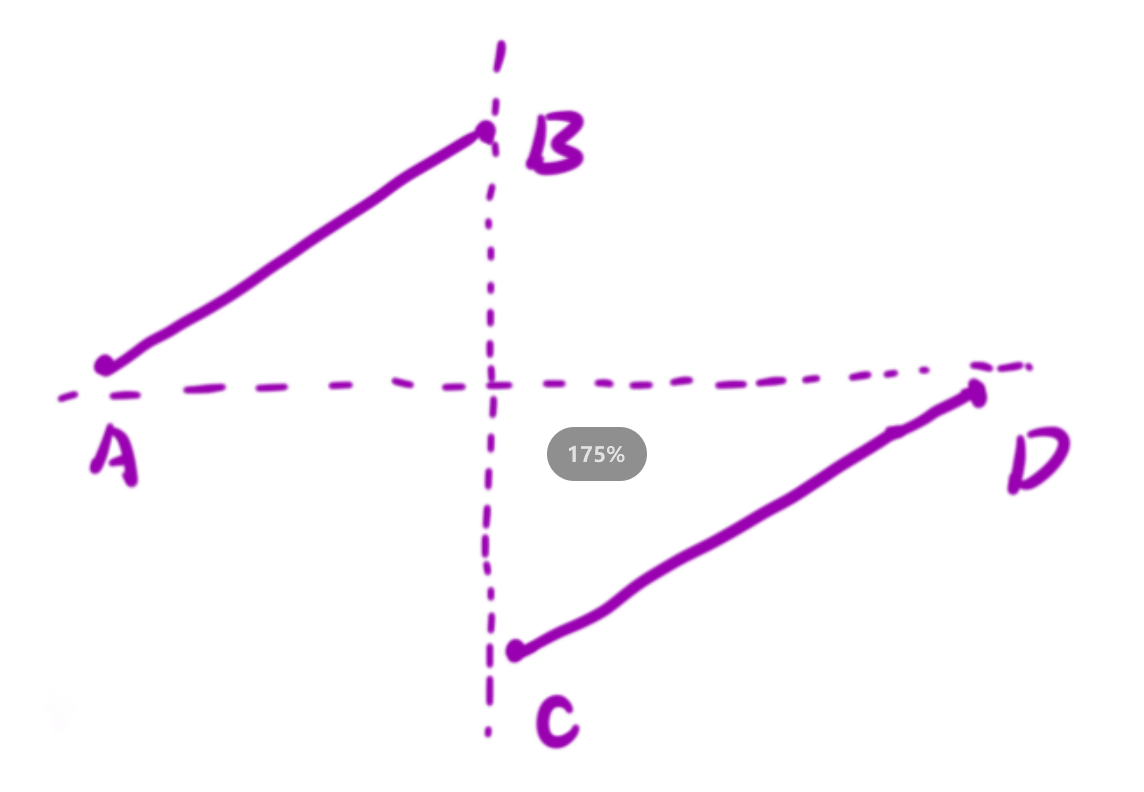
其中 C 点就是我们要求的点。
?分的本质：找到?个判断标准，使得查找区间能够?分为?。
通过图像我们可以发现， [A，B] 区间内的点都是严格?于 D 点的值的， C 点的值是严格?于 D 点的值的。但是当 [C，D] 区间只有?个元素的时候， C 点的值是可能等于 D 点的值的。
因此，初始化左右两个指针 left ， right ：
然后根据 mid 的落点，我们可以这样划分下?次查询的区间：
? 当 mid 在 [A，B] 区间的时候，也就是 mid 位置的值严格?于 D 点的值，下?次查询区间在 [mid + 1，right] 上；
? 当 mid 在 [C，D] 区间的时候，也就是 mid 位置的值严格?于等于 D 点的值，下次查询区间在 [left，mid] 上。
当区间?度变成 1 的时候，就是我们要找的结果。

3、代码实现

class Solution {
public:
    int findMin(vector<int>& nums) {
        int left=0,right=nums.size()-1,n=nums.size();
        while(left<right)
        {
            int mid=left+(right-left)/2;
            if(nums[mid]>nums[n-1]) left=mid+1;
            else right=mid;
        }
        return nums[left];

    }
};

---

三、寻找峰值

1、题目讲解

2、算法原理

寻找?段性：
任取?个点 i ，与下?个点 i + 1 ，会有如下两种情况：
? arr[i] > arr[i + 1] ：此时「左侧区域」?定会存在?峰（因为最左侧是负?穷），那么我们可以去左侧去寻找结果；
? arr[i] < arr[i + 1] ：此时「右侧区域」?定会存在?峰（因为最右侧是负?穷），那么我们可以去右侧去寻找结果。

3、代码实现

class Solution {
public:
    int findPeakElement(vector<int>& nums) {
        int left=0,right=nums.size()-1;
        while(left<right)
        {
            int mid=left+(right-left)/2;
            if(nums[mid]<nums[mid+1]) left=mid+1;
            else right=mid;
        }
        return left;
    }
};

---

四、山峰数组的峰顶

1、题目讲解

2、算法原理

1. 分析峰顶位置的数据特点，以及?峰两旁的数据的特点：
   ? 峰顶数据特点： arr[i] > arr[i - 1] && arr[i] > arr[i + 1] ；
   ? 峰顶左边的数据特点： arr[i] > arr[i - 1] && arr[i] < arr[i + 1] ，也就是呈现上升趋势；
   ? 峰顶右边数据的特点： arr[i] < arr[i - 1] && arr[i] > arr[i + 1] ，也就是呈现下降趋势。
2. 因此，根据 mid 位置的信息，我们可以分为下?三种情况：
   ? 如果 mid 位置呈现上升趋势，说明我们接下来要在 [mid + 1, right] 区间继续搜索；
   ? 如果 mid 位置呈现下降趋势，说明我们接下来要在 [left, mid - 1] 区间搜索；
   ? 如果 mid 位置就是?峰，直接返回结果。

3、代码实现

class Solution {
public:
    int peakIndexInMountainArray(vector<int>& arr) {
        int left=1,right=arr.size()-2;
        while(left<right)
        {
            int mid=left+(right-left+1)/2;
            if(arr[mid]>arr[mid-1]) left=mid;
            else right=mid-1;
        }
        return left;
    }
};

---