斯坦福 Stats60：21 世纪的统计学：第十章到第十四章

第十章：量化效应和设计研究

原文：statsthinking21.github.io/statsthinking21-core-site/ci-effect-size-power.html

译者：飞龙

协议：CC BY-NC-SA 4.0

在上一章中，我们讨论了如何使用数据来检验假设。这些方法提供了一个二元答案：我们要么拒绝要么未能拒绝零假设。然而，这种决定忽略了一些重要的问题。首先，我们想知道答案有多大的不确定性（无论结果如何）。此外，有时我们没有一个明确的零假设，因此我们想看到与数据一致的估计范围。其次，我们想知道效应实际上有多大，因为正如我们在上一章中的减重示例中看到的，统计上显著的效应未必是实际上重要的效应。

在本章中，我们将讨论解决这两个问题的方法：置信区间提供我们对估计的不确定性的度量，以及效应大小提供了一种标准化的方式来理解效应的大小。我们还将讨论统计功效的概念，它告诉我们我们有多大可能发现实际存在的任何真实效应。

10.1 置信区间

到目前为止，本书中我们一直专注于估计单个数值统计量。例如，假设我们想要估计 NHANES 数据集中成年人的平均体重，因此我们从数据集中抽取样本并估计平均值。在这个样本中，平均体重为 79.92 公斤。我们将这称为点估计，因为它为我们提供了一个单一的数字来描述我们对总体参数的估计。然而，根据我们之前对抽样误差的讨论，我们知道对这个估计存在一定的不确定性，这由标准误差描述。您还应该记住，标准误差由两个组成部分确定：总体标准差（分子）和样本大小的平方根（分母）。总体标准差是一个通常未知但固定的参数，不在我们的控制范围内，而样本大小在我们的控制范围内。因此，我们可以通过增加样本大小来减少对估计的不确定性-直到整个人口规模的极限，此时没有任何不确定性，因为我们可以直接从整个人口的数据中计算出总体参数。

我们经常希望有一种更直接地描述我们对统计估计的不确定性的方法，这可以通过使用置信区间来实现。大多数人通过政治民意调查中“误差范围”的概念熟悉置信区间。这些调查通常试图提供一个在+/- 3%内准确的答案。例如，当估计候选人在选举中以 9 个百分点的优势获胜，误差范围为 3 时，他们将获胜的百分比估计在 6-12 个百分点之间。在统计学中，我们将这种数值范围称为置信区间，它提供了一系列与我们的样本数据一致的参数估计值，而不仅仅是基于数据给出一个单一的估计。置信区间越宽，我们对参数估计的不确定性就越大。

置信区间因其含义常常令人困惑，主要是因为它们的含义并不是我们直觉上认为的含义。如果我告诉你我已经计算出了我的统计量的“95%置信区间”，那么似乎自然地认为我们可以有 95%的信心，真实的参数值落在这个区间内。然而，正如我们在整个课程中将看到的那样，统计学中的概念通常并不是我们认为它们应该是的。在置信区间的情况下，我们不能以这种方式解释它们，因为总体参数具有固定值 - 它要么在区间内，要么不在区间内，因此谈论发生这种情况的概率是没有意义的。置信区间的发明者 Jerzy Neyman 说过：

“参数是一个未知的常数，关于它的值不可能做出概率陈述。”(J. Neyman 1937)

相反，我们必须从与我们观察假设检验相同的角度来看待置信区间过程：作为一个长期来看，它将允许我们以特定概率做出正确的陈述的过程。因此，95%置信区间的正确解释是，它是一个区间，将在 95%的时间内包含真实的总体均值，事实上，我们可以使用模拟来确认这一点，如下所示。

均值的置信区间计算如下：

$$CI=\text{点估计}\pm \text{临界值}?\text{标准误差}$$

其中临界值由估计的抽样分布确定。那么，重要的问题是我们如何获得我们的估计值的抽样分布。

10.1.1 正态分布下的置信区间

如果我们知道总体标准差，那么我们可以使用正态分布来计算置信区间。我们通常不知道，但对于 NHANES 数据集的示例，我们知道，因为我们将整个数据集视为总体（体重为 21.3）。

假设我们想要计算均值的 95%置信区间。临界值将是标准正态分布的值，这些值捕获了分布的 95%；这些值只是分布的第 2.5 百分位数和第 97.5 百分位数，我们可以使用统计软件计算出来，结果为$\pm 1.96$。因此，均值（$\bar{X}$）的置信区间是：

$$CI=\bar{X}\pm 1.96?SE$$

使用样本的估计均值（79.92）和已知的总体标准差，我们可以计算出置信区间为[77.28,82.56]。

10.1.2 使用 t 分布的置信区间

如上所述，如果我们知道总体标准差，那么我们可以使用正态分布来计算置信区间。然而，一般情况下我们不知道 - 在这种情况下，t分布更适合作为抽样分布。请记住，t 分布比正态分布略宽，特别是对于较小的样本，这意味着置信区间将比使用正态分布时稍微宽一些。这包括了在我们基于小样本估计参数时产生的额外不确定性。

我们可以以与上面正态分布示例类似的方式计算 95%置信区间，但临界值由适当自由度的t分布的第 2.5 百分位数和第 97.5 百分位数确定。因此，均值（$\bar{X}$）的置信区间是：

$$CI=\bar{X}\pm t_{crit}?SE$$

其中$t_{crit}$是临界 t 值。对于 NHANES 体重示例（样本量为 250），置信区间将是 79.92 +/- 1.97 * 1.41 [77.15 - 82.69]。

请记住，这并不告诉我们真实总体值落入此区间的概率，因为它是一个固定参数（在这种情况下，我们知道是 81.77，因为我们在这种情况下有整个总体），它要么在这个特定的区间内，要么不在（在这种情况下，它在）。相反，它告诉我们，从长远来看，如果我们使用这个程序计算置信区间，有 95%的时间置信区间将捕获真实的总体参数。

我们可以使用 NHANES 数据作为我们的总体；在这种情况下，我们知道总体参数的真实值，因此我们可以看到在许多不同的样本中置信区间最终捕获该值的频率。图 10.1 显示了从 NHANES 数据集中计算的估计平均体重的 100 个样本的置信区间。其中有 95 个捕获了真实的总体平均体重，表明置信区间程序的执行效果如预期。

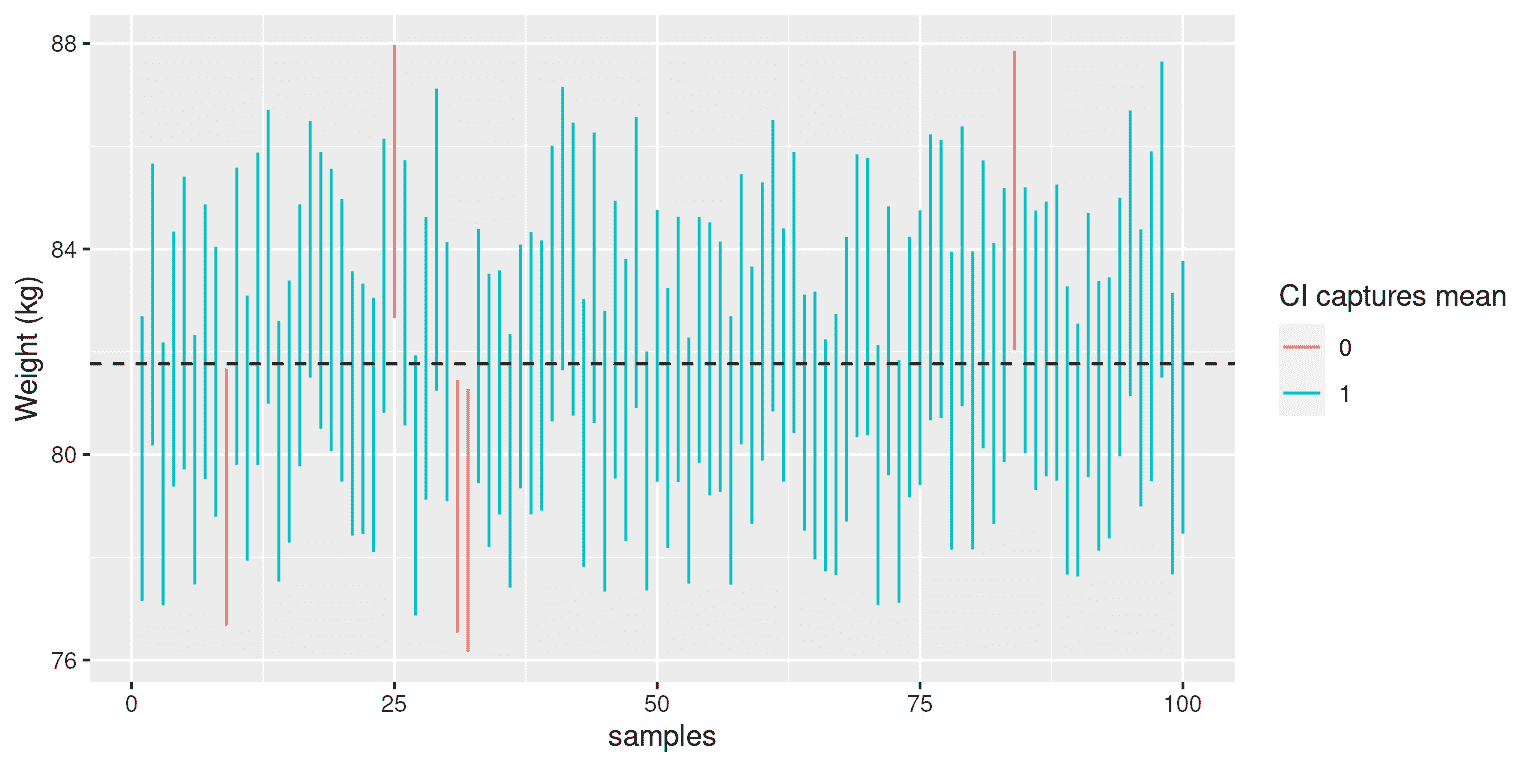
图 10.1：从 NHANES 数据集中重复取样，为每个样本计算了平均值的 95%置信区间。红色区间未捕获真实的总体均值（显示为虚线）。

10.1.3 置信区间和样本量

由于标准误差随样本量的减少而减少，因此随着样本量的增加，置信区间应该变得更窄，为我们的估计提供逐渐更紧的界限。图 10.2 显示了置信区间在体重示例中随样本量变化的示例。从图中可以明显看出，随着样本量的增加，置信区间变得越来越紧，但增加样本提供的回报递减，这与置信区间项的分母与样本量的平方根成比例的事实一致。

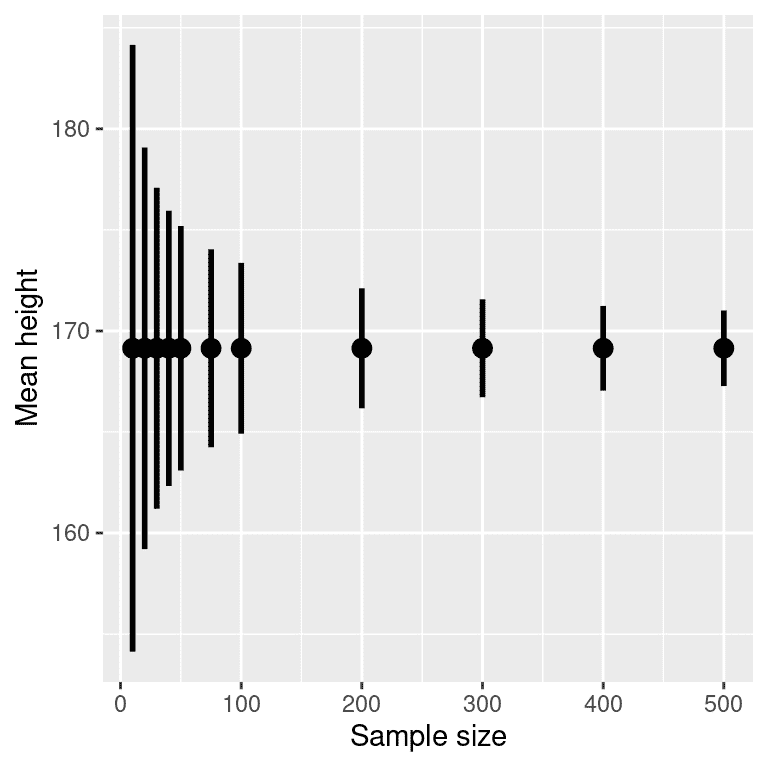
图 10.2：样本量对平均值置信区间宽度的影响的示例。

10.1.4 使用自助法计算置信区间

在某些情况下，我们不能假设正态性，或者我们不知道统计量的抽样分布。在这些情况下，我们可以使用自助法（我们在第[8]章中介绍过）。提醒一下，自助法涉及重复使用有替换的数据进行重新抽样，然后使用在这些样本上计算的统计量的分布作为统计量的抽样分布的替代品。这是我们在 R 中使用内置的自助法函数来计算 NHANES 样本中体重的置信区间的结果：

## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 1000 bootstrap replicates
## 
## CALL : 
## boot.ci(boot.out = bs, type = "perc")
## 
## Intervals : 
## Level     Percentile     
## 95%   (78, 84 )  
## Calculations and Intervals on Original Scale

这些值与上面使用 t 分布获得的值非常接近，尽管不完全相同。

10.1.5 置信区间与假设检验的关系

置信区间与假设检验之间有着密切的关系。特别是，如果置信区间不包括零假设，那么相关的统计检验将具有统计显著性。例如，如果您正在测试样本的平均值是否大于零，$\alpha =0.05$，您可以简单地检查零是否包含在平均值的 95%置信区间内。

如果我们想要比较两个条件的均值（Schenker and Gentleman 2001），事情就会变得更加棘手。有一些情况是明确的。首先，如果每个均值都包含在另一个均值的置信区间内，那么在所选的置信水平下肯定没有显著差异。其次，如果置信区间之间没有重叠，那么在所选的水平上肯定存在显著差异；事实上，这个测试实际上是保守的，这样实际的错误率将低于所选的水平。但是如果置信区间彼此重叠但不包含另一组的均值呢？在这种情况下，答案取决于两个变量的相对变异性，没有通用的答案。然而，一般来说，应该避免使用“目测法”来判断重叠的置信区间。

10.2 效应量

“统计显著性是关于结果最不重要的事情。你应该用量级的度量来描述结果——不仅仅是，治疗是否影响人们，而是它对他们产生了多大影响。” Gene Glass 在(Sullivan and Feinn 2012)中引用。

在前一章中，我们讨论了统计显著性可能并不一定反映实际显著性的想法。为了讨论实际显著性，我们需要一种标准的方式来描述效应的大小，我们称之为效应量。在本节中，我们将介绍这个概念，并讨论计算效应量的各种方法。

效应量是一种标准化的测量，它将某种统计效应的大小与参考数量（如统计的变异性）进行比较。在一些科学和工程领域，这个想法被称为“信噪比”。效应量可以用许多不同的方式来量化，这取决于数据的性质。

10.2.1 Cohen’s D

效应量的最常见测量之一被称为Cohen’s d，以统计学家雅各布·科恩（以他 1994 年的论文“地球是圆的（p < .05）”而闻名）命名。它用于量化两个均值之间的差异，以它们的标准偏差为单位：

$$d=\frac{{\bar{X}}_1?{\bar{X}}_2}{s}$$

${\bar{X}}_1$和${\bar{X}}_2$是两组的均值，$s$是合并标准偏差（这是两个样本的标准偏差的组合，按其样本大小加权）：

$$s=\sqrt{\frac{(n_1?1)s_1^2+(n_2?1)s_2^2}{n_1+n_2?2}}$$

其中$n_1$和$n_2$是样本大小，$s_1^2$和$s_2^2$分别是两组的标准偏差。请注意，这在精神上与 t 统计量非常相似——主要区别在于 t 统计量的分母是基于均值的标准误差，而 Cohen’s D 的分母是基于数据的标准偏差。这意味着随着样本量的增加，t 统计量会增长，而 Cohen’s D 的值将保持不变。

表 10.1：Cohen’s D 的解释

D	解释
0.0 - 0.2	可忽略的
0.2 - 0.5	小
0.5 - 0.8	中等
0.8 -	大

解释效应大小的常用尺度是科恩的 d，如表 10.1 所示。查看一些常见的效应可以帮助理解这些解释是很有用的。例如，成年人身高的性别差异的效应大小（d = 2.05）根据我们上面的表格是非常大的。我们也可以通过查看 NHANES 数据集中样本中男性和女性身高的分布来看到这一点。图 10.3 显示，这两个分布相当分开，但仍有重叠，突出了即使两个群体之间存在非常大的效应大小，仍会有一些个体更像另一群体。

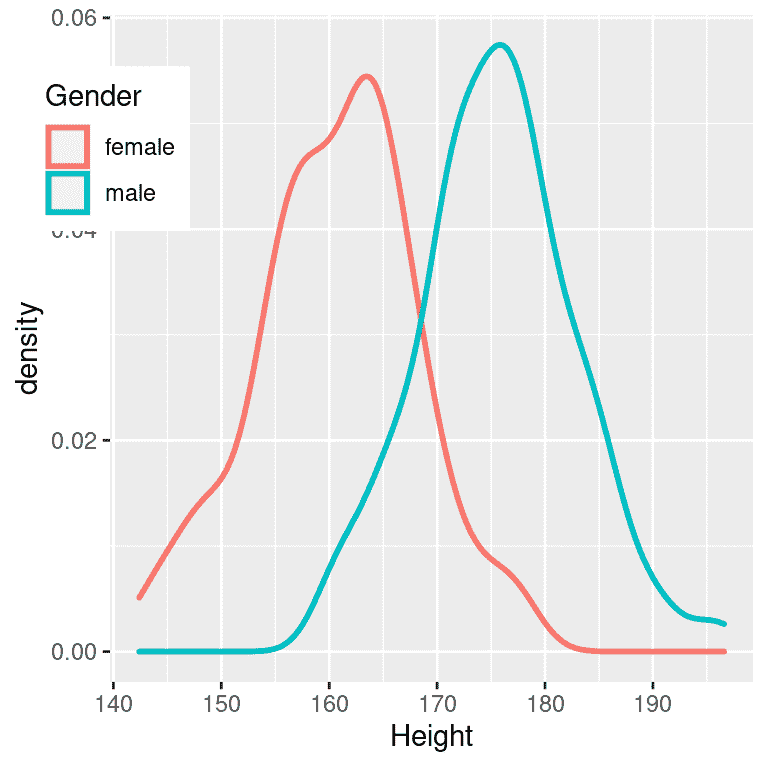
图 10.3: NHANES 数据集中男性和女性身高的平滑直方图，显示出明显不同但也有明显重叠的分布。

值得注意的是，我们在科学中很少遇到这种程度的效应，部分原因是它们是如此明显的效应，我们不需要科学研究来发现它们。正如我们将在第 18 章中看到的，科学研究中报告的非常大的效应往往反映了可疑的研究做法，而不是自然界中真正巨大的效应。值得注意的是，即使对于如此巨大的效应，两个分布仍然有重叠 - 会有一些女性比平均男性更高，反之亦然。对于大多数有趣的科学效应，重叠程度会更大，因此我们不应该立即根据即使是很大的效应大小就对来自不同群体的个体做出强烈的结论。

10.2.2 皮尔逊相关系数 r

皮尔逊r，也称为相关系数，是衡量两个连续变量之间线性关系强度的指标。我们将在第 13 章中更详细地讨论相关性，所以我们将详细内容留到那一章；在这里，我们只是介绍r作为量化两个变量之间关系的一种方式。

r是一个从-1 到 1 变化的度量，其中 1 表示变量之间的完全正相关关系，0 表示没有关系，-1 表示完全负相关关系。图 10.4 使用随机生成的数据显示了不同水平的相关性的示例。

图 10.4: 不同水平的皮尔逊相关系数 r 的示例。

10.2.3 赔率比

在我们之前对概率的讨论中，我们讨论了赔率的概念 - 也就是某个事件发生与不发生的相对可能性：

$$A的赔率=\frac{P(A)}{P(?A)}$$

我们还讨论了赔率比，它只是两个赔率的比率。赔率比是描述二元变量效应大小的一种有用方式。

例如，让我们以吸烟和肺癌为例。2012 年发表在《国际癌症杂志》上的一项研究（Pesch et al. 2012）结合了关于吸烟者和从未吸烟者在许多不同研究中肺癌发生情况的数据。请注意，这些数据来自病例对照研究，这意味着研究参与者之所以被招募，是因为他们有或没有癌症；然后检查了他们的吸烟状况。因此，这些数字（在表 10.2 中显示）并不代表一般人群中吸烟者患癌症的患病率-但它们可以告诉我们癌症和吸烟之间的关系。

表 10.2：吸烟者和从未吸烟者的肺癌发生率分别

状态	从未吸烟	现在吸烟者
无癌症	2883	3829
癌症	220	6784

我们可以将这些数字转换为每个组的几率比。从未吸烟者患肺癌的几率为 0.08，而现在吸烟者患肺癌的几率为 1.77。这些几率的比率告诉我们关于两组之间癌症相对发生率的情况：23.22 的几率比告诉我们吸烟者患肺癌的几率大约是从未吸烟者的 23 倍。

10.3 统计学力量

请记住前一章中提到的，根据 Neyman-Pearson 假设检验方法，我们必须指定我们对两种错误的容忍水平：假阳性（他们称之为第一类错误）和假阴性（他们称之为第二类错误）。人们经常非常关注第一类错误，因为做出假阳性声明通常被视为一件非常糟糕的事情；例如，Wakefield（1999）声称自闭症与疫苗接种有关导致了反疫苗情绪，从而导致麻疹等儿童疾病大幅增加。同样，我们也不想声称一种药物治愈了一种疾病，如果实际上并非如此。这就是为什么对第一类错误的容忍通常设置得相当低，通常为$\alpha =0.05$。但第二类错误呢？

统计学力量的概念是第二类错误的补充-也就是说，它是在存在积极结果的情况下找到积极结果的可能性：

$$力量=1?\beta$$

Neyman-Pearson 模型的另一个重要方面是我们之前没有讨论的，即除了指定可接受的第一类和第二类错误水平外，我们还必须描述一个特定的备择假设-也就是说，我们希望检测的效应大小是多少？否则，我们无法解释$\beta$ - 发现大效应的可能性总是比发现小效应的可能性要高，因此$\beta$将取决于我们试图检测的效应大小。

有三个因素可以影响统计学力量：

• 样本量：较大的样本提供更大的统计学力量

• 效应大小：给定的设计总是比小效应具有更大的功率来发现大效应（因为发现大效应更容易）

• 第一类错误率：第一类错误与力量之间存在关系，即（其他条件相等）降低第一类错误也会降低力量。

我们可以通过模拟来看到这一点。首先让我们模拟一个单一实验，其中我们使用标准 t 检验比较两组的平均值。我们将改变效应大小（以 Cohen 的 d 表示），第一类错误率和样本量，对于每个这些因素，我们将检查显著结果的比例（即力量）如何受到影响。图 10.5 显示了力量如何随这些因素的变化而变化的示例。

图 10.5：来自功率模拟的结果，显示功率作为样本大小的函数，效应大小显示为不同的颜色，α显示为线型。标准的 80%功率标准由虚线黑线表示。

这个模拟告诉我们，即使样本大小为 96，我们也几乎没有足够的功效来发现一个小效应（$d=0.2$），$\alpha =0.005$。这意味着设计这样一个研究将是徒劳的 - 也就是说，即使存在这样大小的真实效应，几乎肯定找不到任何东西。

关于统计功效有至少两个重要的原因。首先，如果你是一名研究人员，你可能不想浪费时间做徒劳的实验。进行功效不足的研究基本上是徒劳的，因为这意味着很低的可能性会发现一个效应，即使它存在。其次，结果表明，与功效充足的研究相比，来自功效不足的研究的任何积极发现更有可能是错误的，这一点我们在第 18 章中会更详细地讨论。

10.3.1 功效分析

幸运的是，有可用的工具可以帮助我们确定实验的统计功效。这些工具最常见的用途是在规划实验时，我们想确定我们的样本需要多大才能有足够的功效来找到我们感兴趣的效应。

假设我们有兴趣进行一项研究，研究 iOS 用户和 Android 用户之间某种个性特征的差异。我们的计划是收集两组个体，并在个性特征上对他们进行测量，然后使用 t 检验比较这两组。在这种情况下，我们认为中等效应（$d=0.5$）是科学上感兴趣的，因此我们将在我们的功效分析中使用这个水平。为了确定必要的样本量，我们可以使用统计软件中的功效函数：

## 
##      Two-sample t test power calculation 
## 
##               n = 64
##           delta = 0.5
##              sd = 1
##       sig.level = 0.05
##           power = 0.8
##     alternative = two.sided
## 
## NOTE: n is number in *each* group

这告诉我们，为了有足够的功效找到中等大小的效应，每组至少需要 64 名受试者。在开始新研究之前进行功效分析总是很重要的，以确保研究不会因为样本太小而徒劳。

你可能会想到，如果效应大小足够大，那么所需的样本将会非常小。例如，如果我们使用 d=2 运行相同的功效分析，那么我们将看到我们只需要每组大约 5 个受试者就足够有能力找到差异。

## 
##      Two-sample t test power calculation 
## 
##               n = 5.1
##               d = 2
##       sig.level = 0.05
##           power = 0.8
##     alternative = two.sided
## 
## NOTE: n is number in *each* group

然而，在科学中很少进行预期发现如此大的效应的实验 - 就像我们不需要统计数据告诉我们 16 岁的人比 6 岁的人更高一样。当我们进行功效分析时，我们需要指定一个对我们的研究来说是合理和/或科学上有趣的效应大小，这通常来自先前的研究。然而，在第 18 章中，我们将讨论一个被称为“赢家诅咒”的现象，这可能导致发表的效应大小比真实效应大小更大，因此这也应该牢记在心中。

10.4 学习目标

阅读完本章后，您应该能够：

• 描述置信区间的正确解释，并计算给定数据集的均值的置信区间。

• 定义效应大小的概念，并计算给定测试的效应大小。

• 描述统计功效的概念以及为什么它对研究很重要。

10.5 建议阅读

• Hoekstra 等人的《置信区间的强偏误解释》

参考资料

Neyman, J. 1937. “Outline of a Theory of Statistical Estimation Based on the Classical Theory of Probability.” Philosophical Transactions of the Royal Society of London A: Mathematical, Physical and Engineering Sciences 236 (767): 333–80. https://doi.org/10.1098/rsta.1937.0005.
Pesch, Beate, Benjamin Kendzia, Per Gustavsson, Karl-Heinz J?ckel, Georg Johnen, Hermann Pohlabeln, Ann Olsson, et al. 2012. “Cigarette Smoking and Lung Cancer–Relative Risk Estimates for the Major Histological Types from a Pooled Analysis of Case-Control Studies.” Int J Cancer 131 (5): 1210–19. https://doi.org/10.1002/ijc.27339.
Schenker, Nathaniel, and Jane F. Gentleman. 2001. “On Judging the Significance of Differences by Examining the Overlap Between Confidence Intervals.” The American Statistician 55 (3): 182–86. http://www.jstor.org/stable/2685796.
Sullivan, Gail M, and Richard Feinn. 2012. “Using Effect Size-or Why the p Value Is Not Enough.” J Grad Med Educ 4 (3): 279–82. https://doi.org/10.4300/JGME-D-12-00156.1.
Wakefield, A J. 1999. “MMR Vaccination and Autism.” Lancet 354 (9182): 949–50. https://doi.org/10.1016/S0140-6736(05)75696-8.

第十一章：贝叶斯统计

原文：statsthinking21.github.io/statsthinking21-core-site/bayesian-statistics.html

译者：飞龙

协议：CC BY-NC-SA 4.0

在本章中，我们将采用与你在第 9 章中遇到的零假设检验框架相对立的统计建模和推断方法。这被称为“贝叶斯统计”，以纪念托马斯·贝叶斯牧师，你在第 6 章已经遇到过他的定理。在本章中，你将学习贝叶斯定理如何提供了一种理解数据的方式，解决了我们讨论的关于零假设检验的许多概念问题，同时也引入了一些新的挑战。

11.1 生成模型

假设你正在走在街上，你的一个朋友就在你身边走过，但没有打招呼。你可能会试图弄清楚为什么会发生这种情况 - 他们没有看到你吗？他们生你的气了吗？你突然被一个魔法隐形盾牌包裹了吗？贝叶斯统计背后的一个基本思想是，我们想根据数据本身推断数据是如何生成的细节。在这种情况下，你想要使用数据（即你的朋友没有打招呼的事实）来推断生成数据的过程（例如他们是否真的看到了你，他们对你的感觉如何等）。

生成模型背后的思想是一个潜在（未见）过程生成我们观察到的数据，通常在过程中有一定的随机性。当我们从一个群体中取样数据并从样本中估计参数时，我们实质上是在试图学习一个潜在变量（群体均值），通过取样产生观察到的数据（样本均值）。图 11.1 显示了这个想法的示意图。

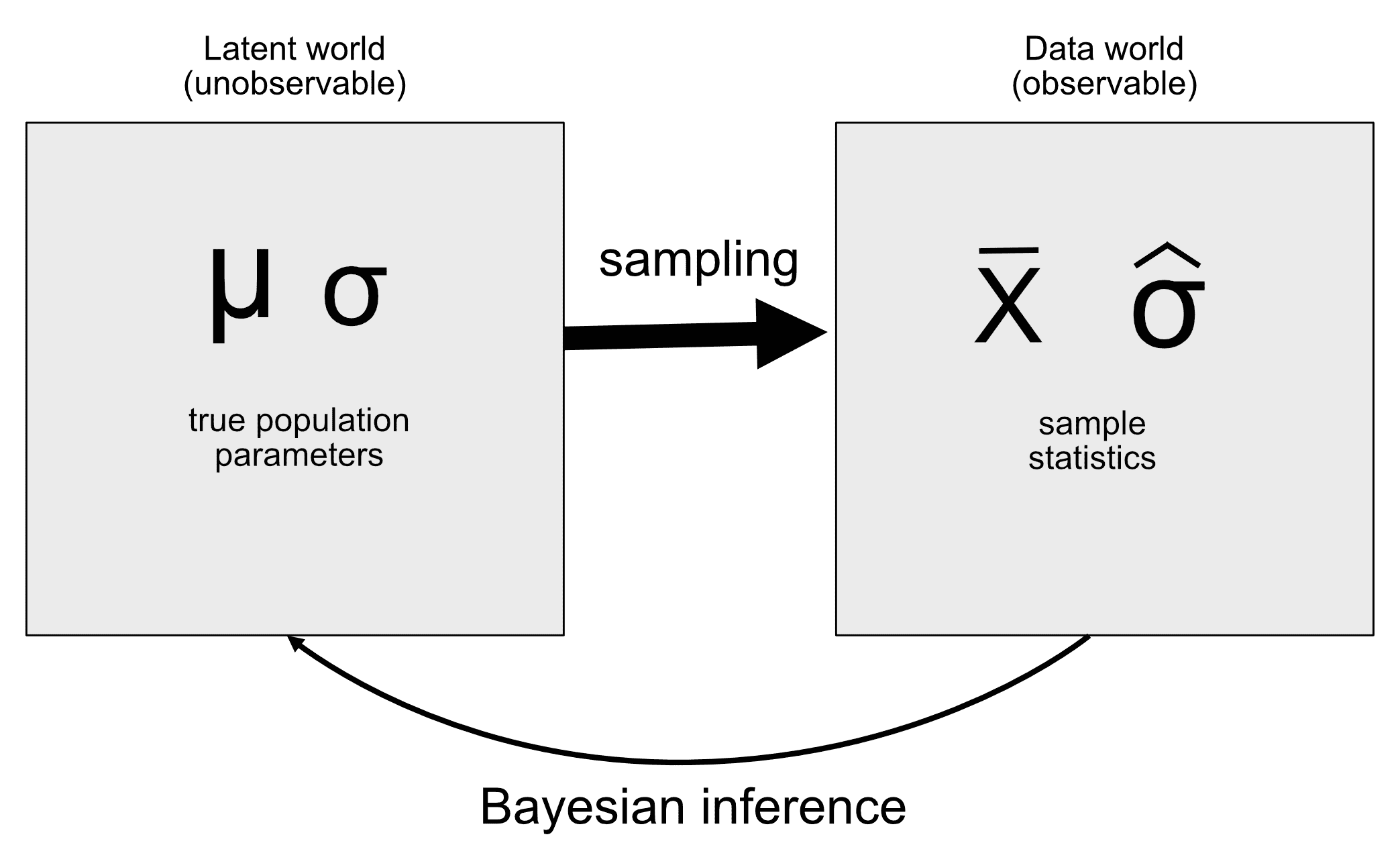
图 11.1：生成模型的想法的示意图。

如果我们知道潜在变量的值，那么重建观察到的数据应该是很容易的。例如，假设我们抛一枚我们知道是公平的硬币，我们期望它 50%的时间会正面朝上。我们可以用二项分布描述硬币，其值为$P_{heads}=0.5$，然后我们可以从这样的分布中生成随机样本，以便看到观察到的数据应该是什么样子。然而，一般情况下我们处于相反的情况：我们不知道感兴趣的潜在变量的值，但我们有一些数据，我们希望用它来估计它。

11.2 贝叶斯定理和逆推推断

贝叶斯统计之所以得名，是因为它利用贝叶斯定理从数据中推断生成数据的潜在过程。假设我们想知道一枚硬币是否公平。为了测试这一点，我们抛了 10 次硬币，得到了 7 次正面。在这个测试之前，我们相当确定$P_{heads}=0.5$，但如果我们相信$P_{heads}=0.5$，那么在 10 次抛硬币中得到 7 次或更多次正面的条件概率（$P(n\ge 7|p_{heads}=0.5)$）会让我们感到犹豫不决。我们已经知道如何使用二项分布计算这个条件概率。

得到的概率是 0.055。这是一个相当小的数字，但这个数字并没有真正回答我们所问的问题 —— 它告诉我们在给定某个特定的正面概率的情况下，出现 7 次或更多正面的可能性，而我们真正想知道的是这枚硬币的真实正面概率。这应该听起来很熟悉，因为这正是我们在零假设检验中遇到的情况，它告诉我们的是数据的可能性而不是假设的可能性。

记住，贝叶斯定理为我们提供了反转条件概率的工具：

$$P(H|D)=\frac{P(D|H)?P(H)}{P(D)}$$

我们可以将这个定理看作有四个部分：

• 先验（$P(假设)$）：在观察到数据 D 之前我们对假设 H 的信念程度

• 似然（$P(数据|假设)$）：在假设 H 下观察到的数据 D 有多大可能性？

• 边际似然（$P(Data)$）：观察到的数据有多大可能性，结合所有可能的假设？

• 后验（$P(假设|数据)$）：在观察到数据 D 后我们对假设 H 的更新信念

在我们抛硬币的例子中：

• 先验（$P_{heads}$）：我们对抛硬币出现正面的可能性的信念程度，即$P_{heads}=0.5$

• 似然（$P(\text{10?次抛硬币中出现?7?次或更多正面}|P_{heads}=0.5)$）：如果$P_{heads}=0.5$，10 次抛硬币中出现 7 次或更多正面的可能性有多大？

• 边际似然（$P(\text{10?次抛硬币中出现?7?次或更多正面}$）：一般情况下，我们观察到 10 次抛硬币中出现 7 次正面的可能性有多大？

• 后验（$P_{heads}|\text{10?次抛硬币中出现?7?次或更多正面}$）：观察到的抛硬币结果后我们对$P_{heads}$的更新信念

在这里，我们看到频率派和贝叶斯统计之间的主要区别之一。频率派不相信有关假设概率的概念（即我们对假设的信念程度） —— 对他们来说，一个假设要么成立要么不成立。另一种说法是，对于频率派来说，假设是固定的，数据是随机的，这就是为什么频率派推断侧重于描述在假设下数据的概率（即 p 值）。另一方面，贝叶斯派则可以舒适地对数据和假设做出概率陈述。

11.3 进行贝叶斯估计

我们最终希望使用贝叶斯统计来对假设做出决策，但在这之前我们需要估计做出决策所需的参数。在这里，我们将介绍贝叶斯估计的过程。让我们再举一个筛查的例子：机场安检。如果你经常飞行，随机的爆炸物筛查结果呈阳性只是时间问题；我在 2001 年 9 月 11 日后不久就经历了这样的不幸经历，当时机场安检人员特别紧张。

安检人员想要知道的是一个人携带爆炸物的可能性，假设机器给出了阳性测试。让我们通过贝叶斯分析来计算这个值。

11.3.1 指定先验

要使用贝叶斯定理，我们首先需要指定假设的先验概率。在这种情况下，我们不知道真实数字，但我们可以假设它相当小。根据FAA的数据，2017 年美国有 971,595,898 名航空乘客。假设其中一名旅客携带了爆炸物 —— 这将给出一个先验概率为 971 百万分之一，非常小！安检人员在 9/11 袭击后的几个月内可能会有更强烈的先验概率，所以我们假设他们的主观信念是每百万名飞行者中有一人携带爆炸物。

11.3.2 收集一些数据

数据由爆炸物筛查测试的结果组成。假设安全人员将袋子通过他们的测试设备进行 3 次测试，并且在 3 次测试中有 3 次阳性读数。

11.3.3 计算可能性

我们想计算在有爆炸物存在的假设下数据的可能性。假设我们知道（来自机器制造商）测试的灵敏度为 0.99 - 也就是说，当设备存在时，它会在 99%的时间内检测到它。为了确定在有设备存在的假设下我们的数据的可能性，我们可以将每个测试视为伯努利试验（即具有真或假结果的试验），成功的概率为 0.99，我们可以使用二项分布来建模。

11.3.4 计算边际可能性

我们还需要知道数据的整体可能性 - 也就是说，在 3 次测试中找到 3 个阳性。计算边际可能性通常是贝叶斯分析中最困难的部分之一，但对于我们的例子来说很简单，因为我们可以利用我们在第[6.7]节中介绍的二元结果的贝叶斯定理的特定形式：

$$P(E|T)=\frac{P(T|E)?P(E)}{P(T|E)?P(E)+P(T|?E)?P(?E)}$$

其中$E$指的是爆炸物的存在，$T$指的是阳性测试结果。

在这种情况下，边际可能性是数据在爆炸物存在或不存在的情况下的可能性的加权平均值，乘以爆炸物存在的概率（即先验）。在这种情况下，假设我们知道（来自制造商）测试的特异性为 0.99，因此当没有爆炸物时的阳性结果的可能性（$P(T|?E)$）为 0.01。

11.3.5 计算后验

现在我们已经有了计算爆炸物存在的后验概率所需的所有部分，这是在观察到 3 次测试中的 3 次阳性结果后。

这个结果告诉我们，在这些阳性测试中，爆炸物在袋子里的后验概率（0.492）略低于 50%，再次突出了测试罕见事件几乎总是容易产生大量假阳性的事实，即使特异性和灵敏度非常高。

贝叶斯分析的一个重要方面是它可以是顺序的。一旦我们有了一个分析的后验，它可以成为下一个分析的先验！

11.4 估计后验分布

在先前的例子中，只有两种可能的结果 - 爆炸物要么存在，要么不存在 - 我们想知道在给定数据的情况下哪种结果最有可能。然而，在其他情况下，我们想使用贝叶斯估计来估计参数的数值。假设我们想了解一种新药物对疼痛的有效性；为了测试这一点，我们可以向一组患者施用药物，然后询问他们在服药后疼痛是否有所改善。我们可以使用贝叶斯分析来估计使用这些数据药物对患者有效的比例。

11.4.1 指定先验

在这种情况下，我们没有关于药物有效性的先验信息，因此我们将使用均匀分布作为我们的先验，因为在均匀分布下所有值都是同等可能的。为了简化例子，我们只会查看 99 个可能有效性值的子集（从.01 到.99，步长为.01）。因此，每个可能的值都有 1/99 的先验概率。

11.4.2 收集一些数据

我们需要一些数据来估计药物的效果。假设我们向 100 个人施用药物，我们发现 64 人对药物有积极反应。

11.4.3 计算可能性

我们可以使用二项密度函数计算在任何特定效果参数值下的观察数据的似然性。在图 11.2 中，您可以看到在几种不同$P_{respond}$值下对响应者数量的似然曲线。从这个图中可以看出，我们的观察数据在$P_{respond}=0.7$的假设下相对更可能，在$P_{respond}=0.5$的假设下略不太可能，在$P_{respond}=0.3$的假设下相当不可能。贝叶斯推断的一个基本思想是，我们应该根据数据在这些值下的可能性来加强我们对感兴趣参数值的信念，同时平衡我们在看到数据之前对参数值的信念（我们的先验知识）。

图 11.2：在几种不同假设下每个可能的响应者数量的似然性（p(respond)=0.5（实线），0.7（虚线），0.3（虚线）。观察值显示在垂直线上

11.4.4 计算边际似然

除了在不同假设下数据的似然性，我们还需要知道数据的整体似然性，结合所有假设（即边际似然）。这种边际似然主要重要是因为它有助于确保后验值是真实概率。在这种情况下，我们使用一组离散可能的参数值使得计算边际似然变得容易，因为我们可以计算每个假设下每个参数值的似然性并将它们相加。

11.4.5 计算后验

我们现在拥有计算后验概率分布的所有部分所需的部分，这些部分涵盖了所有可能的$p_{respond}$值，如图 11.3 所示。

图 11.3：观察数据的后验概率分布以实线绘制，与均匀先验分布（虚线）相对。最大后验概率（MAP）值由菱形符号表示。

11.4.6 最大后验概率（MAP）估计

根据我们的数据，我们想要获得样本的$p_{respond}$估计值。一种方法是找到后验概率最高的$p_{respond}$值，我们称之为最大后验概率（MAP）估计。我们可以从 11.3 的数据中找到这个值——它是在分布顶部标记的值。请注意，结果（0.64）只是我们样本中响应者的比例——这是因为先验是均匀的，因此并没有影响我们的估计。

11.4.7 可信区间

通常，我们不仅想知道后验的单个估计值，还想知道一个区间，我们对后验落在其中有信心。我们之前在频率派推断的背景下讨论了置信区间的概念，您可能还记得置信区间的解释特别复杂：它是一个将包含参数值 95%的时间的区间。我们真正想要的是一个我们对真实参数落在其中有信心的区间，而贝叶斯统计可以给我们这样的区间，我们称之为可信区间。

这个可信区间的解释更接近我们希望从置信区间中得到的（但没有得到）：它告诉我们，有 95%的概率$p_{respond}$的值在这两个数值之间。重要的是，在这种情况下，它表明我们非常有信心$p_{respond}>0.0$，这意味着药物似乎有积极的效果。

在某些情况下，可信区间可以根据已知分布数值计算，但更常见的是通过从后验分布中抽样来生成可信区间，然后计算样本的分位数。当我们没有简单的方法来数值表达后验分布时，这种方法特别有用，而在真实的贝叶斯数据分析中通常是这种情况。这样的一种方法（拒绝抽样）在本章末尾的附录中有更详细的解释。

11.4.8 不同先验的影响

在前面的例子中，我们使用了平坦先验，这意味着我们没有理由相信$p_{respond}$的任何特定值更可能或更不可能。然而，假设我们之前有一些先前的数据：在一项先前的研究中，研究人员测试了 20 人，发现其中有 10 人对治疗作出了积极反应。这将导致我们开始具有先验信念，即治疗对 50%的人有效。我们可以做与上面相同的计算，但使用我们先前研究的信息来指导我们的先验（参见图 11.4 的 A 面板）。

请注意，似然和边际似然没有改变 - 只有先验改变了。先验变化的效果是将后验拉近到新先验的集中点，即 0.5。

现在让我们看看如果我们带着更强烈的先验信念进行分析会发生什么。假设我们之前观察到 20 个人中有 10 个反应者，而先前的研究测试了 500 人，发现 250 个反应者。这原则上应该给我们一个更强的先验，正如我们在图 11.4 的 B 面板中看到的那样：先验更加集中在 0.5 附近，后验也更接近先验。总的想法是，贝叶斯推断结合了先验和似然的信息，权衡了每个的相对强度。

这个例子也突出了贝叶斯分析的顺序性质 - 一个分析的后验可以成为下一个分析的先验。

最后，重要的是要意识到，如果先验足够强大，它们可以完全压倒数据。假设你有一个绝对先验，即$p_{respond}$大于等于 0.8，这样你就将所有其他值的先验概率设为零。如果我们计算后验会发生什么呢？

图 11.4：A：先验对后验分布的影响。基于平坦先验的原始后验分布以蓝色绘制。基于 20 人中 10 名回答者的观察的先验以虚线黑色线绘制，使用此先验的后验以红色绘制。B：先验强度对后验分布的影响。蓝线显示使用基于 100 人中 50 个头的先验获得的后验。虚线黑线显示基于 500 次抛硬币中 250 个头的先验，红线显示基于该先验的后验。C：先验强度对后验分布的影响。蓝线显示使用绝对先验获得的后验，该先验表明 p（回答）为 0.8 或更高。先验以虚线黑线显示。

在图 11.4 的 C 面板中，我们看到后验中没有任何值的密度，其中先验被设为零 - 数据被绝对先验所压倒。

11.5 选择先验

贝叶斯统计中最具争议的方面是先验对推断结果的影响。什么是正确的先验？如果先验的选择决定了结果（即后验），你如何确信你的结果是可信的？这些是困难的问题，但我们不应该因为面对困难问题而退缩。正如我们之前讨论过的，贝叶斯分析给我们提供了可解释的结果（可信区间等）。这本身就应该激励我们认真思考这些问题，以便得出合理和可解释的结果。

有各种方法可以选择先验，这些方法（如上所述）可能会影响结果的推断。有时我们有一个非常具体的先验，就像我们预期硬币掷出正面的概率为 50%一样，但在许多情况下，我们没有这样强烈的起点。无信息先验试图尽可能少地影响结果的后验，就像我们在上面的均匀先验的例子中看到的那样。使用弱信息先验（或默认先验）也很常见，它们只会轻微地影响结果。例如，如果我们使用基于两次抛硬币中的一次正面的二项分布，先验将以 0.5 为中心，但相当平坦，只会轻微地影响后验。还可以使用基于科学文献或现有数据的先验，我们称之为经验先验。然而，总的来说，我们将坚持使用无信息/弱信息先验，因为它们最少地引起我们对结果的担忧。

11.6 贝叶斯假设检验

学会了如何进行贝叶斯估计后，我们现在转向使用贝叶斯方法进行假设检验。假设有两位政治家在他们对公众是否支持额外税收以支持国家公园的信念上存在差异。史密斯参议员认为只有 40%的人支持这项税收，而琼斯参议员认为有 60%的人支持。他们安排进行一项民意调查来测试这一点，询问了 1000 名随机选取的人是否支持这样的税收。结果是，在接受调查的样本中，有 490 人支持这项税收。基于这些数据，我们想知道：数据是否支持一位参议员的主张胜过另一位，以及胜过多少？我们可以使用一个称为贝叶斯因子的概念来测试这一点，它通过比较每个假设对观察到的数据的预测能力来量化哪个假设更好。

11.6.1 贝叶斯因子

贝叶斯因子表征了数据在两种不同假设下的相对可能性。它的定义如下：

$$BF=\frac{p(data|H_1)}{p(data|H_2)}$$

对于两个假设$H_1$和$H_2$。在我们的两位参议员的情况下，我们知道如何使用二项分布计算每个假设下数据的可能性；暂时假设每位参议员的先验概率相同（$P_{H_1}=P_{H_2}=0.5$）。我们将参议员史密斯放在分子中，参议员琼斯放在分母中，这样大于一的值将反映对参议员史密斯更大的证据，小于一的值将反映对参议员琼斯更大的证据。得到的贝叶斯因子（3325.26）提供了关于数据支持两个假设的证据的度量 - 在这种情况下，它告诉我们数据支持参议员史密斯比支持参议员琼斯强大 3000 多倍。

11.6.2 统计假设的贝叶斯因子

在前面的例子中，我们对每位参议员都有具体的预测，我们可以使用二项分布来量化它们的可能性。此外，我们对两个假设的先验概率是相等的。然而，在实际数据分析中，我们通常必须处理关于参数的不确定性，这使得贝叶斯因子变得复杂，因为我们需要计算边际似然（即在所有可能的模型参数上的似然的综合平均，按其先验概率加权）。然而，作为交换，我们获得了量化支持零假设与备择假设相对证据量的能力。

假设我们是一名进行糖尿病治疗临床试验的医学研究人员，我们希望知道一种特定药物是否与安慰剂相比能够降低血糖。我们招募了一组志愿者，并将他们随机分配到药物组或安慰剂组，然后我们测量在药物或安慰剂使用期间每组的血红蛋白 A1C（血糖水平的标志）的变化。我们想知道的是：药物和安慰剂之间是否有差异？

首先，让我们生成一些数据并使用零假设检验进行分析（参见图 11.5）。然后让我们进行独立样本 t 检验，结果显示组之间存在显著差异：

图 11.5：箱线图显示药物组和安慰剂组的数据。

## 
##  Welch Two Sample t-test
## 
## data:  hbchange by group
## t = 2, df = 32, p-value = 0.02
## alternative hypothesis: true difference in means between group 0 and group 1 is greater than 0
## 95 percent confidence interval:
##  0.11  Inf
## sample estimates:
## mean in group 0 mean in group 1 
##          -0.082          -0.650

这个检验告诉我们组之间存在显著差异，但它并没有量化证据支持零假设与备择假设的强度。为了衡量这一点，我们可以使用 R 中 BayesFactor 包的ttestBF函数计算贝叶斯因子：

## Bayes factor analysis
## --------------
## [1] Alt., r=0.707 0<d<Inf    : 3.4  ±0%
## [2] Alt., r=0.707 !(0<d<Inf) : 0.12 ±0.01%
## 
## Against denominator:
##   Null, mu1-mu2 = 0 
## ---
## Bayes factor type: BFindepSample, JZS

我们特别关注大于零效应的贝叶斯因子，在报告中标有“[1]”的行中列出。这里的贝叶斯因子告诉我们，备择假设（即差异大于零）相对于点零假设（即均值差异恰好为零）在数据给定的情况下大约有 3 倍的可能性。因此，虽然效应是显著的，但它提供给我们支持备择假设的证据量相当弱。

11.6.2.1 单侧检验

我们通常对特定点值的零假设（例如，平均差异= 0）进行测试的兴趣不如对方向性零假设（例如，差异小于或等于零）进行测试。我们还可以使用ttestBF分析的结果执行方向（或单侧）检验，因为它提供两个贝叶斯因子：一个是备择假设，即平均差异大于零，另一个是备择假设，即平均差异小于零。如果我们想评估正效应的相对证据，我们可以通过简单地将函数返回的两个贝叶斯因子相除来计算比较正效应与负效应的相对证据：

## Bayes factor analysis
## --------------
## [1] Alt., r=0.707 0<d<Inf : 29 ±0.01%
## 
## Against denominator:
##   Alternative, r = 0.707106781186548, mu =/= 0 !(0<d<Inf) 
## ---
## Bayes factor type: BFindepSample, JZS

现在我们看到，正效应与负效应的贝叶斯因子大得多（几乎 30）。

11.6.2.2 解释贝叶斯因子

我们如何知道贝叶斯因子为 2 或 20 是好还是坏？Kass & Rafferty (1995)提出了贝叶斯因子解释的一般指导方针：

BF	证据的强度
1 到 3	不值一提
3 到 20	正效应
20 到 150	强
>150	非常强

基于此，即使统计结果显着，支持备择假设与点零假设相比的证据量也很弱，几乎不值一提，而对于方向性假设的证据相对较强。

11.6.3 评估零假设的证据

因为贝叶斯因子比较了两个假设的证据，所以它还允许我们评估是否有证据支持零假设，这是标准零假设检验无法做到的（因为它假设零假设为真）。这对于确定非显著结果是否真的提供了无效果的强有力证据，或者只是总体证据较弱非常有用。

11.7 学习目标

阅读完本章后，应该能够：

• 描述贝叶斯分析和零假设检验之间的主要区别

• 描述并执行贝叶斯分析的步骤

• 描述不同先验的影响以及选择先验的考虑因素

• 描述置信区间和贝叶斯可信区间之间的解释差异

11.8 建议阅读

• 《不会消失的理论：贝叶斯定理如何破译了密码，追踪俄罗斯潜艇，并在两个世纪的争议中胜出》，作者：沙龙·伯奇·麦格雷恩

• 《贝叶斯数据分析：R 的教程介绍》，作者：约翰·K·克鲁斯克

11.9 附录：

11.9.1 拒绝抽样

我们将使用一种称为拒绝抽样的简单算法从后验分布中生成样本。其思想是我们从均匀分布中选择 x（在本例中为$p_{respond}$）和 y（在本例中为$p_{respond}$的后验概率）的随机值。然后，我们只接受样本，如果$y<f(x)$ - 在本例中，如果随机选择的 y 值小于 y 的实际后验概率。图 11.6 显示了使用拒绝抽样的样本直方图示例，以及使用该方法获得的 95％可信区间（表??中的值）。

	x
2.5%	0.54
97.5%	0.73

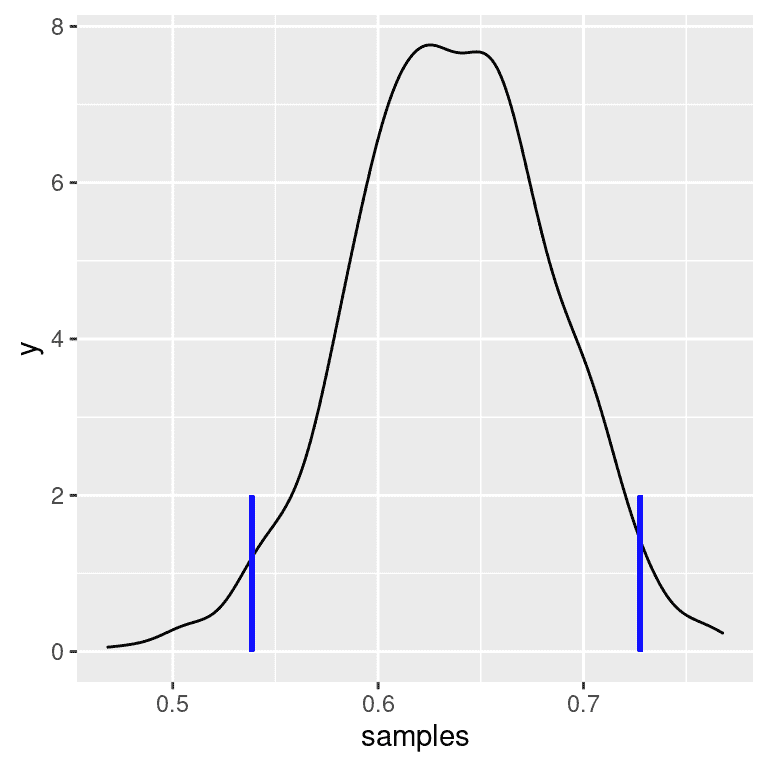
图 11.6：拒绝抽样示例。黑线显示了 p(回答)所有可能值的密度；蓝线显示了分布的 2.5 和 97.5 百分位数，代表了对 p(回答)估计的 95%可信区间。

第十二章：建模分类关系

原文：statsthinking21.github.io/statsthinking21-core-site/modeling-categorical-relationships.html

译者：飞龙

协议：CC BY-NC-SA 4.0

到目前为止，我们已经讨论了统计建模和假设检验的一般概念，并将它们应用于一些简单的分析；现在我们将转向如何在我们的数据中建模特定类型的关系的问题。在本章中，我们将重点关注分类关系的建模，这意味着我们测量的变量之间的关系是定性的。这些数据通常用计数来表示；也就是说，对于变量的每个值（或多个变量的组合的值），有多少观察值取该值？例如，当我们统计我们班上每个专业的人数时，我们正在对数据进行分类建模。

12.1 示例：糖果颜色

假设我购买了一袋 100 颗糖果，标有 1/3 巧克力、1/3 甘露和 1/3 甘露的标签。当我数袋子里的糖果时，我们得到以下数字：30 颗巧克力，33 颗甘露和 37 颗甘露。因为我比甘露或甘露更喜欢巧克力，我觉得有点被欺骗，我想知道这是否只是一个偶然事件。为了回答这个问题，我需要知道：如果每种糖果的真实概率是平均比例的 1/3，那么计数出现这种情况的可能性是多少？

12.2 皮尔逊卡方检验

Pearson 卡方检验为我们提供了一种测试一组观察计数是否与定义零假设的特定期望值不同的方法：

$${\chi }^2=\sum _i\frac{(observe{d}_i?expecte{d}_i{)}^2}{expecte{d}_i}$$

在我们糖果的例子中，零假设是每种类型的糖果的比例相等。要计算卡方统计量，我们首先需要在零假设下得出我们的期望计数：因为零假设是它们都相同，那么这只是在三个类别之间分割的总计数（如表 12.1 所示）。然后我们取每个计数与其在零假设下的期望值之间的差异，对它们进行平方，除以零假设，然后将它们相加以获得卡方统计量。

表 12.1：糖果数据中的观察计数、零假设下的期望值和平方差

糖果类型	计数	零假设	平方差
巧克力	30	33	11.11
甘露	33	33	0.11
口香糖	37	33	13.44

这个分析的卡方统计量为 0.74，单独来看是无法解释的，因为它取决于被加在一起的不同值的数量。然而，我们可以利用卡方统计量在零假设下分布的事实，这被称为卡方分布。该分布被定义为一组标准正态随机变量的平方和；它的自由度数量等于被加在一起的变量的数量。分布的形状取决于自由度的数量。图 12.1 的左面板显示了几个不同自由度的分布示例。

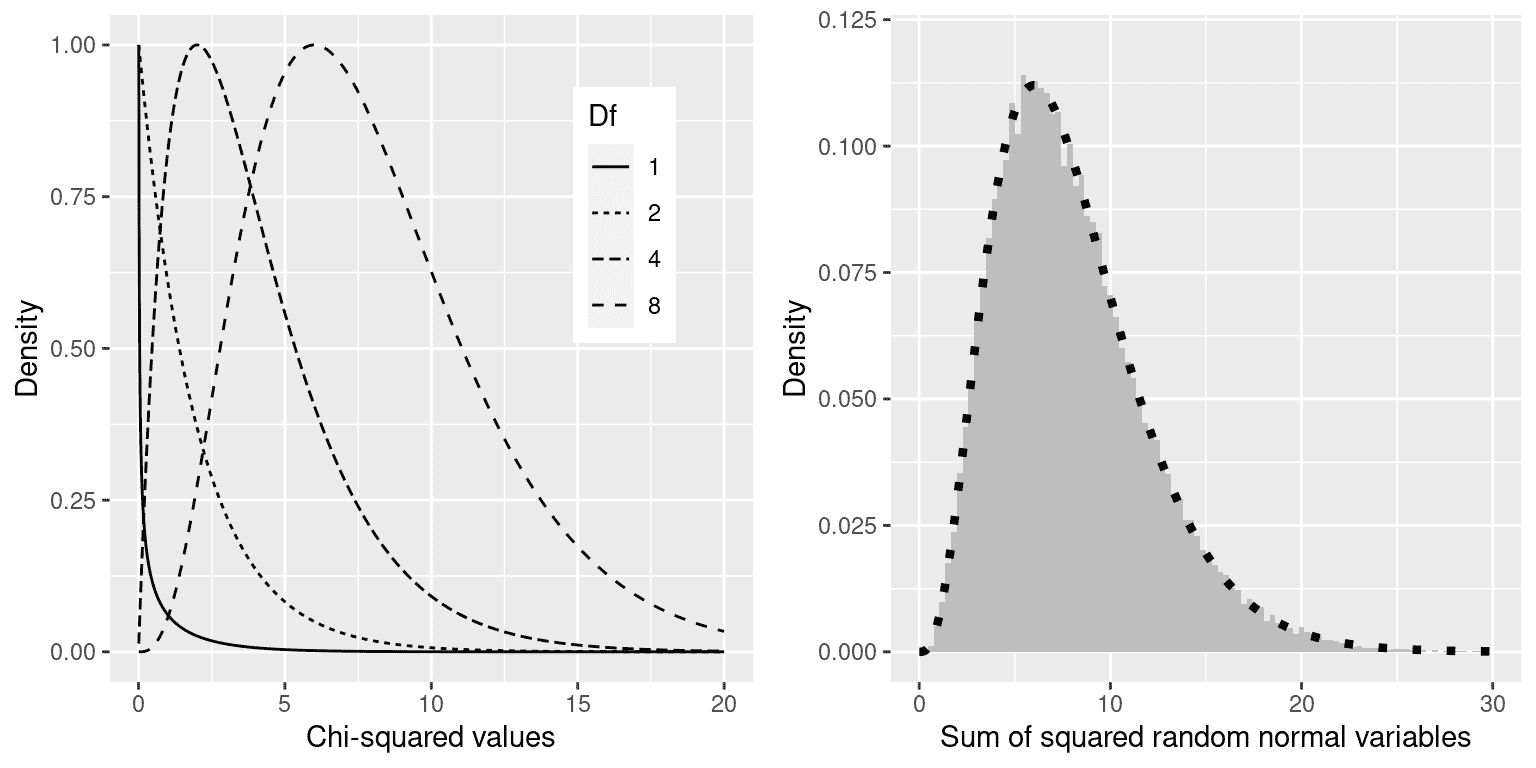
图 12.1：左：不同自由度下卡方分布的示例。右：随机正态变量平方和的模拟。直方图基于 50,000 组 8 个随机正态变量的平方和；虚线显示了具有 8 个自由度的理论卡方分布的值。

让我们通过模拟验证卡方分布是否准确描述了一组标准正态随机变量的平方和，为此，我们反复抽取 8 个随机数，并在平方每个值后将每组相加。图 12.1 的右面板显示，理论分布与重复添加一组随机正态变量的平方的模拟结果非常接近。

对于糖果的例子，我们可以计算在所有糖果上频率相等的零假设下观察到的卡方值 0.74 的可能性。我们使用自由度等于 k - 1 的卡方分布（其中 k = 类别数），因为当我们计算均值以生成期望值时，我们失去了一个自由度。得到的 p 值（P(Chi-squared) > 0.74 = 0.691）显示，根据糖果袋上印刷的比例，观察到的糖果数量并不特别令人惊讶，我们不会拒绝等比例的零假设。

12.3 列联表和双向检验

我们经常使用卡方检验的另一种方式是询问两个分类变量是否彼此相关。作为更现实的例子，让我们来看看一个问题，即当警察拦下一名司机时，黑人司机是否比白人司机更有可能被搜查。斯坦福开放警务项目(openpolicing.stanford.edu/)对此进行了研究，并提供了我们可以用来分析这个问题的数据。我们将使用康涅狄格州的数据，因为它们相对较小，因此更容易分析。

用列联表来表示分类分析数据的标准方法，它展示了每个变量可能组合的观察数量或比例。下面的表 12.2 显示了警察搜查数据的列联表。使用比例而不是原始数字来查看列联表也是有用的，因为它们在视觉上更容易比较，因此我们在这里包括了绝对和相对数字。

表 12.2：警察搜查数据的列联表

被搜查	黑	白	黑（相关）	白（相关）
FALSE	36244	239241	0.13	0.86
TRUE	1219	3108	0.00	0.01

皮尔逊卡方检验允许我们测试观察频率是否与期望频率不同，因此我们需要确定如果搜查和种族无关，即我们可以定义为独立，则每个单元格中我们期望的频率是什么。请记住，从概率章节中可以知道，如果 X 和 Y 是独立的，那么：

$$P(X\cap Y)=P(X)?P(Y)$$

也就是说，在独立性的零假设下，联合概率简单地是每个单独变量的边际概率的乘积。边际概率只是每个事件发生的概率，而不考虑其他事件。我们可以计算这些边际概率，然后将它们相乘以得到独立性下的期望比例。

	黑色	白色
没被搜查	P(NS)*P(B)	P(NS)*P(W)	P(NS)
被搜查	P(S)*P(B)	P(S)*P(W)	P(S)
	P(B)	P(W)

然后我们计算卡方统计量，结果为 828.3。为了计算 p 值，我们需要将其与零假设下的卡方分布进行比较，以确定我们的卡方值与零假设下的预期相比有多极端。这个分布的自由度是$df=(nRows?1)?(nColumns?1)$ - 因此，对于像这里的 2X2 表，$df=(2?1)?(2?1)=1$。直觉在于计算期望频率需要我们使用三个值：观察总数和两个变量的边际概率。因此，一旦这些值被计算出来，就只有一个数字可以自由变化，因此只有一个自由度。鉴于此，我们可以计算卡方统计量的 p 值，这个 p 值接近于零：$3.79\times 10^{?182}$。这表明如果种族和警察搜查真的没有关系，观察到的数据将是非常不可能的，因此我们应该拒绝独立性的零假设。

我们也可以使用我们的统计软件轻松进行这个测试。

## 
##  Pearson's Chi-squared test
## 
## data:  summaryDf2wayTable and 1
## X-squared = 828, df = 1, p-value <2e-16

12.4 标准化残差

当我们在卡方检验中发现显著效应时，这告诉我们数据在零假设下不太可能发生，但它并不告诉我们数据有何不同。为了更深入地了解数据与零假设下的预期有何不同，我们可以检查模型的残差，这反映了数据（即观察频率）与模型（即期望频率）在每个单元格中的偏差。与查看原始残差（这将仅根据数据中的观察次数而变化）不同，更常见的是查看标准化残差（有时称为皮尔逊残差），计算公式如下：

$$标准化残{差}_{ij}=\frac{观{察}_{ij}?期{望}_{ij}}{\sqrt{期{望}_{ij}}}$$

其中$i$和$j$分别是行和列的索引。

表 12.3 显示了警察停车数据的标准化残差。这些标准化残差可以解释为 Z 分数 - 在这种情况下，我们看到黑人被搜查的次数远远高于独立性预期，而白人被搜查的次数远远低于预期。这为我们提供了解释显著卡方结果所需的背景。

表 12.3：警察停车数据的标准化残差总结

搜查	驾驶员种族	标准化残差
FALSE	黑人	-3.3
TRUE	黑人	26.6
FALSE	白人	1.3
TRUE	白人	-10.4

12.5 赔率比

我们还可以使用我们之前介绍的赔率比来表示列联表中不同结果的相对可能性，以更好地理解效应的大小。首先，我们表示每个种族被停车的赔率，然后计算它们的比率：

$$赔{率}_{黑人被搜查}=\frac{N_{黑人被搜查}}{N_{黑人未被搜查}}=\frac{1219}{36244}=0.034$$

$$赔{率}_{白人被搜查}=\frac{N_{白人被搜查}}{N_{白人未被搜查}}=\frac{3108}{239241}=0.013$$

$$赔率比=\frac{赔{率}_{黑人被搜查}}{赔{率}_{白人被搜查}}=2.59$$

赔率比显示，根据这个数据集，黑人被搜查的赔率是白人的 2.59 倍。

12.6 贝叶斯因子

我们在之前关于贝叶斯统计的章节中讨论了贝叶斯因子 - 你可能还记得它代表了数据在两个假设下的可能性比：

$$K=\frac{P(data|H_A)}{P(data|H_0)}=\frac{P(H_A|data)?P(H_A)}{P(H_0|data)?P(H_0)}$$

我们可以使用我们的统计软件计算警察搜查数据的贝叶斯因子：

## Bayes factor analysis
## --------------
## [1] Non-indep. (a=1) : 1.8e+142 ±0%
## 
## Against denominator:
##   Null, independence, a = 1 
## ---
## Bayes factor type: BFcontingencyTable, independent multinomial

这表明在这个数据集中，关于驾驶员种族和警察搜查之间关系的证据非常强大——$1.8?10^{142}$接近无穷大，这在统计学中是我们能想象到的最接近无穷大的了。

12.7 超过 2X2 表的分类分析

分类分析也可以应用于列联表，其中每个变量有两个以上的类别。

例如，让我们看看 NHANES 数据，并比较变量Depressed，它表示“参与者感到沮丧、抑郁或绝望的天数”。这个变量编码为None、Several或Most。让我们测试一下这个变量是否与SleepTrouble变量相关，后者表示个体是否向医生报告了睡眠问题。

12.4 表：NHANES 数据集中抑郁和睡眠问题之间的关系

抑郁	无睡眠问题	有睡眠问题
None	2614	676
Several	418	249
Most	138	145

仅仅通过观察这些数据，我们就可以得知这两个变量之间可能存在关系；值得注意的是，尽管有睡眠问题的人数远少于没有睡眠问题的人数，但对于报告大部分时间感到抑郁的人来说，有睡眠问题的人数大于没有睡眠问题的人数。我们可以直接使用卡方检验来量化这一点：

## 
##  Pearson's Chi-squared test
## 
## data:  depressedSleepTroubleTable
## X-squared = 191, df = 2, p-value <2e-16

这个检验表明抑郁和睡眠问题之间存在着强烈的关系。我们还可以计算贝叶斯因子来量化支持备择假设的证据的强度：

## Bayes factor analysis
## --------------
## [1] Non-indep. (a=1) : 1.8e+35 ±0%
## 
## Against denominator:
##   Null, independence, a = 1 
## ---
## Bayes factor type: BFcontingencyTable, joint multinomial

在这里，我们看到贝叶斯因子非常大（$1.8?10^{35}$），表明抑郁和睡眠问题之间的关系证据非常强大。

12.8 小心辛普森悖论

上面呈现的列联表代表了大量观察结果的总结，但总结有时可能会产生误导。让我们以棒球为例。下表显示了 1995-1997 年间 Derek Jeter 和 David Justice 的击球数据（安打/打数和击球平均率）：

运动员	1995		1996		1997		合并后
Derek Jeter	12/48	.250	183/582	.314	190/654	.291	385/1284	.300
David Justice	104/411	.253	45/140	.321	163/495	.329	312/1046	.298

如果你仔细观察，你会发现有些奇怪的事情发生了：在每个单独的年份里，贾斯蒂斯的击球平均率都高于杰特，但当我们将所有三年的数据合并时，杰特的平均率实际上高于贾斯蒂斯的！这是辛普森悖论的一个例子，即在合并数据集中存在的模式可能在数据子集中不存在。这是因为在不同的子集中可能有另一个变量在变化——在这种情况下，打数在不同年份中变化，贾斯蒂斯在 1995 年击球次数更多（当时击球平均率较低）。我们称之为潜在变量，在检验分类数据时，始终要注意这些变量是非常重要的。

12.9 学习目标

• 描述分类数据的列联表概念。

• 描述卡方检验的关联概念，并为给定的列联表计算它。

• 描述辛普森悖论及其对分类数据分析的重要性。

12.10 额外阅读

• 心理科学中的辛普森悖论：实用指南

第十三章：建模连续关系

原文：statsthinking21.github.io/statsthinking21-core-site/modeling-continuous-relationships.html

译者：飞龙

协议：CC BY-NC-SA 4.0

大多数人都熟悉相关性的概念，在本章中，我们将对这个常用且常被误解的概念提供更正式的理解。

13.1 例子：仇恨犯罪和收入不平等

2017 年，网站 Fivethirtyeight.com 发表了一篇名为Higher Rates Of Hate Crimes Are Tied To Income Inequality的故事，讨论了 2016 年总统选举后仇恨犯罪的流行程度与收入不平等之间的关系。该故事报道了来自 FBI 和南方贫困法律中心的仇恨犯罪数据的分析，根据这些数据，他们报道：

“我们发现收入不平等是美国各地人口调整后的仇恨犯罪和仇恨事件的最重要决定因素”。

这项分析的数据可作为 R 统计软件的fivethirtyeight包的一部分获得，这使我们可以轻松访问它们。故事中报告的分析侧重于收入不平等（由一种称为基尼指数的数量定义——有关更多细节，请参见附录）与每个州仇恨犯罪的流行程度之间的关系。

13.2 收入不平等与仇恨犯罪有关吗？

图 13.1：仇恨犯罪率与基尼指数的图表。

收入不平等与仇恨犯罪率之间的关系显示在图 13.1 中。从数据来看，似乎这两个变量之间可能存在正相关关系。我们如何量化这种关系呢？

13.3 协方差和相关性

量化两个变量之间关系的一种方法是协方差。记住，单个变量的方差是每个数据点与均值之间的平方差的平均值：

$$s^2=\frac{{\sum }_{i=1}^n(x_i?\bar{x}{)}^2}{N?1}$$

这告诉我们每个观察值平均而言与均值的距离是多少的平方单位。协方差告诉我们观察中两个不同变量的偏差之间是否存在关系。它的定义是：

$$covariance=\frac{{\sum }_{i=1}^n(x_i?\bar{x})(y_i?\bar{y})}{N?1}$$

当个体数据点以相似的方式偏离各自的均值时，这个值将远离零；如果它们以相同的方向偏离，协方差是正的，而如果它们以相反的方向偏离，协方差是负的。让我们先看一个玩具示例。数据如表 13.1 所示，以及它们与均值的个体偏差和它们的交叉乘积。

表 13.1：协方差玩具示例的数据

x	y	y_dev	x_dev	交叉乘积
3	5	-3.6	-4.6	16.56
5	4	-4.6	-2.6	11.96
8	7	-1.6	0.4	-0.64
10	10	1.4	2.4	3.36
12	17	8.4	4.4	36.96

协方差简单地是交叉乘积的平均值，在这种情况下是 17.05。我们通常不使用协方差来描述变量之间的关系，因为它随着数据中方差的整体水平而变化。相反，我们通常会使用相关系数（通常在统计学家卡尔·皮尔逊之后称为皮尔逊相关系数）。相关性是通过将协方差按两个变量的标准差进行缩放来计算的。

$$r=\frac{covariance}{s_x{s}_y}=\frac{{\sum }_{i=1}^n(x_i?\bar{x})(y_i?\bar{y})}{(N?1)s_x{s}_y}$$

在这种情况下，该值为 0.89。相关系数很有用，因为它在数据的性质不同的情况下都在-1 和 1 之间变化 - 实际上，我们在讨论效应大小时已经讨论过相关系数。正如我们在上一章中看到的，相关系数为 1 表示完美的线性关系，相关系数为-1 表示完美的负相关关系，相关系数为零表示没有线性关系。

13.3.1 相关性的假设检验

仇恨犯罪和收入不平等之间的相关值为 0.42，似乎表明两者之间有相当强的关系，但我们也可以想象即使没有关系，这种情况也可能发生。我们可以使用一个简单的方程来测试相关性是否为零，这个方程可以将相关值转换为t统计量：

$${\text{t}}_r=\frac{r\sqrt{N?2}}{\sqrt{1?r^2}}$$

在零假设$H_0:r=0$下，这个统计量服从自由度为$N?2$的 t 分布。我们可以使用我们的统计软件来计算这个值：

## 
##  Pearson's product-moment correlation
## 
## data:  hateCrimes$avg_hatecrimes_per_100k_fbi and hateCrimes$gini_index
## t = 3, df = 48, p-value = 0.002
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.16 0.63
## sample estimates:
##  cor 
## 0.42

这个检验表明在零假设下，出现这么极端或更极端的 r 值的可能性是相当低的，所以我们会拒绝$r=0$的零假设。请注意，这个检验假设两个变量都是正态分布的。

我们也可以通过随机化来测试这一点，即我们反复洗牌其中一个变量的值并计算相关性，然后将我们观察到的相关值与这个零分布进行比较，以确定在零假设下我们观察到的值有多大可能性。结果显示在图 13.2 中。使用随机化计算的 p 值与 t 检验给出的答案相当相似。

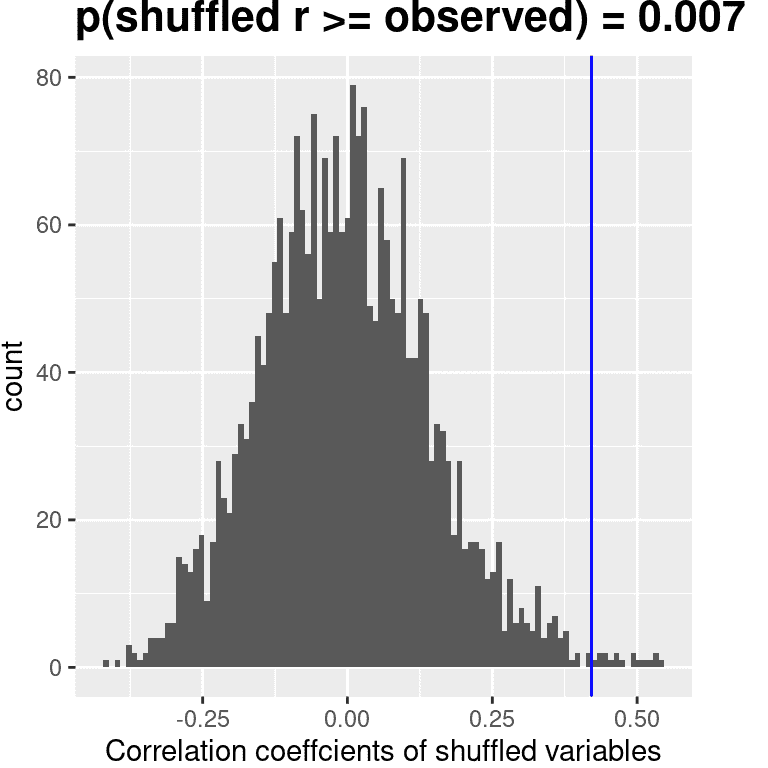
图 13.2: 在零假设下相关值的直方图，通过洗牌值获得。观察值由蓝线表示。

我们也可以使用贝叶斯推断来估计相关性；更多信息请参见附录。

13.3.2 鲁棒相关性

你可能已经注意到在图 13.1 中有一些奇怪的地方 - 其中一个数据点（哥伦比亚特区的数据点）似乎与其他数据点相当分离。我们称之为离群值，标准相关系数对离群值非常敏感。例如，在图 13.3 中，我们可以看到一个离群数据点会导致一个非常高的正相关值，即使其他数据点之间的实际关系是完全负相关的。

图 13.3: 离群值对相关性的影响的模拟示例。没有离群值，其余数据点具有完美的负相关关系，但单个离群值将相关值改变为高度正相关。

解决异常值的一种方法是对数据进行排序后计算秩相关性，而不是对数据本身进行计算；这被称为Spearman 相关性。在图 13.3 的示例中，皮尔逊相关性为 0.83，而 Spearman 相关性为-0.45，显示秩相关性减少了异常值的影响，并反映了大多数数据点之间的负相关关系。

我们也可以对仇恨犯罪数据进行秩相关性计算：

## 
##  Spearman's rank correlation rho
## 
## data:  hateCrimes$avg_hatecrimes_per_100k_fbi and hateCrimes$gini_index
## S = 20146, p-value = 0.8
## alternative hypothesis: true rho is not equal to 0
## sample estimates:
##   rho 
## 0.033

现在我们看到相关性不再显著（实际上非常接近零），这表明 FiveThirtyEight 博客文章的说法可能是错误的，因为异常值的影响。

13.4 相关性和因果关系

当我们说一件事导致另一件事时，我们是什么意思？哲学上长期存在关于因果关系含义的讨论，但在统计学中，我们通常认为因果关系的一种方式是通过实验控制来思考。也就是说，如果我们认为因素 X 导致因素 Y，那么操纵 X 的值也应该改变 Y 的值。

在医学上，有一套被称为柯赫氏假说的观念，它们历来被用来确定特定生物是否导致疾病。基本思想是，该生物应该存在于患有疾病的人体内，而在没有疾病的人体内不存在——因此，消除该生物的治疗也应该消除疾病。此外，感染该生物应该导致患者患上疾病。马歇尔博士的工作中就有一个例子，他假设胃溃疡是由一种细菌（幽门螺杆菌）引起的。为了证明这一点，他用这种细菌感染了自己，不久之后他的胃就严重发炎了。然后他用抗生素治疗自己，他的胃很快就恢复了。后来他因这项工作获得了诺贝尔医学奖。

通常我们想要测试因果假设，但实际上我们无法进行实验，要么是因为不可能（“人类碳排放与地球气候之间的关系是什么？”），要么是不道德的（“严重虐待对儿童大脑发育的影响是什么？”）。然而，我们仍然可以收集可能与这些问题相关的数据。例如，我们可以潜在地收集受虐待儿童和未受虐待儿童的数据，然后问他们的大脑发育是否不同。

假设我们进行了这样的分析，并发现受虐待的儿童的大脑发育不如未受虐待的儿童。这是否证明虐待导致大脑发育不良？不。每当我们观察到两个变量之间的统计关联时，其中一个变量导致另一个变量是完全可能的。但也有可能两个变量都受到第三个变量的影响；在这个例子中，可能是儿童虐待与家庭压力相关，家庭压力也可能通过较少的智力参与、食物压力或其他可能的途径导致大脑发育不良。关键是，两个变量之间的相关性通常告诉我们某件事可能导致另一件事，但它并没有告诉我们是什么导致了什么。

13.4.1 因果图

描述变量之间因果关系的一种有用方法是通过因果图，它将变量显示为圆圈，变量之间的因果关系显示为箭头。例如，图 13.4 显示了学习时间和我们认为应受其影响的两个变量之间的因果关系：考试成绩和考试完成时间。

然而，实际上，完成时间和成绩的影响并不是直接由学习时间决定的，而是由学生通过学习获得的知识量决定的。我们通常会说知识是一个潜在变量 - 也就是说，我们无法直接测量它，但我们可以通过我们可以测量的变量（比如成绩和完成时间）来看到它的反映。图 13.5 展示了这一点。

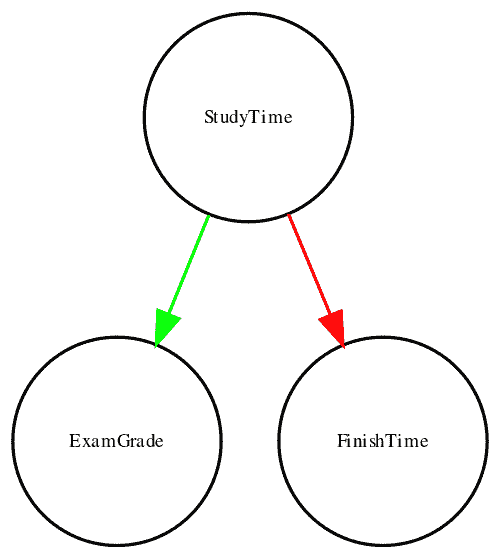
图 13.4：一个图表显示了三个变量之间的因果关系：学习时间、考试成绩和考试完成时间。绿色箭头代表正相关关系（即更多的学习时间导致考试成绩提高），红色箭头代表负相关关系（即更多的学习时间导致考试完成时间更快）。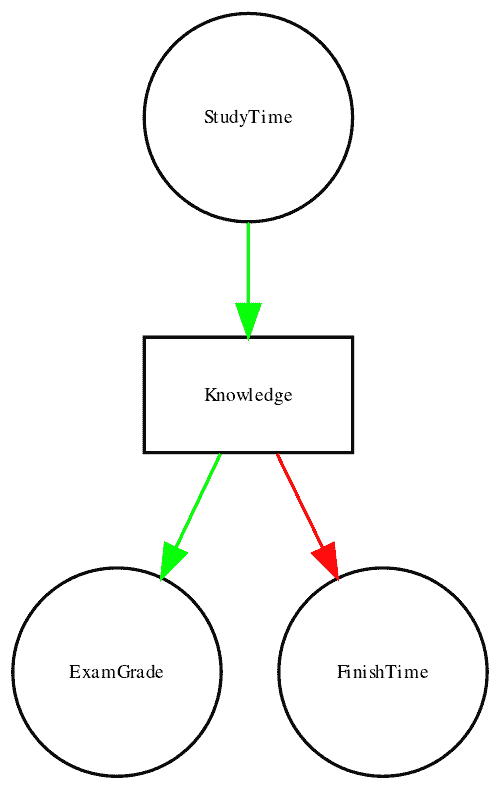

图 13.5：一个图表显示了与上文相同的因果关系，但现在还显示了潜在变量（知识）使用一个方框来表示。

在这里，我们会说知识中介了学习时间和成绩/完成时间之间的关系。这意味着如果我们能够保持知识恒定（例如，通过给药物导致立即遗忘），那么学习时间就不应该再对成绩和完成时间产生影响了。

请注意，如果我们只是测量考试成绩和完成时间，我们通常会看到它们之间存在负相关关系，因为通常情况下，完成考试最快的人得到的成绩最高。然而，如果我们将这种相关性解释为因果关系，这将告诉我们为了获得更好的成绩，我们实际上应该更快地完成考试！这个例子展示了从非实验数据中推断因果关系有多么棘手。

统计学和机器学习领域有一个非常活跃的研究社区，目前正在研究如何从非实验数据中推断因果关系的问题。然而，这些方法通常需要做出强烈的假设，并且必须谨慎使用。

13.5 学习目标

阅读完本章后，您应该能够：

• 描述相关系数的概念及其解释

• 计算两个连续变量之间的相关性

• 描述异常数据点的影响以及如何处理它们。

• 描述可能导致观察到的相关性的潜在因果影响。

13.6 建议阅读

• Judea Pearl 的《为什么》（http://bayes.cs.ucla.edu/WHY/）- 一个关于因果推断背后思想的优秀介绍。

13.7 附录：

13.7.1 量化不平等：基尼系数

在我们看报道中的分析之前，首先了解基尼系数如何用来量化不平等是很有用的。基尼系数通常是用收入和收入低于或等于该水平的人口比例之间的关系来定义的，称为洛伦兹曲线。然而，另一种更直观的思考方式是：它是收入之间的相对平均绝对差异，除以二（来自en.wikipedia.org/wiki/Gini_coefficient）：

$$G=\frac{\sum _{i=1}^n\sum _{j=1}^n\left|x_i?x_j\right|}{2n\sum _{i=1}^n{x}_i}$$

图 13.6：A）完全平等，B）正态分布收入和 C）高度不平等（除了一个非常富有的个人外，收入相等）的洛伦兹曲线。

图 13.6 显示了几种不同收入分布的洛伦兹曲线。左上面板（A）显示了一个有 10 个人的例子，每个人的收入完全相同。点之间的间隔长度相等，表明每个人在总人口收入中赚取了相同的份额。右上面板（B）显示了一个收入正态分布的例子。左下面板显示了一个高度不平等的例子；每个人的收入都相等（40,000 美元），除了一个人，他的收入是 40,000,000 美元。根据美国人口普查，2010 年美国的基尼系数为 0.469，大致处于我们正态分布和最不平等的例子之间。

13.7.2 贝叶斯相关分析

我们还可以使用贝叶斯分析来分析 FiveThirtyEight 数据，这有两个优点。首先，它为我们提供了后验概率 - 在这种情况下，相关值超过零的概率。其次，贝叶斯估计结合了观察到的证据和先验，这使得正则化相关估计，有效地将其拉向零。在这里，我们可以使用 R 中的BayesFactor包来计算它。

## Bayes factor analysis
## --------------
## [1] Alt., r=0.333 : 21 ±0%
## 
## Against denominator:
##   Null, rho = 0 
## ---
## Bayes factor type: BFcorrelation, Jeffreys-beta*

## Summary of Posterior Distribution
## 
## Parameter | Median |       95% CI |     pd |          ROPE | % in ROPE |    BF |         Prior
## ----------------------------------------------------------------------------------------------
## rho       |   0.38 | [0.13, 0.58] | 99.88% | [-0.05, 0.05] |        0% | 20.85 | Beta (3 +- 3)

请注意，使用贝叶斯方法估计的相关性（0.38）略小于使用标准相关系数估计的相关性（0.42），这是因为估计是基于证据和先验的组合，有效地将估计值收缩到零。然而，请注意，贝叶斯分析对异常值不具有鲁棒性，它仍然表明有相当强的证据表明相关性大于零（贝叶斯因子超过 20）。

第十四章：通用线性模型

原文：statsthinking21.github.io/statsthinking21-core-site/the-general-linear-model.html

译者：飞龙

协议：CC BY-NC-SA 4.0

请记住，在本书的早期，我们描述了统计学的基本模型：

$$数据=模型+误差$$，我们的一般目标是找到最小化误差的模型，同时满足其他一些约束（例如保持模型相对简单，以便我们可以推广到我们的特定数据集之外）。在本章中，我们将专注于这种方法的特定实现，即通用线性模型（或 GLM）。在早期关于将模型拟合到数据的章节中，您已经看到了通用线性模型，我们对 NHANES 数据集中的身高建模为年龄的函数；在这里，我们将更一般地介绍 GLM 的概念及其许多用途。几乎统计学中使用的每个模型都可以用通用线性模型或其扩展来表述。

在讨论通用线性模型之前，让我们首先定义两个对我们讨论重要的术语：

• 因变量：这是我们的模型旨在解释的结果变量（通常称为Y）

• 自变量：这是我们希望用来解释因变量的变量（通常称为X）。

可能会有多个自变量，但在本课程中，我们将主要关注分析中只有一个因变量的情况。

通用线性模型是一个模型，其中因变量的模型由独立变量的线性组合组成，每个独立变量都乘以一个权重（通常称为希腊字母 beta - $\beta$），这决定了该独立变量对模型预测的相对贡献。

图 14.1：学习时间和成绩之间的关系

举个例子，让我们生成一些模拟数据，来描述学习时间和考试成绩之间的关系（见图 14.1）。根据这些数据，我们可能想要进行统计学的三个基本活动：

• 描述：成绩和学习时间之间的关系有多强？

• 决定：成绩和学习时间之间是否存在统计学上显著的关系？

• 预测：给定特定的学习时间，我们期望得到什么成绩？

在上一章中，我们学习了如何使用相关系数描述两个变量之间的关系。让我们使用统计软件来计算这些数据的相关关系，并测试相关性是否显著不同于零：

## 
##  Pearson's product-moment correlation
## 
## data:  df$grade and df$studyTime
## t = 2, df = 6, p-value = 0.09
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  -0.13  0.93
## sample estimates:
##  cor 
## 0.63

相关性非常高，但请注意，估计周围的置信区间非常宽，几乎涵盖了从零到一的整个范围，这在一定程度上是由于样本量较小造成的。

14.1 线性回归

我们可以使用通用线性模型来描述两个变量之间的关系，并决定该关系是否具有统计学意义；此外，该模型还允许我们根据自变量的新值来预测因变量的值。最重要的是，通用线性模型将允许我们构建包含多个自变量的模型，而相关系数只能描述两个单独变量之间的关系。

我们用于此的 GLM 的具体版本被称为线性回归。 回归一词是由弗朗西斯·高尔顿创造的，他注意到当他比较父母和他们的孩子在某些特征上（如身高）时，极端父母的孩子（即非常高或非常矮的父母）通常比他们的父母更接近平均值。这是一个非常重要的观点，我们将在下面回到这一点。

线性回归模型的最简单版本（具有单个自变量）可以表示如下：

$$y=x?{\beta }_x+{\beta }_0+?$$ ${\beta }_x$值告诉我们，我们期望 y 在给定 x 变化一个单位时会发生多大变化。截距${\beta }_0$是一个整体偏移量，告诉我们当$x=0$时我们期望 y 有什么值；您可能还记得我们早期建模讨论中提到的，即使$x$从未真正达到零，这对于模拟数据的整体幅度也很重要。误差项$?$指的是模型拟合后剩下的东西；我们经常将这些称为模型的残差。如果我们想知道在估计了$\beta$值之后如何预测 y（我们称之为$\hat{y}$），那么我们可以去掉误差项：

$$\hat{y}=x?\widehat{{\beta }_x}+\widehat{{\beta }_0}$$

请注意，这只是一条线的方程，其中$\widehat{{\beta }_x}$是我们对斜率的估计，$\widehat{{\beta }_0}$是截距。图 14.2 显示了将此模型应用于研究时间数据的示例。

图 14.2：研究时间数据的线性回归解决方案显示在实线中，截距的值等于当 x 变量等于零时 y 变量的预测值；这用虚线表示。 beta 的值等于线的斜率-也就是说，y 在 x 变化一个单位时的变化量。这在虚线中以示意图的方式显示，显示了学习时间增加一个单位时成绩的增加程度。

我们不会详细介绍如何从数据中实际估计最佳拟合斜率和截距；如果您感兴趣，可以在附录中找到详细信息。

14.1.1 回归到平均值

回归到平均值的概念是高尔顿对科学的重要贡献之一，当我们解释实验数据分析的结果时，这仍然是一个关键点。假设我们想研究阅读干预对差阅读者表现的影响。为了测试我们的假设，我们可能会进入学校并招募那些在某项阅读测试的分布中处于最低 25%的个体，进行干预，然后检查他们在干预后的测试中的表现。假设干预实际上没有效果，这样每个个体的阅读分数只是来自正态分布的独立样本。这个假设实验的计算机模拟结果在表 14.1 中呈现。

表 14.1：测试 1 的阅读分数（较低，因为它是选择学生的基础）和测试 2 的阅读分数（较高，因为它与测试 1 无关）。

	分数
测试 1	88
测试 2	101

如果我们看一下第一次和第二次测试的平均测试表现之间的差异，似乎干预帮助了这些学生，因为他们的分数在测试中提高了超过十分！然而，我们知道实际上学生们并没有改善，因为在这两种情况下，分数只是从随机正态分布中随机选择的。发生的是一些学生在第一次测试中由于随机机会而表现不佳。如果我们仅基于他们的第一次测试成绩选择这些学科，他们肯定会在第二次测试中回到整个组的平均水平，即使培训没有任何效果。这就是为什么我们总是需要一个未经处理的对照组来解释由于干预而导致的任何性能变化；否则我们很可能会被回归到平均值所欺骗。此外，参与者需要被随机分配到对照组或治疗组，这样两组之间就不会有任何系统性差异（平均而言）。

14.1.2 相关和回归之间的关系

相关系数和回归系数之间有着密切的关系。记住 Pearson 相关系数是由 x 和 y 的协方差和标准差的乘积的比值计算得出的：

$$\hat{r}=\frac{covarianc{e}_{xy}}{s_x?s_y}$$

而 x 的回归 beta 计算如下：

$$\widehat{{\beta }_x}=\frac{covarianc{e}_{xy}}{s_x?s_x}$$

基于这两个方程，我们可以推导出$\hat{r}$和$\widehat{beta}$之间的关系：

$$covarianc{e}_{xy}=\hat{r}?s_x?s_y$$

$$\widehat{{\beta }_x}=\frac{\hat{r}?s_x?s_y}{s_x?s_x}=r?\frac{s_y}{s_x}$$

也就是说，回归斜率等于相关值乘以 y 和 x 的标准差的比值。这告诉我们的一件事是，当 x 和 y 的标准差相同时（例如当数据已转换为 Z 分数时），相关估计等于回归斜率估计。

14.1.3 回归模型的标准误差

如果我们想对回归参数估计进行推断，那么我们还需要估计它们的变异性。为了计算这一点，我们首先需要计算模型的残差方差或误差方差——也就是，因变量中有多少变异性不是由模型解释的。我们可以计算模型残差如下：

$$residual=y?\hat{y}=y?(x?\widehat{{\beta }_x}+\widehat{{\beta }_0})$$

然后我们计算平方误差和（SSE）：

$$S{S}_{error}=\sum _{i=1}^n(y_i?\widehat{y_i}{)}^2=\sum _{i=1}^{n}residual{s}^2$$

然后我们计算均方误差：

$$M{S}_{error}=\frac{S{S}_{error}}{df}=\frac{{\sum }_{i=1}^n(y_i?\widehat{y_i}{)}^2}{N?p}$$

其中自由度（$df$）由观测数（$N$）减去估计参数数（在这种情况下为 2：$\widehat{{\beta }_x}$和$\widehat{{\beta }_0}$）确定。一旦我们有了均方误差，我们就可以计算模型的标准误差。

$$S{E}_{model}=\sqrt{M{S}_{error}}$$

为了获得特定回归参数估计的标准误差$S{E}_{{\beta }_x}$，我们需要通过 X 变量的平方和的平方根重新调整模型的标准误差：

$$S{E}_{{\hat{\beta }}_x}=\frac{S{E}_{model}}{\sqrt{\sum (x_i?\bar{x}{)}^2}}$$

14.1.4 回归参数的统计检验

一旦我们有了参数估计和它们的标准误差，我们就可以计算一个t统计量，告诉我们观察到的参数估计与零假设下的某个期望值相比的可能性。在这种情况下，我们将针对没有效果的零假设进行检验（即$\beta =0$）：

$$\begin{array}{c}{t}_{N?p}=\frac{\hat{\beta }?{\beta }_{expected}}{S{E}_{\hat{\beta }}}\\ t_{N?p}=\frac{\hat{\beta }?0}{S{E}_{\hat{\beta }}}\\ t_{N?p}=\frac{\hat{\beta }}{S{E}_{\hat{\beta }}}\end{array}$$

一般来说，我们会使用统计软件来计算这些值，而不是手工计算。以下是 R 中线性模型函数的结果：

## 
## Call:
## lm(formula = grade ~ studyTime, data = df)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -10.656  -2.719   0.125   4.703   7.469 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    76.16       5.16   14.76  6.1e-06 ***
## studyTime       4.31       2.14    2.01    0.091 .  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 6.4 on 6 degrees of freedom
## Multiple R-squared:  0.403,  Adjusted R-squared:  0.304 
## F-statistic: 4.05 on 1 and 6 DF,  p-value: 0.0907

在这种情况下，我们看到截距与零显著不同（这并不是很有趣），而 studyTime 对成绩的影响略显显著（p = .09）- 与我们之前进行的相关性检验相同的 p 值。

14.1.5 量化模型的拟合优度

有时候量化模型整体拟合数据的好坏是很有用的，其中一种方法是询问模型能解释数据变异性的多少。这可以用一个叫做$R^2$的值来量化（也被称为决定系数）。如果只有一个 x 变量，那么可以通过简单地平方相关系数来计算：

$$R^2=r^2$$

在我们的学习时间示例中，$R^2$ = 0.4，这意味着我们解释了大约 40%的成绩方差。

更一般地，我们可以将$R^2$看作是模型解释数据方差的比例，可以通过将方差分解为多个部分来计算：

这很令人困惑，改为残差而不是误差

$$S{S}_{total}=S{S}_{model}+S{S}_{error}$$

其中$S{S}_{total}$是数据（$y$）的方差，$S{S}_{model}$和$S{S}_{error}$如本章前面所示计算。有了这些，我们可以计算决定系数：

$$R^2=\frac{S{S}_{model}}{S{S}_{total}}=1?\frac{S{S}_{error}}{S{S}_{total}}$$

一个小的$R^2$值告诉我们，即使模型拟合在统计上是显著的，它可能只解释了数据中的一小部分信息。

14.2 拟合更复杂的模型

通常我们希望了解多个变量对某个特定结果的影响，以及它们之间的关系。在我们的学习时间示例中，假设我们发现一些学生之前曾上过相关课程。如果我们绘制他们的成绩（见图 14.3），我们可以看到那些之前上过课程的学生在相同的学习时间下表现得比那些没有上过课程的学生要好得多。我们希望建立一个统计模型来考虑这一点，我们可以通过扩展上面建立的模型来实现：

$$\hat{y}=\widehat{{\beta }_1}?studyTime+\widehat{{\beta }_2}?priorClass+\widehat{{\beta }_0}$$

为了模拟每个个体是否之前上过课程，我们使用所谓的虚拟编码，其中我们创建一个新变量，其值为 1 表示之前上过课程，否则为 0。这意味着对于之前上过课程的人，我们将简单地将$\widehat{{\beta }_2}$的值添加到他们的预测值中-也就是说，使用虚拟编码，$\widehat{{\beta }_2}$反映了两组之间的均值差异。我们对$\widehat{{\beta }_1}$的估计反映了所有数据点的回归斜率-我们假设回归斜率在某人之前是否上过课程的情况下是相同的（见图 14.3）。

## 
## Call:
## lm(formula = grade ~ studyTime + priorClass, data = df)
## 
## Residuals:
##       1       2       3       4       5       6       7       8 
##  3.5833  0.7500 -3.5833 -0.0833  0.7500 -6.4167  2.0833  2.9167 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    70.08       3.77   18.60  8.3e-06 ***
## studyTime       5.00       1.37    3.66    0.015 *  
## priorClass1     9.17       2.88    3.18    0.024 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 4 on 5 degrees of freedom
## Multiple R-squared:  0.803,  Adjusted R-squared:  0.724 
## F-statistic: 10.2 on 2 and 5 DF,  p-value: 0.0173

图 14.3：包括先前经验作为模型中的附加组件的学习时间和成绩之间的关系。实线将学习时间与没有先前经验的学生的成绩联系起来，虚线将成绩与具有先前经验的学生的学习时间联系起来。点线对应于两组之间的平均差异。

14.3 变量之间的交互作用

在先前的模型中，我们假设学习时间对成绩的影响（即回归斜率）对两组是相同的。然而，在某些情况下，我们可能会想象一个变量的影响可能会根据另一个变量的值而有所不同，我们称之为变量之间的交互作用。

让我们使用一个新的例子来提出问题：咖啡因对公开演讲有什么影响？首先让我们生成一些数据并绘制它们。从图 14.4 的 A 面来看，似乎没有关系，我们可以通过对数据进行线性回归来确认这一点。

## 
## Call:
## lm(formula = speaking ~ caffeine, data = df)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -33.10 -16.02   5.01  16.45  26.98 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)
## (Intercept)   -7.413      9.165   -0.81     0.43
## caffeine       0.168      0.151    1.11     0.28
## 
## Residual standard error: 19 on 18 degrees of freedom
## Multiple R-squared:  0.0642, Adjusted R-squared:  0.0122 
## F-statistic: 1.23 on 1 and 18 DF,  p-value: 0.281

但现在假设我们发现研究表明焦虑和非焦虑的人对咖啡因有不同的反应。首先让我们分别为焦虑和非焦虑的人绘制数据。

从图 14.4 的 B 面可以看出，似乎演讲和咖啡因之间的关系对两组是不同的，咖啡因可以提高没有焦虑的人的表现，但会降低有焦虑的人的表现。我们想要创建一个可以回答这个问题的统计模型。首先让我们看看如果我们只在模型中包括焦虑会发生什么。

## 
## Call:
## lm(formula = speaking ~ caffeine + anxiety, data = df)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -32.97  -9.74   1.35  10.53  25.36 
## 
## Coefficients:
##                   Estimate Std. Error t value Pr(>|t|)
## (Intercept)        -12.581      9.197   -1.37     0.19
## caffeine             0.131      0.145    0.91     0.38
## anxietynotAnxious   14.233      8.232    1.73     0.10
## 
## Residual standard error: 18 on 17 degrees of freedom
## Multiple R-squared:  0.204,  Adjusted R-squared:  0.11 
## F-statistic: 2.18 on 2 and 17 DF,  p-value: 0.144

在这里我们看到咖啡因和焦虑都没有显著的影响，这可能有点令人困惑。问题在于这个模型试图使用相同的斜率来关联演讲和咖啡因对两组。如果我们想要使用具有不同斜率的线来拟合它们，我们需要在模型中包括交互作用，这相当于为两组中的每一组拟合不同的线；这通常用在模型中使用$*)符号来表示。

## 
## Call:
## lm(formula = speaking ~ caffeine + anxiety + caffeine * anxiety, 
##     data = df)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -11.385  -7.103  -0.444   6.171  13.458 
## 
## Coefficients:
##                            Estimate Std. Error t value Pr(>|t|)    
## (Intercept)                 17.4308     5.4301    3.21  0.00546 ** 
## caffeine                    -0.4742     0.0966   -4.91  0.00016 ***
## anxietynotAnxious          -43.4487     7.7914   -5.58  4.2e-05 ***
## caffeine:anxietynotAnxious   1.0839     0.1293    8.38  3.0e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 8.1 on 16 degrees of freedom
## Multiple R-squared:  0.852,  Adjusted R-squared:  0.825 
## F-statistic: 30.8 on 3 and 16 DF,  p-value: 7.01e-07

从这些结果中，我们看到咖啡因和焦虑都有显著的影响（我们称之为主效应），以及咖啡因和焦虑之间的交互作用。图 14.4 的 C 面显示了每组的分开回归线。

图 14.4：A：咖啡因和公开演讲之间的关系。B：咖啡因和公开演讲之间的关系，焦虑由数据点的形状表示。C：公开演讲和咖啡因之间的关系，包括与焦虑的交互作用。这导致了两条分别为每组建模的线（对焦虑的虚线，对非焦虑的点线）。

一个重要的要点是，如果存在显著的交互作用，我们必须非常小心地解释显著的主效应，因为交互作用表明主效应根据另一个变量的值而不同，因此不容易解释。

有时我们想要比较两个不同模型的相对拟合，以确定哪个是更好的模型；我们称之为模型比较。对于上面的模型，我们可以使用所谓的方差分析来比较具有交互作用和不具有交互作用的模型的拟合度：

## Analysis of Variance Table
## 
## Model 1: speaking ~ caffeine + anxiety
## Model 2: speaking ~ caffeine + anxiety + caffeine * anxiety
##   Res.Df  RSS Df Sum of Sq    F Pr(>F)    
## 1     17 5639                             
## 2     16 1046  1      4593 70.3  3e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

这告诉我们有很好的证据表明，更喜欢具有交互作用的模型而不是没有交互作用的模型。在这种情况下，模型比较相对简单，因为这两个模型是嵌套的 - 其中一个模型是另一个模型的简化版本，简化模型中的所有变量都包含在更复杂的模型中。与非嵌套模型的模型比较可能会变得更加复杂。

14.4 超越线性预测和结果

重要的是要注意，尽管它被称为一般线性模型，我们实际上可以使用相同的方法来建模不遵循直线的效应（如曲线）。一般线性模型中的“线性”并不是指响应的形状，而是指模型在其参数上是线性的 - 也就是说，模型中的预测变量只与参数相乘，而不是像被提高到参数的幂这样的非线性关系。分析的数据通常是二元的而不是连续的，正如我们在分类结果的章节中所看到的那样。有一些方法可以调整一般线性模型（称为广义线性模型），允许进行这种类型的分析。我们将在本书的后面探讨这些模型。

14.5 批评我们的模型和检查假设

“垃圾进，垃圾出”这句话在统计学中同样适用。在统计模型的情况下，我们必须确保我们的模型被正确指定，并且我们的数据适合模型。

当我们说模型“被正确指定”时，我们的意思是我们已经在模型中包含了适当的自变量集。我们已经看到了错误指定模型的例子，在图 5.3 中。请记住，我们看到了几种情况，模型未能正确解释数据，比如未包括截距。在构建模型时，我们需要确保它包括所有适当的变量。

我们还需要担心我们的模型是否满足我们统计方法的假设。当使用一般线性模型时，我们做出的最重要的假设之一是残差（即模型预测与实际数据之间的差异）是正态分布的。这可能会因为模型未正确指定或者我们建模的数据不合适而失败。

我们可以使用称为Q-Q（分位数-分位数）图来查看我们的残差是否服从正态分布。您已经遇到过分位数 - 它们是截断特定累积分布的比例值。Q-Q 图将两个分布的分位数相互对比；在这种情况下，我们将实际数据的分位数与同一数据拟合的正态分布的分位数进行对比。图 14.5 显示了两个这样的 Q-Q 图的示例。左侧面板显示了来自正态分布的数据的 Q-Q 图，而右侧面板显示了来自非正态数据的 Q-Q 图。右侧面板中的数据点与线明显偏离，反映了它们不是正态分布的事实。

qq_df <- tibble(norm=rnorm(100),
 unif=runif(100))

p1 <- ggplot(qq_df,aes(sample=norm)) + 
 geom_qq() + 
 geom_qq_line() + 
 ggtitle('Normal data')

p2 <- ggplot(qq_df,aes(sample=unif)) + 
 geom_qq() + 
 geom_qq_line()+ 
 ggtitle('Non-normal data')

plot_grid(p1,p2)

图 14.5：正态（左）和非正态（右）数据的 Q-Q 图。线显示了 x 轴和 y 轴相等的点。

模型诊断将在后面的章节中更详细地探讨。

14.6 “预测”真正意味着什么？

当我们在日常生活中谈论“预测”时，我们通常指的是在看到数据之前估计某个变量的值的能力。然而，在线性回归的背景下，这个术语通常用来指代将模型拟合到数据；估计的值（$\hat{y}$）有时被称为“预测”，而独立变量被称为“预测变量”。这有一个不幸的含义，因为它意味着我们的模型也应该能够预测未来新数据点的值。实际上，将模型拟合到用于获取参数的数据集的拟合几乎总是比将模型拟合到新数据集的拟合要好（Copas 1983）。

例如，让我们从 NHANES 中抽取 48 个儿童的样本，并为包括几个回归器（年龄、身高、看电视和使用电脑的小时数以及家庭收入）及其交互作用的体重拟合回归模型。

表 14.2：应用于原始数据和新数据的模型的均方根误差，以及在对 y 变量的顺序进行洗牌后的结果（实质上使零假设成立）

数据类型	RMSE（原始数据）	RMSE（新数据）
真实数据	3.0	25
洗牌数据	7.8	59

在这里，我们看到，尽管在原始数据上拟合的模型显示出非常好的拟合（每个个体只有几公斤的偏差），但对于从同一人群中抽样的新儿童的体重值，同样的模型预测效果要差得多（每个个体超过 25 公斤的偏差）。这是因为我们指定的模型相当复杂，因为它不仅包括每个单独的变量，还包括它们的所有可能组合（即它们的交互作用），导致一个具有 32 个参数的模型。由于这几乎与数据点（即 48 个儿童的身高）一样多的系数，该模型对数据过拟合，就像我们在 5.4 节中过拟合的初始示例中的复杂多项式曲线一样。

另一种看过拟合效果的方法是看看如果我们随机洗牌权重变量的值会发生什么（在表的第二行显示）。随机洗牌的值应该使得从其他变量预测权重变得不可能，因为它们不应该有系统关系。表中的结果表明，即使没有真正的关系要建模（因为洗牌应该已经消除了关系），复杂模型在拟合数据的预测中仍然显示出非常低的误差，因为它适应了特定数据集中的噪音。然而，当该模型应用于新数据集时，我们看到误差要大得多，正如应该的那样。

14.6.1 交叉验证

为了解决过拟合问题，已经开发出一种称为交叉验证的方法。这种技术通常在机器学习领域中使用，该领域专注于构建能够很好地推广到新数据的模型，即使我们没有新的数据集来测试模型。交叉验证的想法是，我们反复拟合我们的模型，每次都留出一部分数据，然后测试模型预测每个保留子集中的值的能力。

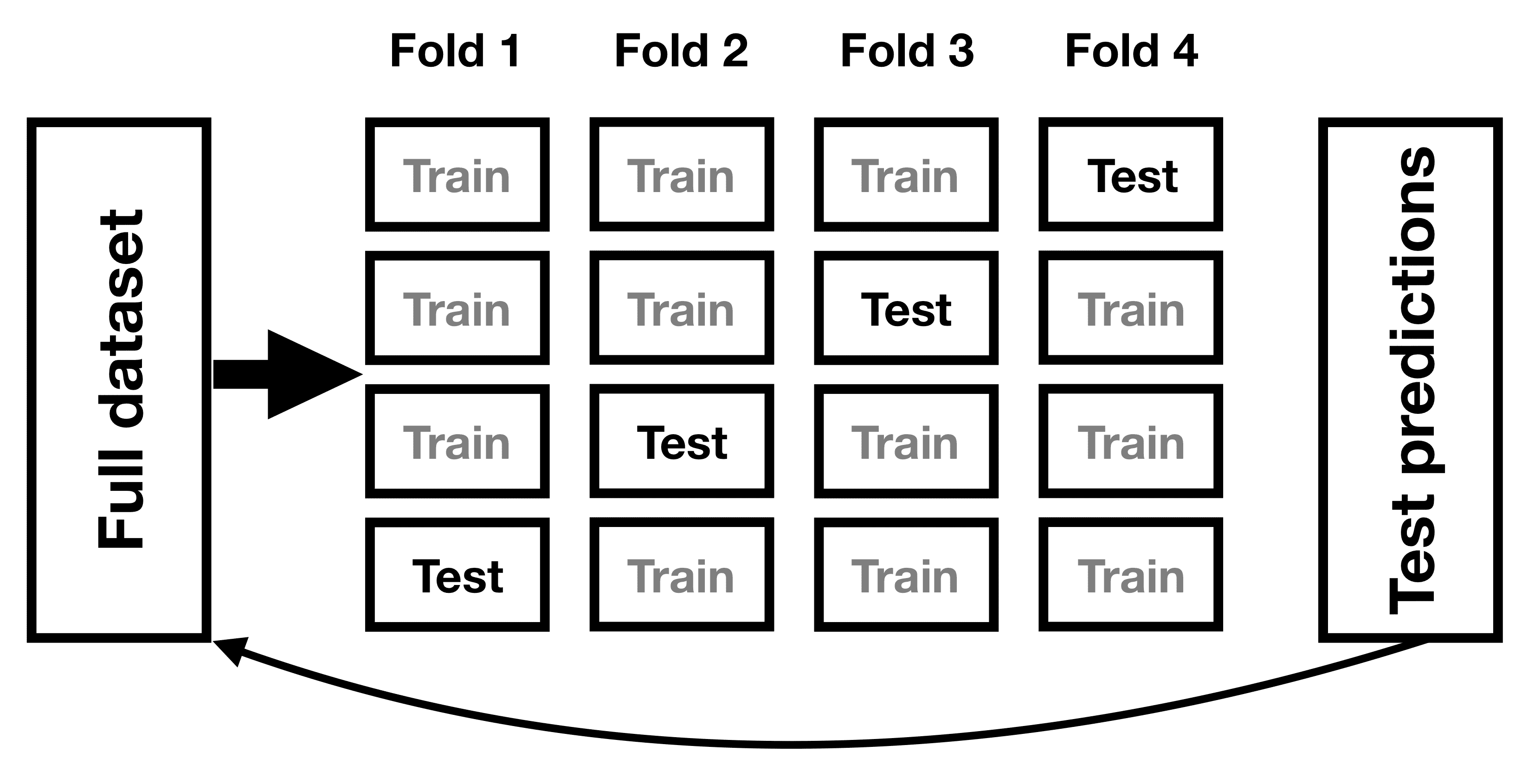
图 14.6：交叉验证程序的示意图。

让我们看看这对我们的体重预测例子会有什么影响。在这种情况下，我们将进行 12 折交叉验证，这意味着我们将数据分成 12 个子集，然后在每种情况下拟合模型 12 次，每次留出一个子集，然后测试模型对这些留出数据点的因变量值的准确预测能力。大多数统计软件都提供工具来对数据应用交叉验证。使用这个函数，我们可以在 NHANES 数据集的 100 个样本上运行交叉验证，并计算交叉验证的 RMSE，以及原始数据和新数据的 RMSE，就像我们上面计算的那样。

表 14.3：交叉验证和新数据的 R 平方，显示交叉验证提供了对模型在新数据上性能的合理估计。

	R 平方
原始数据	0.95
新数据	0.34
交叉验证	0.60

在这里，我们看到交叉验证给出了一个对预测准确性的估计，这个估计比我们在原始数据集上看到的要接近一个全新数据集的情况，实际上，它甚至比一个新数据集的平均值稍微悲观一些，可能是因为只有部分数据被用来训练每个模型。

请注意，正确使用交叉验证是棘手的，建议在实践中使用之前咨询专家。然而，本节希望向你展示了三件事：

• “预测”并不总是意味着你认为的那样

• 复杂模型可能会严重过拟合数据，以至于即使没有真正的信号来预测，也会观察到看似良好的预测

• 除非使用了适当的方法，否则对预测准确性的声明应该持怀疑态度。

14.7 学习目标

阅读完本章后，你应该能够：

• 描述线性回归的概念，并将其应用于数据集

• 描述一般线性模型的概念，并提供其应用示例

• 描述交叉验证如何允许我们估计模型在新数据上的预测性能

14.8 建议阅读

• 统计学习的要素：数据挖掘、推断和预测（第二版） - 机器学习方法的“圣经”，可在网上免费获取。

14.9 附录

14.9.1 估计线性回归参数

我们通常使用线性代数从数据中估计线性模型的参数，线性代数是应用于向量和矩阵的代数形式。如果你不熟悉线性代数，不用担心 - 你实际上不需要在这里使用它，因为 R 会为我们做所有的工作。然而，简短的线性代数探讨可以提供一些关于模型参数在实践中是如何估计的见解。

首先，让我们介绍向量和矩阵的概念；你已经在 R 的上下文中遇到过它们，但我们将在这里进行复习。矩阵是一组按照方形或矩形排列的数字，这样矩阵在一个或多个维度上变化。习惯上，将不同的观测单位（比如人）放在行中，将不同的变量放在列中。让我们拿上面的学习时间数据来说。我们可以将这些数字排列成一个矩阵，它将有八行（每个学生一行）和两列（一个是学习时间，一个是成绩）。如果你在想“这听起来像是 R 中的数据框”，那么你说对了！实际上，数据框是矩阵的一种特殊形式，我们可以使用as.matrix()函数将数据框转换为矩阵。

df <-
 tibble(
 studyTime = c(2, 3, 5, 6, 6, 8, 10, 12) / 3,
 priorClass = c(0, 1, 1, 0, 1, 0, 1, 0)
 ) %>%
 mutate(
 grade = 
 studyTime * betas[1] + 
 priorClass * betas[2] + 
 round(rnorm(8, mean = 70, sd = 5))
 )

df_matrix <- 
 df %>%
 dplyr::select(studyTime, grade) %>%
 as.matrix()

我们可以将一般线性模型用线性代数表示如下：

$$Y=X?\beta +E$$

这看起来很像我们之前使用的方程，只是所有的字母都是大写的，这是为了表达它们是向量的事实。

我们知道成绩数据进入 Y 矩阵，但$X$矩阵中放入了什么？请记住，从我们对线性回归的最初讨论中，我们需要在我们感兴趣的自变量之外添加一个常数，因此我们的$X$矩阵（我们称之为设计矩阵）需要包括两列：一个代表学习时间变量，另一列对于每个个体都具有相同的值（通常我们用全为 1 的值填充）。我们可以以图形方式查看生成的设计矩阵（参见图 14.7）。

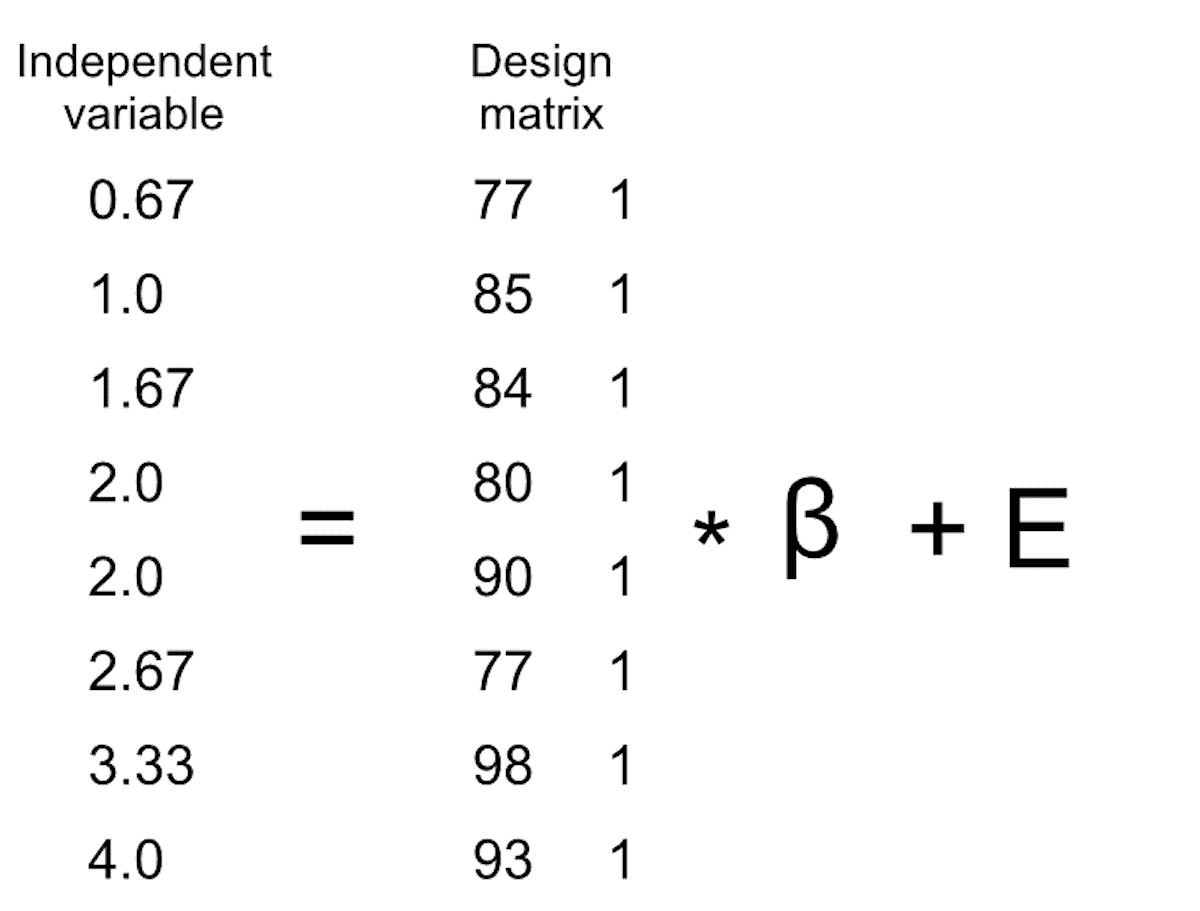
图 14.7：用矩阵代数表示学习时间数据的线性模型的描绘。

矩阵乘法规则告诉我们，矩阵的维度必须相互匹配；在这种情况下，设计矩阵的维度为 8（行）X 2（列），Y 变量的维度为 8 X 1。因此，$\beta$矩阵的维度需要为 2 X 1，因为 8 X 2 矩阵乘以 2 X 1 矩阵的结果是 8 X 1 矩阵（因为匹配的中间维度被消除）。$\beta$矩阵中的两个值的解释是它们分别与学习时间和 1 相乘，以获得每个个体的估计成绩。我们还可以将线性模型视为每个个体的一组单独方程：

${\hat{y}}_1=studyTim{e}_1?{\beta }_1+1?{\beta }_2$

${\hat{y}}_2=studyTim{e}_2?{\beta }_1+1?{\beta }_2$

…

${\hat{y}}_8=studyTim{e}_8?{\beta }_1+1?{\beta }_2$

请记住，我们的目标是确定给定$X$和$Y$的已知值的最佳拟合值$\beta$。一个天真的方法是使用简单的代数来解决$\beta$ – 在这里我们忽略了误差项$E$，因为它不在我们的控制范围内：

$$\hat{\beta }=\frac{Y}{X}$$

这里的挑战是$X$和$\beta$现在是矩阵，而不是单个数字 – 但线性代数的规则告诉我们如何除以矩阵，这与乘以矩阵的逆（称为$X^{?1}$）相同。我们可以在 R 中这样做：

# compute beta estimates using linear algebra

#create Y variable 8 x 1 matrix
Y <- as.matrix(df$grade) 
 #create X variable 8 x 2 matrix
X <- matrix(0, nrow = 8, ncol = 2)
#assign studyTime values to first column in X matrix
X[, 1] <- as.matrix(df$studyTime) 
#assign constant of 1 to second column in X matrix
X[, 2] <- 1 

# compute inverse of X using ginv()
# %*% is the R matrix multiplication operator

beta_hat <- ginv(X) %*% Y #multiple the inverse of X by Y
print(beta_hat)

##      [,1]
## [1,]  8.2
## [2,] 68.0

对于对统计方法感兴趣的任何人，强烈建议投入一些时间学习线性代数，因为它为标准统计中使用的几乎所有工具提供了基础。

参考资料

Copas, J. B. 1983. “Regression, Prediction and Shrinkage (with Discussion).” Journal of the Royal Statistical Society, Series B: Methodological 45: 311–54.