蓝桥杯专题-真题版含答案-【国庆星期日】【三色棋】【蒙地卡罗法求 PI】【格雷码(Gray Code)】
| Unity3D特效百例 | 案例项目实战源码 | Android-Unity实战问题汇总 |
|---|---|---|
| 游戏脚本-辅助自动化 | Android控件全解手册 | 再战Android系列 |
| Scratch编程案例 | 软考全系列 | Unity3D学习专栏 |
| 蓝桥系列 | ChatGPT和AIGC |
👉关于作者
专注于Android/Unity和各种游戏开发技巧,以及各种资源分享(网站、工具、素材、源码、游戏等)
有什么需要欢迎底部卡片私我,获取更多支持,交流让学习不再孤单。

👉实践过程
😜国庆星期日
/* 国庆星期日
1949年的国庆节(10月1日)是星期六。
今年(2012)的国庆节是星期一。
那么,从建国到现在,有几次国庆节正好是星期日呢?
只要答案,不限手段!
可以用windows日历,windows计算器,Excel公式,。。。。。
当然,也可以编程!
不要求写出具体是哪些年,只要一个数目!
public class T17 {
public static int calc(int n,int m,int d){
int[][] days = {{0,31,28,31,30,31,30,31,31,30,31,30,31}, // 平年
{0,31,29,31,30,31,30,31,31,30,31,30,31}};// 闰年
int b = 0; // 默认为平年
if(n%4==0&&n%100!=0||n%400==0) b = 1; // 是闰年
int sum = d;
for(int i=0;i<m;i++){
sum += days[b][i];
}
return sum;
}
public static void main(String[] args){
int count = 0;
// 1949年的国庆节(10月2日)是星期日。
// 得到这年10月2号后的的剩余天数
int total = calc(1949,12,31)-calc(1949,10,2);
for(int i=1950;i<2012;i++){
// calc(i)计算每年的10月1日是这一年的第天数,再用总天数对7取余==0说明是周日
total += calc(i,10,1); // 计算当年到10月1的总天数
if(total%7==0){
System.out.println(i+"年10月1日");
count++; // 次数加1
}
}
System.out.println("总数:"+count);
}
}
😜三色棋
说明
三色旗的问题最早由E.W.Dijkstra所提出,他所使用的用语为Dutch Nation Flag(Dijkstra为荷兰人),而多数的作者则使用Three-Color Flag来称之。
假设有一条绳子,上面有红、白、蓝三种颜色的旗子,起初绳子上的旗子颜色并没有顺序,您希望将之分类,并排列为蓝、白、红的顺序,要如何移动次数才会最少,注意您只能在绳子上进行这个动作,而且一次只能调换两个旗子。
解法
在一条绳子上移动,在程式中也就意味只能使用一个阵列,而不使用其它的阵列来作辅助,问题的解法很简单,您可以自己想像一下在移动旗子,从绳子开头进行,遇到蓝色往前移,遇到白色留在中间,遇到红色往后移,如下所示:
只是要让移动次数最少的话,就要有些技巧:
如果图中W所在的位置为白色,则W+1,表示未处理的部份移至至白色群组。
如果W部份为蓝色,则B与W的元素对调,而B与W必须各+1,表示两个群组都多了一个元素。
如果W所在的位置是红色,则将W与R交换,但R要减1,表示未处理的部份减1。
注意B、W、R并不是三色旗的个数,它们只是一个移动的指标;什幺时候移动结束呢?一开始时未处理的R指标会是等于旗子的总数,当R的索引数减至少于W的索引数时,表示接下来的旗子就都是红色了,此时就可以结束移动,如下所示:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define BLUE 'b'
#define WHITE 'w'
#define RED 'r'
#define SWAP(x, y) { char temp; \
temp = color[x]; \
color[x] = color[y]; \
color[y] = temp; }
int main() {
char color[] = {'r', 'w', 'b', 'w', 'w',
'b', 'r', 'b', 'w', 'r', '\0'};
int wFlag = 0;
int bFlag = 0;
int rFlag = strlen(color) - 1;
int i;
for(i = 0; i < strlen(color); i++)
printf("%c ", color[i]);
printf("\n");
while(wFlag <= rFlag) {
if(color[wFlag] == WHITE)
wFlag++;
else if(color[wFlag] == BLUE) {
SWAP(bFlag, wFlag);
bFlag++; wFlag++;
}
else {
while(wFlag < rFlag && color[rFlag] == RED)
rFlag--;
SWAP(rFlag, wFlag);
rFlag--;
}
}
for(i = 0; i < strlen(color); i++)
printf("%c ", color[i]);
printf("\n");
return 0;
}
😜蒙地卡罗法求 PI
说明蒙地卡罗为摩洛哥王国之首都,该国位于法国与义大利国境,以赌博闻名。蒙地卡罗的基本原理为以乱数配合面积公式来进行解题,这种以机率来解题的方式带有赌博的意味,虽然在精确度上有所疑虑,但其解题的思考方向却是个值得学习的方式。
解法蒙地卡罗的解法适用于与面积有关的题目,例如求PI值或椭圆面积,这边介绍如何求PI值;假设有一个圆半径为1,所以四分之一圆面积就为PI,而包括此四分之一圆的正方形面积就为1,如下图所示:
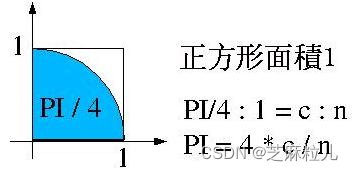
如果随意的在正方形中投射飞标(点)好了,则这些飞标(点)有些会落于四分之一圆内,假设所投射的飞标(点)有n点,在圆内的飞标(点)有c点,则依比例来算,就会得到上图中最后的公式。
至于如何判断所产生的点落于圆内,很简单,令乱数产生X与Y两个数值,如果X2+Y2等于1就是落在圆内。
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define N 50000
int main(void) {
int i, sum = 0;
double x, y;
srand(time(NULL));
for(i = 1; i < N; i++) {
x = (double) rand() / RAND_MAX;
y = (double) rand() / RAND_MAX;
if((x * x + y * y) < 1)
sum++;
}
printf("PI = %f\n", (double) 4 * sum / N);
return 0;
}
😜格雷码(Gray Code)
说明
Gray Code是一个数列集合,每个数使用二进位来表示,假设使用n位元来表示每个数好了,任两个数之间只有一个位元值不同,例如以下为3位元的Gray Code:
000 001 011 010 110 111 101 100
由定义可以知道,Gray Code的顺序并不是唯一的,例如将上面的数列反过来写,也是一组Gray Code:
100 101 111 110 010 011 001 000
Gray Code是由贝尔实验室的Frank Gray在1940年代提出的,用来在使用PCM(Pusle Code Modulation)方法传送讯号时避免出错,并于1953年三月十七日取得美国专利。
解法
由于Gray Code相邻两数之间只改变一个位元,所以可观 察Gray Code从1变0或从0变1时的位置,假设有4位元的Gray Code如下:
0000 0001 0011 0010 0110 0111 0101 0100
1100 1101 1111 1110 1010 1011 1001 1000
观察奇数项的变化时,我们发现无论它是第几个Gray Code,永远只改变最右边的位元,如果是1就改为0,如果是0就改为1。
观察偶数项的变化时,我们发现所改变的位元,是由右边算来第一个1的左边位元。
以上两个变化规则是固定的,无论位元数为何;所以只要判断位元的位置是奇数还是偶数,就可以决定要改变哪一个位元的值,为了程式撰写方便,将阵列索引 0当作最右边的值,而在列印结果时,是由索引数字大的开始反向列印。
将2位元的Gray Code当作平面座标来看,可以构成一个四边形,您可以发现从任一顶点出发,绕四边形周长绕一圈,所经过的顶点座标就是一组Gray Code,所以您可以得到四组Gray Code。
同样的将3位元的Gray Code当作平面座标来看的话,可以构成一个正立方体,如果您可以从任一顶点出发,将所有的边长走过,并不重复经过顶点的话,所经过的顶点座标顺序之组合也就是一组Gray Code。
#include <stdio.h>
#include <stdlib.h>
#define MAXBIT 20
#define TRUE 1
#define CHANGE_BIT(x) x = ((x) == '0' ? '1' : '0')
#define NEXT(x) x = (1 - (x))
int main(void) {
char digit[MAXBIT];
int i, bits, odd;
printf("输入位元数:");
scanf("%d", &bits);
for(i = 0; i < bits; i++) {
digit[i] = '0';
printf("0");
}
printf("\n");
odd = TRUE;
while(1) {
if(odd)
CHANGE_BIT(digit[0]);
else {
// 计算第一个1的位置
for(i = 0; i < bits && digit[i] == '0'; i++) ;
if(i == bits - 1) // 最后一个Gray Code
break;
CHANGE_BIT(digit[i+1]);
}
for(i = bits - 1; i >= 0; i--)
printf("%c", digit[i]);
printf("\n");
NEXT(odd);
}
return 0;
}
👉其他
📢作者:小空和小芝中的小空
📢转载说明-务必注明来源:https://zhima.blog.csdn.net/
📢这位道友请留步??,我观你气度不凡,谈吐间隐隐有王者霸气💚,日后定有一番大作为📝!!!旁边有点赞👍收藏🌟今日传你,点了吧,未来你成功??,我分文不取,若不成功??,也好回来找我。
温馨提示:点击下方卡片获取更多意想不到的资源。

本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 4.STM32F40x 串口通信(文中以USART1为例子)
- 【Python基础入门篇】基本函数——os与sys模块
- weblogic 内存溢出调优方法
- 算法基础之染色法判定二分图
- 鸿蒙项目方舟框架(ArkUI)之线性布局容器Stack组件
- mybatis中的xml语法
- Python 类
- 2024年美赛数学建模思路 - 案例:感知机原理剖析及实现
- 9.【TypeScript 教程】接口(Interface)
- Python调试技巧和性能优化策略技巧全解析