二叉树基础oj练习(对称二叉树、翻转二叉树、另一棵树的子树二叉树的构建及遍历)
发布时间:2024年01月08日
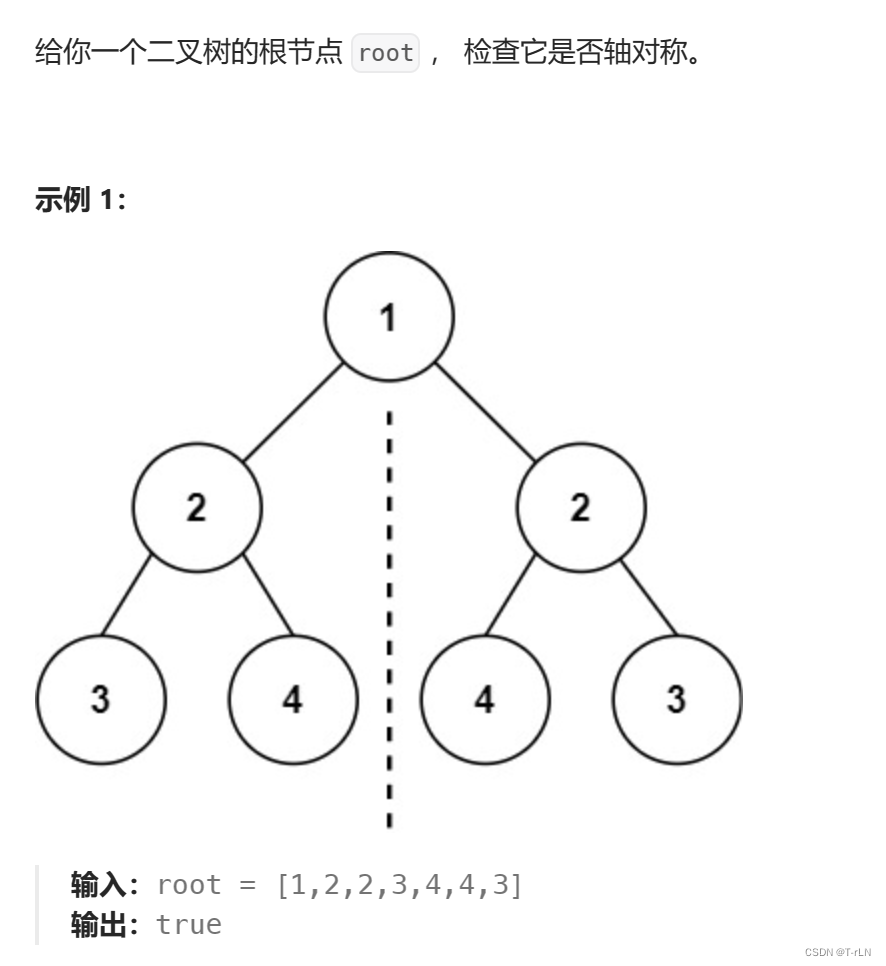
1.对称二叉树
题目详情
代码
bool _isSymmetric(struct TreeNode* root1,struct TreeNode* root2)
{
if(root1==NULL&&root2==NULL)//都为空
return true;
if(root1==NULL||root2==NULL)//一个是空一个不是
return false;
if(root1->val!=root2->val)
return false; //根部分已经判断完成
return _isSymmetric(root1->left,root2->right)
&&_isSymmetric(root1->right,root2->left);
}
bool isSymmetric(struct TreeNode* root) {
return _isSymmetric(root->left,root->right);
}
思路
我们以“相同的树”那题思路拓展开,先创建子函数,传入左节点和右节点(要看是否对称,比较两边)
大的思路:先看根存在或相同否,根判断完后。开始左子树,递归调用函数。接着右子树也同理
聚焦于递归:函数的主体只是比较那个“根”的情况,但是每个子节点也是根,递归调用后,他们在他们的函数里就是根(所以来判断他们的相等或者为空情况),最后都是遇到空(到了整体树的叶),就停止了
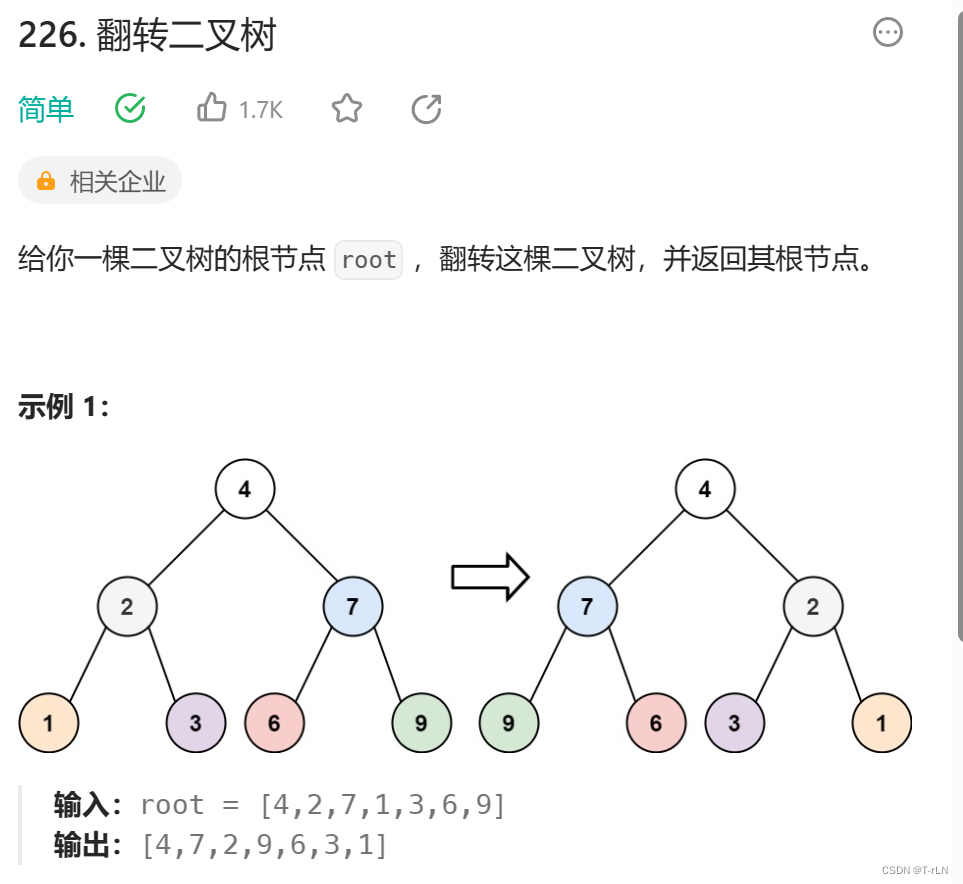
2.翻转二叉树
题目详情
代码
struct TreeNode* invertTree(struct TreeNode* root) {
if(root==NULL)
return NULL;
struct TreeNode* root1=invertTree(root->left);
struct TreeNode* root2=invertTree(root->right);
root->left=root2;//真翻转
root->right=root1;//真翻转
return root;
}
思路
很明确的一点是:我们要从根节点开始,递归地对树进行遍历
具体的实现方法:叶子节点先开始翻转(叶子下面都是NULL,交换后也没意义,叶子也是利用那两条“真翻转”语句来进行交换,交换后返回,去进行上一级节点)。
宏观上:如果当前遍历到的节点root的左右两棵子树都已经翻转,那么我们只需要交换两棵子树的位置,就完成了
通过递归的方式翻转左子树和右子树,并将左子树指向翻转后的右子树,右子树指向翻转后的左子树,最后返回当前节点
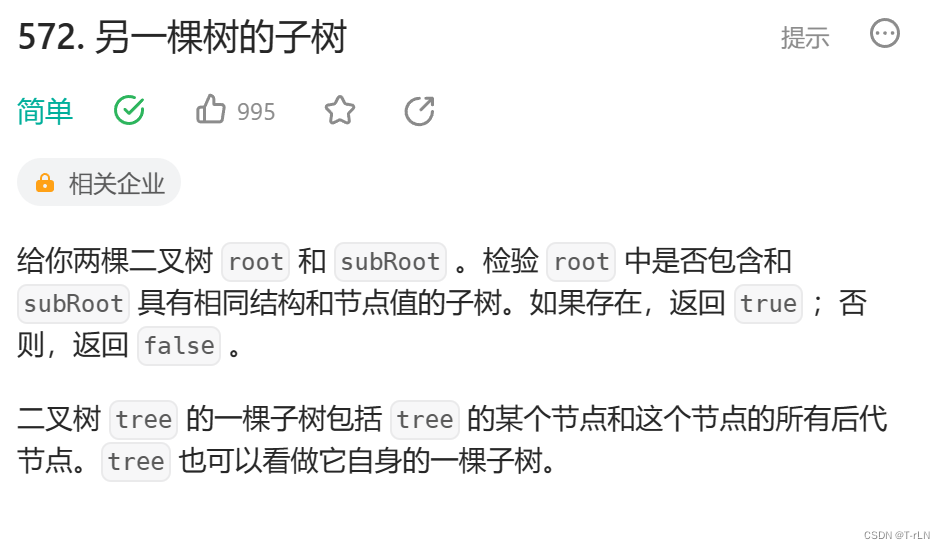
3.另一颗树的子树
题目详情

代码1
bool isSameTree(struct TreeNode* q,struct TreeNode* p)
{
if(q==NULL&&p==NULL)
{
return true;
}
if(q==NULL||p==NULL)
{
return false;
}
if(q->val!=p->val)
{
return false;
}
return isSameTree(q->left,p->left)
&&isSameTree(q->right,p->right);
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){
if(root==NULL)
{
return false;
}
if(root->val==subRoot->val)
{
if(isSameTree(root,subRoot))
{
return true;
}
}
return isSubtree(root->left,subRoot)||isSubtree(root->right,subRoot);
}
思路1
我们借用一下isSameTree的代码(来判断两个树是不是相同的),这题也是看
root的子树有没有跟subroot有没有相同的。还是先处理根(因为每个左右子树进去后也是根)
要是val一相同,再看是不是一个树,要是就返回true了,不是就看左子树和右子树是不是
代码2
bool isSameTree(struct TreeNode* q,struct TreeNode* p)
{
if(q==NULL&&p==NULL)
{
return true;
}
if(q==NULL||p==NULL)
{
return false;
}
if(q->val!=p->val)
{
return false;
}
return isSameTree(q->left,p->left)
&&isSameTree(q->right,p->right);
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){
if(root==NULL)
{
return false;
}
return isSameTree(root,subRoot)||
isSubtree(root->left,subRoot)||isSubtree(root->right,subRoot);
}
思路2
现在成了“三选一”了,也很好理解:三种情况有一种为真就返回true了
背后还是同一种思路不同的写法,背后的逻辑关系是一样的:看似少了一句root->val==subRoot->val,但是本身isSameTree就能进行跟是否相同的判断
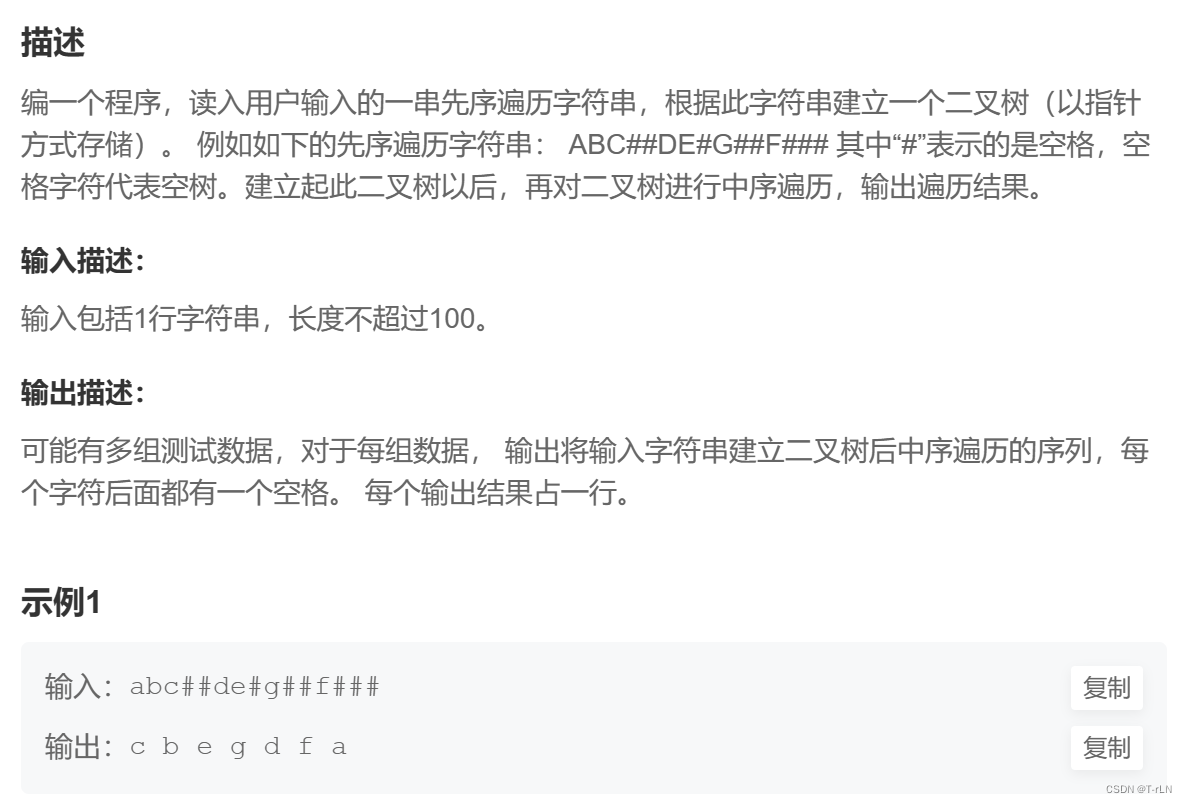
4.二叉树的构建及遍历
题目详情
代码
#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include<assert.h>
#include<stdlib.h>
typedef char BTDataType;
typedef struct BinaryTreeNode { //节点
BTDataType data;//数据
struct BinaryTreeNode* left;//左孩子
struct BinaryTreeNode* right;//右孩子
} TreeNode;
TreeNode* createTree(char* arr, int* pi) {
if (arr[*pi] == '#' || arr[*pi] == '\0') {
(*pi)++;
return NULL;
}
TreeNode* root = (TreeNode*)malloc(sizeof(TreeNode));
assert(root);
root->data = arr[*pi];
(*pi)++;
root->left = createTree(arr, pi);
root->right = createTree(arr, pi);
return root;
}
void PreOrder(TreeNode* root) {
if (root == NULL) {
return;
}
PreOrder(root->left);
printf("%c ", root->data);
PreOrder(root->right);
}
int main() {
char arr[100] = { 0 };
scanf("%s", arr);
int i = 0;
TreeNode* root = createTree(arr, &i);
PreOrder(root);
return 0;
}
今天就到这里啦!
文章来源:https://blog.csdn.net/qq_74415153/article/details/135175147
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- drf知识-06
- 【Linux工具篇】编辑器vim
- 前端密钥怎么存储,以及临时存储一些数据,如何存储才最安全?
- ubuntu安装kibana
- Linux引导和服务管理
- 173.【2023年华为OD机试真题(C卷)】用连续自然数之和来表达整数(双指针法实现Java&Python&C++&&JS)
- Adobe Premier及PrElements各版本安装指南
- QT+OSG/osgEarth编译之五十八:3ds+Qt编译(一套代码、一套框架,跨平台编译,版本:OSG-3.6.5插件库osgdb_3ds)
- 为突发事件提供高现势性数据支撑!大势智慧助力中山市2023应急测绘保障演练举行
- GPU的硬件架构