《机器学习》客户流失判断-python实现

题目

赛题描述

给定企业客户信息，建立分类模型，判断企业客户是否会流失。

数据说明

数据主要包括企业客户样本信息。 数据分为训练数据和测试数据，分别保存在train.csv和test_noLabel.csv两个文件中。 字段说明如下：
（1）ID：编号
（2）Contract：是否有合同
（3）Dependents：是否有家属
（4）DeviceProtection：是否有设备保护
（5）InternetService：是否有互联网服务
（6）MonthlyCharges：月度费用
（7）MultipleLines：是否有多条线路
（8）Partner：是否有配偶
（9）PaymentMethod：付款方式
（10）PhoneService：是否有电话服务
（11）SeniorCitizen：是否为老年人
（12）TVProgram：是否有电视节目
（15）TotalCharges：总费用
（16）gender：用户性别
（17）tenure：任期年数
（18）Churn：用户是否流失
如遇数据下载打开乱码问题： 不要用excel打开,用notepad++或者vs code。文件格式是通用的编码方式utf-8。

赛题来源-DataCastle

https://challenge.datacastle.cn/v3/cmptDetail.html?id=356

数据可在网站上下载

问题描述

通过题目给定的企业客户信息，选择适当的分类算法，建立多个分类模型，使用准确率指标评估模型性能，准确率越高，说明正确预测出企业客户流失情况的效果越好，以此找到最优的分类模型用于预测企业客户是否会流失。通过模型可以帮助企业更好地了解客户流失的趋势，从而采取相应的措施来维护客户关系。

解题思路

数据预处理：

1.检查处理缺失值、重复值、异常值
2.标签编码转化

数据可视化：
3. 各标签对流失率的影响
4. 相关性热力图绘制

建立分类模型与对比模型：
朴素贝叶斯、AdaBoost、逻辑回归、KNN、SVM、
随机森林、XGBoost、MLP、 LightGBM、GBDT、
随机森林-MLP-XGBoost组合模型

使用随机搜索及贝叶斯优化 进行超参数调优

Python实现

读取数据并初步了解

导入宏包

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import stats
from scipy.special import boxcox1p
import missingno as msno
import warnings
warnings.filterwarnings("ignore")
%matplotlib inline

读取数据

train = pd.read_csv('train.csv')
test = pd.read_csv('test_noLabel.csv')
train.shape,test.shape

train.head()
test.head()

查看数据类型

train.info()
test.info()

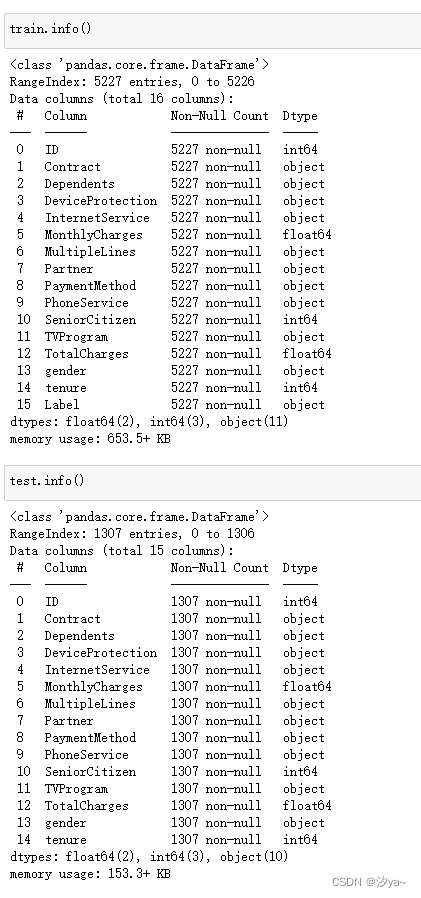
检查缺失值

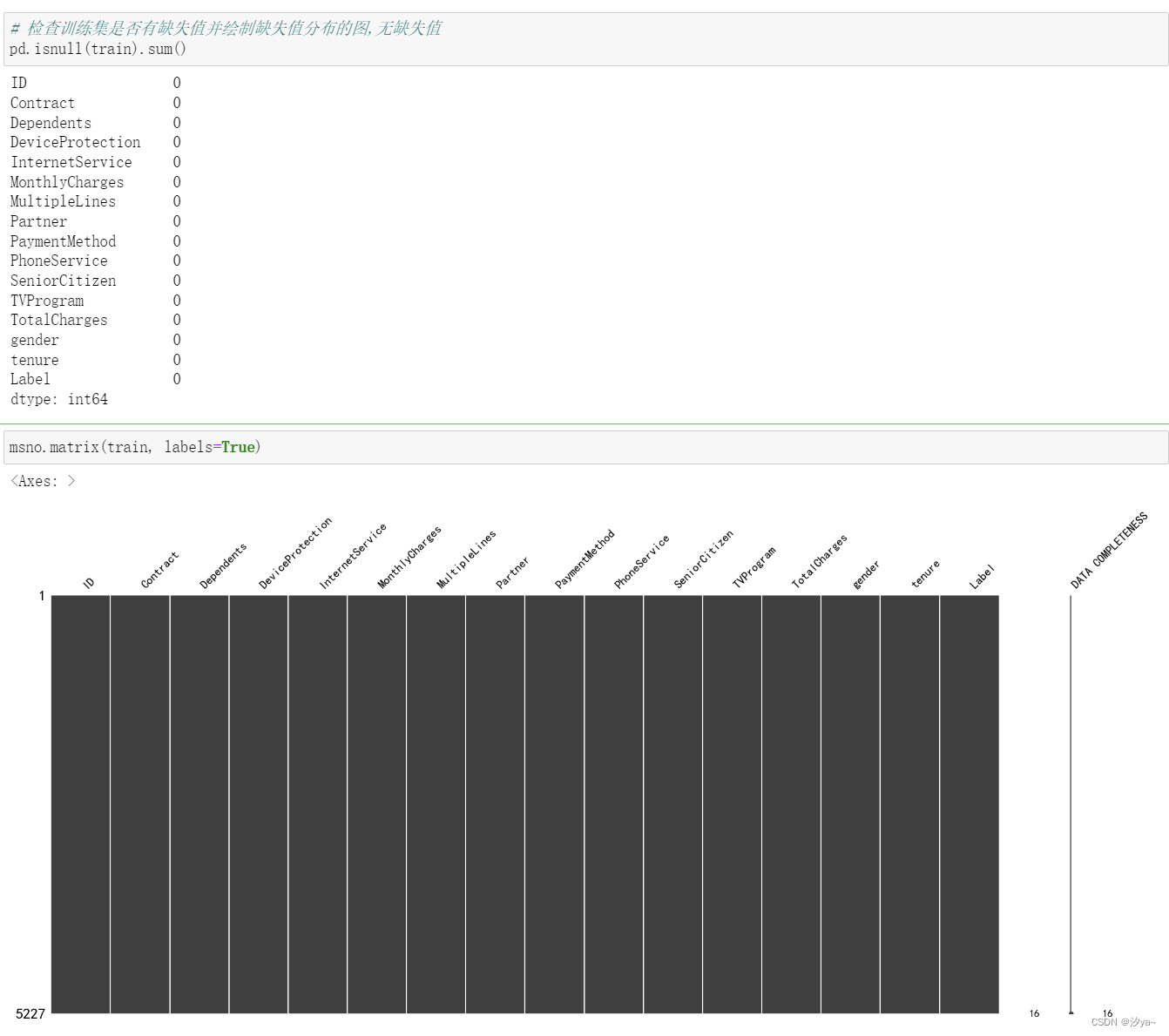
使用 pd.isnull(train).sum() 查看缺失值情况。并通过 msno.matrix() 绘制缺失值热力图，从结果可以看出数据集不存在缺失值

# 检查训练集是否有缺失值并绘制缺失值分布的图,无缺失值
pd.isnull(train).sum()

msno.matrix(train, labels=True)

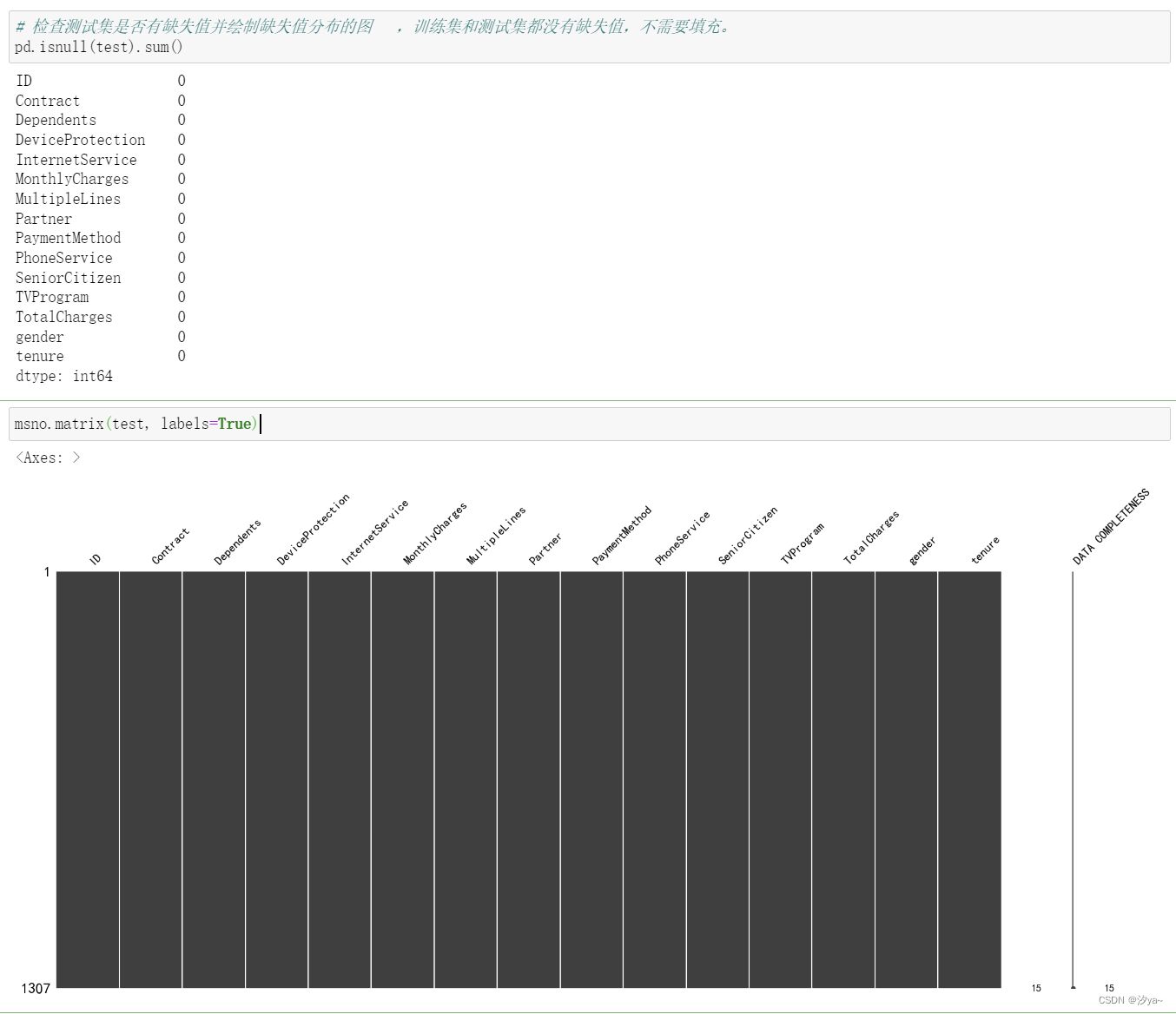
# 检查测试集是否有缺失值并绘制缺失值分布的图   ，训练集和测试集都没有缺失值，不需要填充。
pd.isnull(test).sum()
msno.matrix(test, labels=True)

描述性统计分析

使用 train.describe().T 对数值型列进行描述性统计分析，包括平均值、标准差、最大值、最小值等。

train.describe()
test.describe()

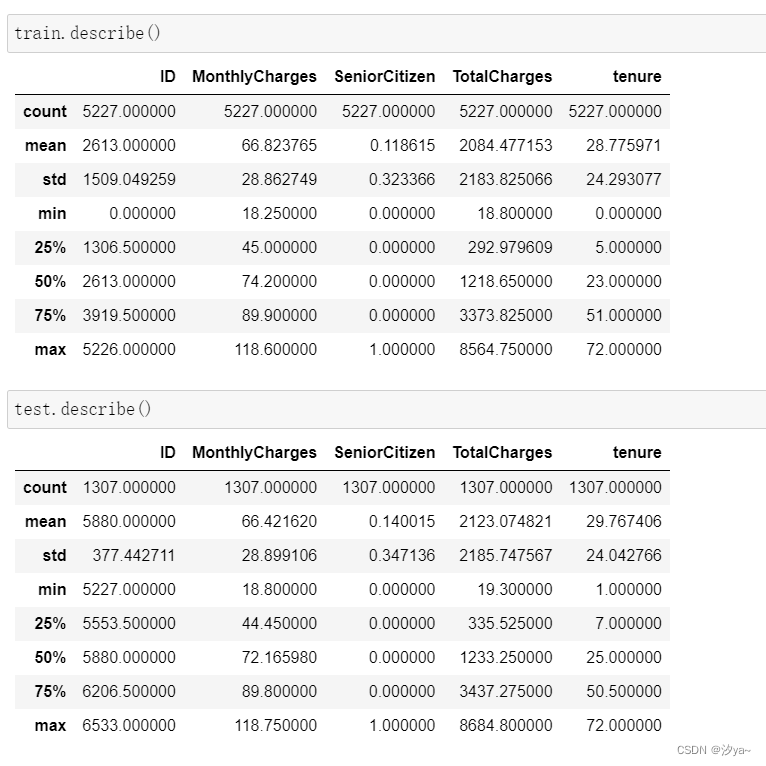
这份数据描述统计结果提供了关于客户信息的多个方面的信息。其中包括每月费用的平均值约为66.82，老年人占比约为11.86%，客户的平均任期约为 28.78个月，以及总费用的平均值约为2084.48。这些数据能够描绘出客户的消费情况、老年人比例以及服务使用时长等信息，另外提供查看最大最小 值，可以初步确定数据无逻辑异常。

可视化分析

用户流失分析

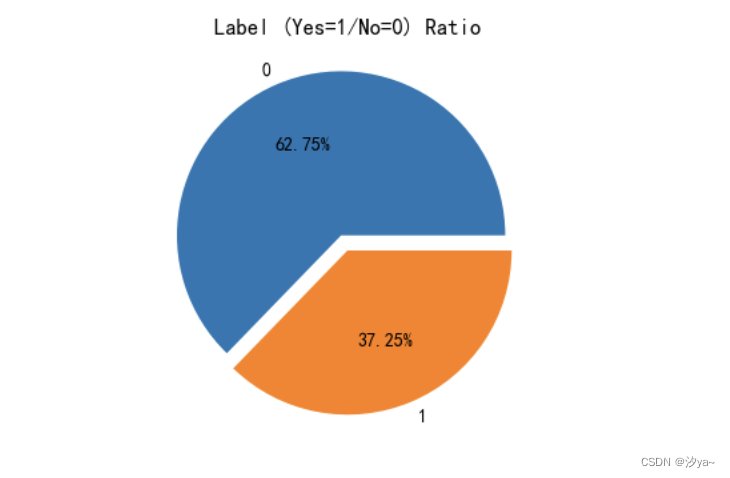
使用 train['Label'].value_counts() 统计不同标签（流失与否）的数量。并绘制了用户流失比例的扇形图和不同特征对客户流失率的影响的柱状 图。通过结果可以看出数据集中有62.75%用户没流失，337.25%客户流失，数据集是不均衡。

#流失用户数量和占比
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = 4, 4
plt.pie(train['Label'].value_counts(), labels=train['Label'].value_counts().index, autopct='%1.2f%%', explode=(0.1, 0))
plt.title('Label (Yes=1/No=0) Ratio')
plt.show()

特征分析

#用户属性柱状图
import seaborn as sns
import matplotlib.pyplot as plt

# 设置中文字体为 SimHei
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题

# 设置图表尺寸
plt.rcParams['figure.figsize'] = (12, 10)

# 绘制性别对客户流失率的影响
plt.subplot(2, 2, 1)
sns.countplot(x='gender', hue='Label', data=train)
plt.title('性别对客户流失率的影响')

# 绘制老人对客户流失率的影响
plt.subplot(2, 2, 2)
sns.countplot(x='SeniorCitizen', hue='Label', data=train)
plt.title('老人对客户流失率的影响')

# 绘制配偶对客户流失率的影响
plt.subplot(2, 2, 3)
sns.countplot(x='Partner', hue='Label', data=train)
plt.title('配偶对客户流失率的影响')

# 绘制亲属对客户流失率的影响
plt.subplot(2, 2, 4)
sns.countplot(x='Dependents', hue='Label', data=train)
plt.title('亲属对客户流失率的影响')

# 显示图表
plt.show()

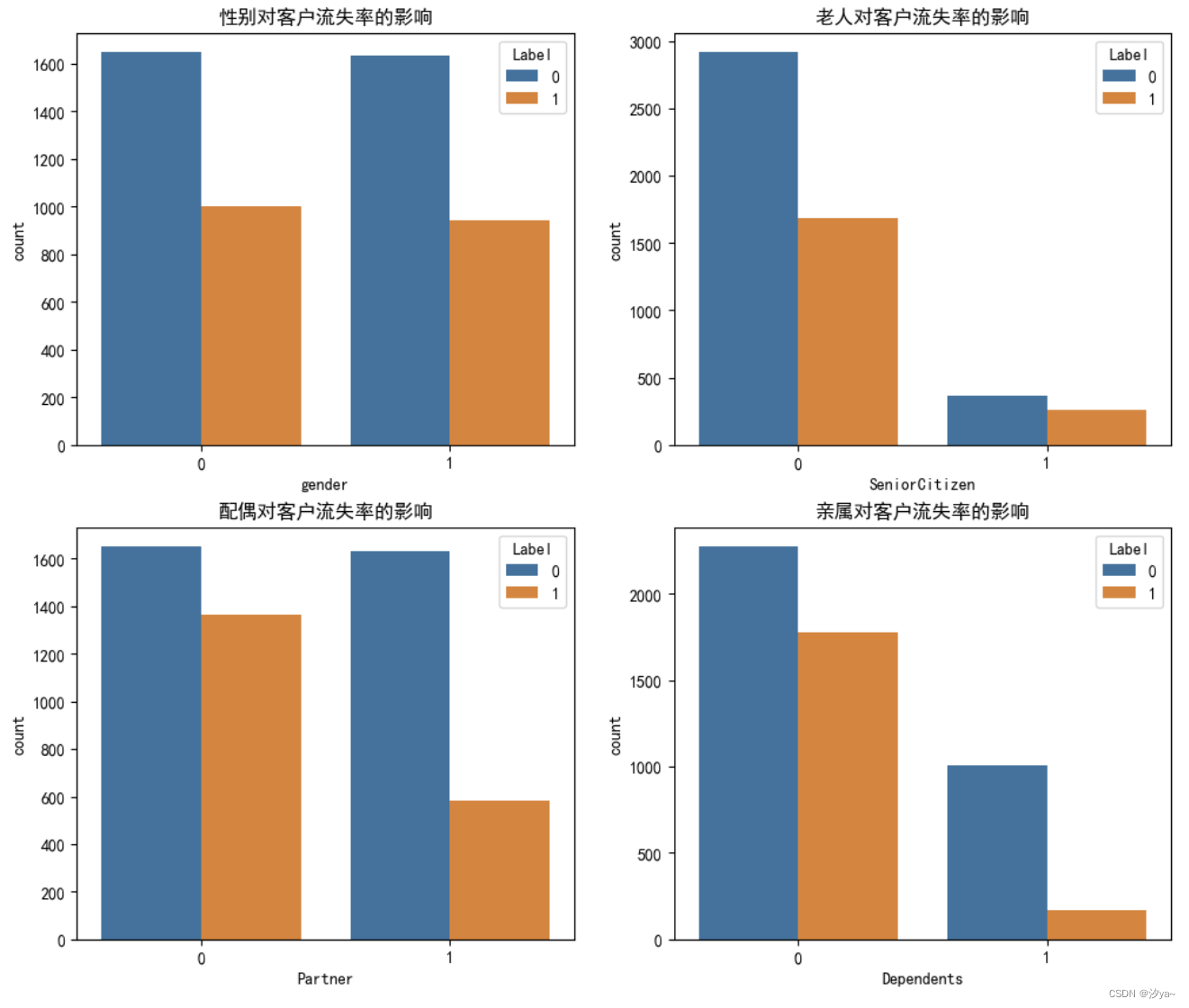
对于性别、老人、配偶、亲属等特征，使用 sns.countplot() 绘制柱状图，分析其对客户流失率的影响。
可以得出下面结论：
1. 性别对用户流失影响不大；
2. 年轻用户的流失率显著高于年长用户；
3. 有伴侣的用户流失比例低于无伴侣用户；
4. 用户中有家属的数量较少；
5. 有家属的用户流失比例低于无家属用户。

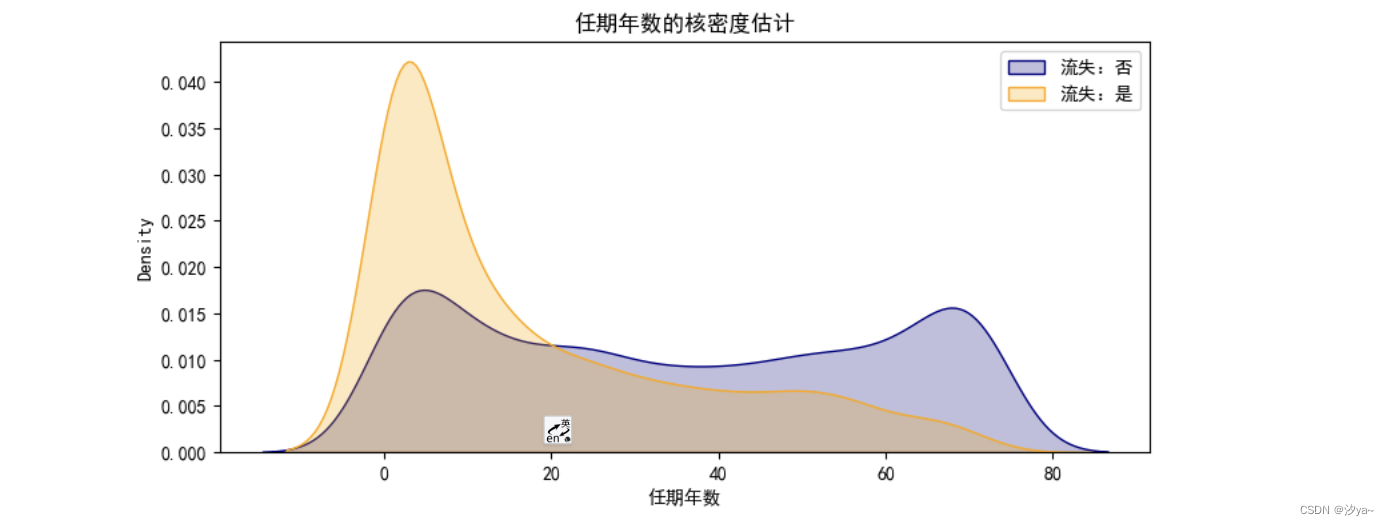
任期年数与客户流失的关系：

使用 sns.kdeplot() 绘制核密度估计图，在网时长越久，流失率越低，符合一般经验；在网时间达到三个月，流失率小于在网率，证明用户心理稳定 期一般是三个月。

import seaborn as sns
import matplotlib.pyplot as plt

# 设置中文字体为 SimHei
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题

# Kernel density estimaton核密度估计
def kdeplot(feature, xlabel, df):
    plt.figure(figsize=(9, 4))
    plt.title("{0}的核密度估计".format(xlabel))  # 中文标题
    ax0 = sns.kdeplot(df[df['Label'] == 'No'][feature].dropna(), color='navy', label='流失：否', shade='True')
    ax1 = sns.kdeplot(df[df['Label'] == 'Yes'][feature].dropna(), color='orange', label='流失：是', shade='True')
    plt.xlabel(xlabel)
    plt.legend(fontsize=10)

# 调用函数绘制核密度图
kdeplot('tenure', '任期年数',train )
plt.show()

# 在网时长越久，流失率越低，符合一般经验；
# 在网时间达到三个月，流失率小于在网率，证明用户心理稳定期一般是三个月。

# 这个核密度估计图展示了用户任期年数 (`tenure`) 与客户流失 (`Label`) 的关系。在这张图中：

# - **横轴 (`tenure`):** 表示用户的任期年数。这个轴展示了用户在服务提供商（可能是电信公司等）停留的时间跨度。
  
# - **纵轴（密度）:** 表示在每个任期年数上流失与不流失客户的密度估计。密度估计通常显示了不同任期年数上客户流失的相对频率。在这里，越高的密度意味着在特定的任期年数上，流失或不流失的用户数量较多。

# - **曲线:** 图中有两条曲线，一条代表流失为 "No"（蓝色），另一条代表流失为 "Yes"（橙色）。这两条曲线代表了任期年数对于流失与否的概率密度分布。当曲线较高的区域重叠时，表示在这些任期年数上流失与不流失的用户数量相近；而当曲线差异较大时，则代表在该任期年数上流失和不流失的用户数量有显著差异。

# 这个图可以帮助你理解在不同的任期年数下，用户流失和不流失的趋势。例如，你可以观察到在哪些任期年数上流失率较高或较低，以及是否存在明显的任期年数区间，对流失率有重要影响。

服务类属性分析

#服务属性分析
import seaborn as sns
import matplotlib.pyplot as plt
# 设置中文字体为 SimHei
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题

# 设置图表尺寸
plt.figure(figsize=(10, 5))

# 绘制 MultipleLines 对用户流失的影响的柱状图
plt.subplot(1, 2, 1)  # 创建第一个子图
sns.countplot(x='MultipleLines', hue='Label', data=train)
plt.title('多条线路对用户流失的影响')
plt.xlabel('是否有多条线路')
plt.ylabel('用户数量')
plt.legend(title='流失')

# 绘制 InternetService 对用户流失的影响的柱状图
plt.subplot(1, 2, 2)  # 创建第二个子图
sns.countplot(x='InternetService', hue='Label', data=train)
plt.title('互联网服务对用户流失的影响')
plt.xlabel('是否有互联网服务')
plt.ylabel('用户数量')
plt.legend(title='流失')

# 调整子图布局
plt.tight_layout()

# 显示图表
plt.show()

使用 sns.countplot() 分析不同服务属性对用户流失的影响，如多条线路和互联网服务。
电话服务整体对用户流失影响较大。
单光纤用户的流失占比较高；
光纤用户绑定了安全、备份、保护、技术支持服务的流失率较低；
光纤用户附加流媒体电视、电影服务的流失率占比较低。

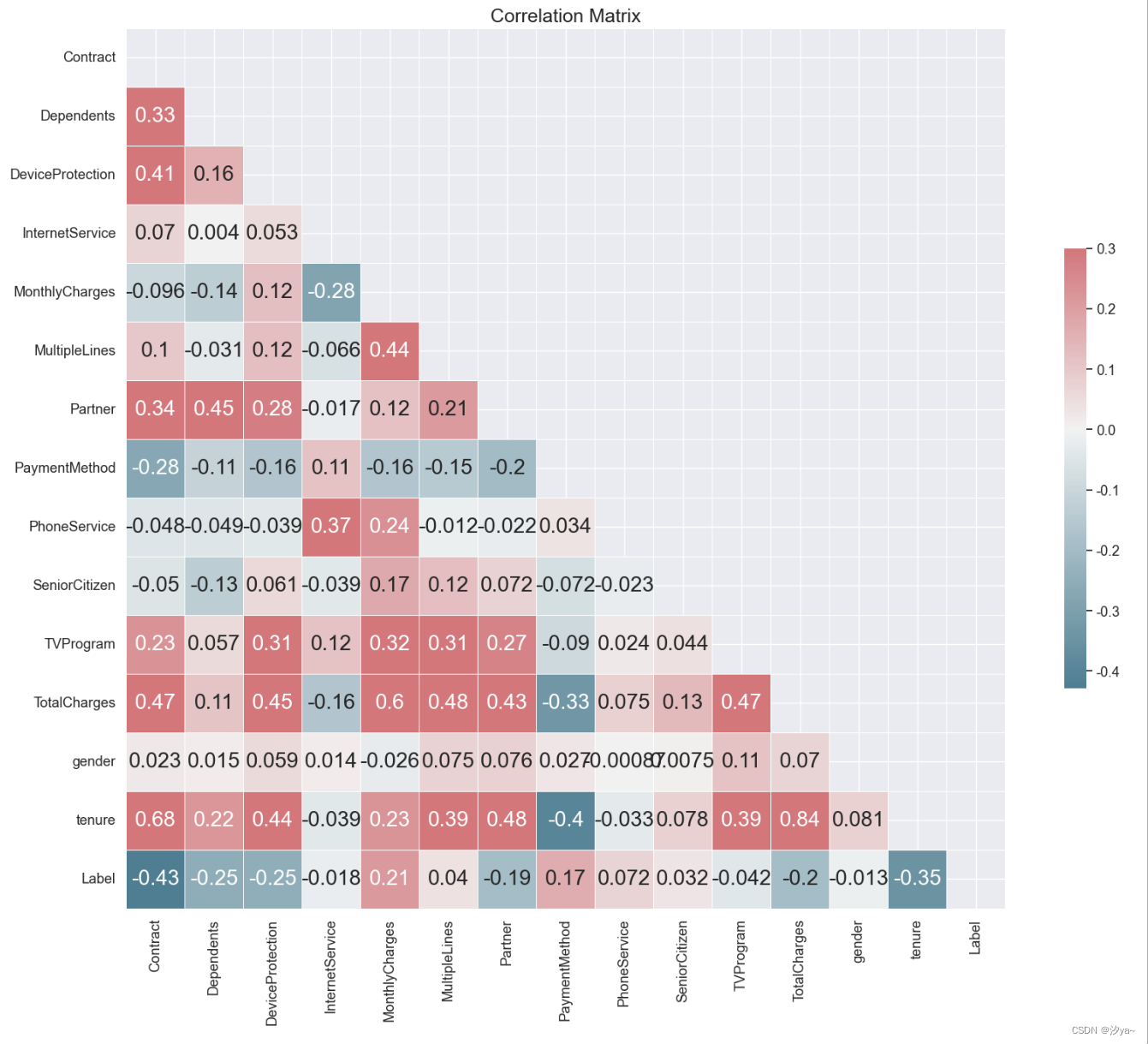
特征相关性分析

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

# 生成关联矩阵，排除 "ID" 列
corr = train.corr()

# 创建掩码矩阵
mask = np.triu(np.ones_like(corr, dtype=bool))

# 创建图表
f, ax = plt.subplots(figsize=(20, 15))

# 选择调色板
cmap = sns.diverging_palette(220, 10, as_cmap=True)

# 绘制热力图（半三角）
plt.title('Correlation Matrix', fontsize=18)
sns.heatmap(corr, mask=mask, cmap=cmap, vmax=.3, center=0, square=True, linewidths=.5, cbar_kws={"shrink": .5}, annot=True)

plt.show()

数据预处理

类别编码转换

from sklearn.preprocessing import LabelEncoder

columns_to_encode = ['Contract', 'Dependents', 'DeviceProtection', 'InternetService', 'MultipleLines', 'Partner', 'PaymentMethod', 'PhoneService', 'TVProgram', 'gender']

for column in columns_to_encode:
    label_encoder = LabelEncoder()
    # 合并训练集和测试集的数据进行拟合
    combined_data = pd.concat([train[column], test[column]])
    label_encoder.fit(combined_data)
    
    # 对训练集进行映射
    train[column] = label_encoder.transform(train[column])
    test[column] = label_encoder.transform(test[column])
   
# 初始化LabelEncoder并对训练集中的标签列进行映射
label_encoder = LabelEncoder()
train['Label'] = label_encoder.fit_transform(train['Label'])

train.head()

划分训练数据与测试数据

train.drop('ID', axis=1, inplace=True)
test.drop('ID', axis=1, inplace=True)

# 提取特征数据与目标数据
train_noLabel = train.iloc[:, :-1]  # 选择除最后一列外的所有列作为特征
y= train['Label']  # 标签列

# 把train数据划分成80％训练数据跟20%测试数据
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test = train_test_split(train_noLabel,y,test_size=0.2)
print("x_train shape:", x_train.shape, "x_test shape:", x_test.shape, "y_train shape:", y_train.shape, "y_test shape:", y_test.shape)

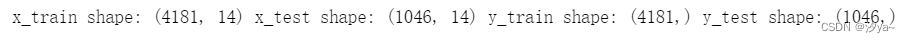
归一化处理

from sklearn.preprocessing import MinMaxScaler

# 需要归一化的列
columns_to_normalize = ['MonthlyCharges', 'TotalCharges', 'tenure']

# 初始化MinMaxScaler
scaler = MinMaxScaler()

# 对训练集中的指定列进行归一化
x_train[columns_to_normalize] = scaler.fit_transform(x_train[columns_to_normalize])

# 对测试集中的相同列进行归一化
x_test[columns_to_normalize] = scaler.transform(x_test[columns_to_normalize])
test[columns_to_normalize] = scaler.transform(test[columns_to_normalize])

模型建立