25考研数据结构复习·2.线性表.2

发布时间：2024年01月15日

  • 存储/物理结构

    • 顺序表（顺序存储）

      • 定义（如何用代码实现）

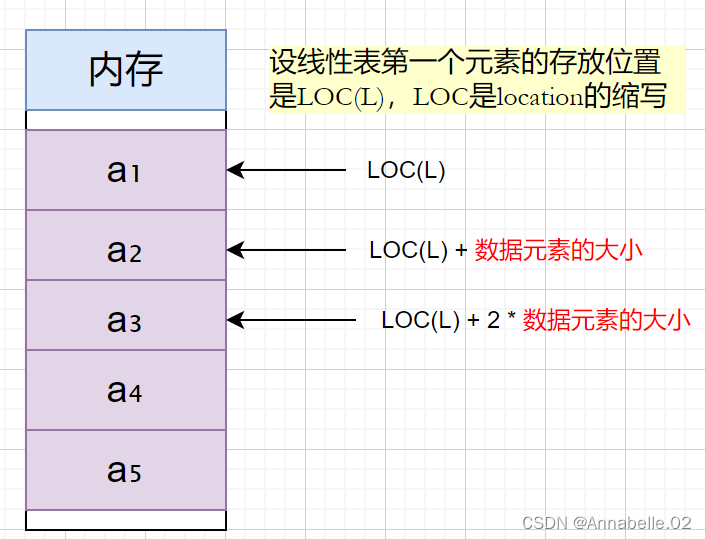
        顺序表——用顺序存储的方式实现线性表顺序存储。

        把逻辑上相邻的元素存储在物理位置上也相邻的存储单元中，元素之间的关系由存储单元的邻接关系来体现。

?

如何知道一个数据元素大小？

  • C语言 sizeof(ElemType)

    sizeof(int) = 4B

    typedef struct{
		int num;  //号数
		int people; //人数
}Customer;

    sizeof(Customer) = 8B

  • 基本操作的实现

    • 静态分配

      #define MaxSize 10  //定义最大长度
typedef struct{
		ElemType data[MaxSize];  //用静态的“数组”存放数据元素
		int length;  //顺序表的当前长度
}SqList;  //顺序表的类型定义（静态分配方式）Sq:sequence ——顺序，序列

      ? 
      #include <studio.h>
#define MaxSize 10  //定义最大长度
typedef struct{
		ElemType data[MaxSize];  //用静态的“数组”存放数据元素
		int length;  //顺序表的当前长度
}SqList;   //顺序表的类型定义

//基本操作——初始化一个顺序表
void InitList(SqList &L){
②		for(int i = 0;i < MaxSize;i++){
				L.data[i] = 0;  //将所有数据元素设置为默认初始值
③			L.length = 0;  //顺序表初始长度为0
		}
}
int main(){
①		SqList L;  //声明一个顺序表
		InitList(L);  //初始化顺序表
		//...未完待续，后续操作
		return 0;
}

      ?如果不给data数组设置默认初始值，会发生什么情况？

      #include <studio.h>
#define MaxSize 10  //定义最大长度
typedef struct{
		ElemType data[MaxSize];  //用静态的“数组”存放数据元素
		int length;  //顺序表的当前长度
}SqList;   //顺序表的类型定义

//基本操作——初始化一个顺序表
void InitList(SqList &L){
③			L.length = 0;  //顺序表初始长度为0
}
int main(){
①		SqList L;  //声明一个顺序表
		InitList(L);  //初始化顺序表
		//尝试“违规”打印整个data数组
		for(int i = 0; i < MaxSize; i++)
				printf("data[%d] = %d\\n",i,L.data[i]);
		return 0;
}

    • 内存中会有遗留的“脏数据”

      ?如果“数组”存满了怎么办？

      · 可以放弃治疗，顺序表的表厂刚开始确定后就无法更改（存储空间是静态的）

  • 动态分配

    #define InitSize 10  //顺序表的初始长度
typedef struct{
		ElemType * data;  //指示动态分配数组的指针
		int MaxSize;  //顺序表的最大容量
		int length;  //顺序表的当前长度
}SeqList;  //顺序表的类型定义（动态分配方式）

    💡 Key: 动态申请和释放内存空间

    C —— malloc、free函数

    • malloc函数

      L.data = (ElemType *) malloc (sizeof(ElemType) * InitSize);

      • 会申请一整片连续的存储空间，结束后return起始内存地址
      • (ElemType *) ：malloc函数返回一个指针，需要强制转型为你定义的数据元素类型指针
      • InitSize : malloc函数的参数，指明要分配多大的连续内存空间

    C++ ——new、delete关键字

#include <stdlib.h>  //malloc、free函数的头文件
#define InitSize 10  //默认的最大长度
typedef struct{
		ElemType * data;  //指示动态分配数组的指针
		int MaxSize;  //顺序表的最大容量
		int length;  //顺序表的当前长度
}SeqList; 

void InitList(SeqList &L){
		//用 malloc 函数申请一片连续的内存空间
		L.data = (int *)malloc(InitSize*sizeof(int));
		L.length = 0;
		L.MaxSize = InitSize;
} 

//增加动态数组的长度
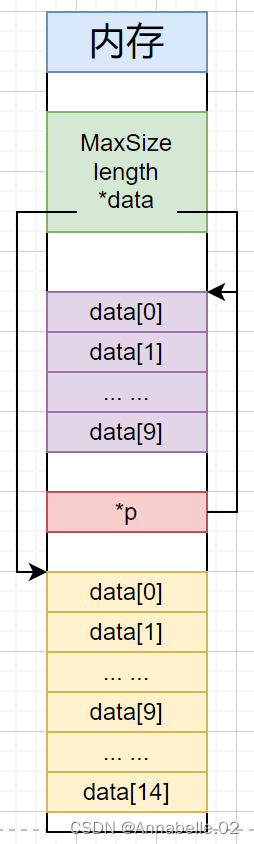
void IncreaseSize(SeqList &L,int len){
		int *p = L.data;
		L.data = (int *)malloc((L.MaxSize + len)*sizeof(int));
		for(int i = 0;i < L.length; i++){
				L.data[i] = p[i];  //将数据复制到新区域 
		}
		L.MaxSize = L.MaxSize + len;  //顺序表最大长度增加 len
		free(p);
}

int main(){
		SeqList L;  //声明一个顺序表
		InitList(L);  //初始化顺序表
		//...往顺序表中随便插入几个元素...
		IncreaseSize(L,5);
		return 0;
}

?

  • //将数据复制到新区域 → 时间开销大

  • 顺序表的特点

    • 随机访问，即可以在O(1)时间内找到第i个元素。

      代码实现：data[i -1]; 静态分配、动态分配都一样

    • 存储密度高，每个节点只存储数据元素

    • 拓展容量不方便（即便采用动态分配的方式实现，拓展长度的时间复杂度也比较高）

    • 插入、删除操作不方便，需要移动大量元素

?

写在前面：

线性表中位序从1开始；数组下标从0开始。?

  • 插入和删除

    • 插入

      ListInsert(&L,i,e): 插入操作。在表L中的第i个位置上插入指定元素e。

      用存储位置的相邻来体现数据元素之间的逻辑关系。

      • 代码实现
        #define InitSize 10  //定义最大长度
typedef struct
		int data[MaxSize];  //用静态的“数组”存放数据元素
		int length;  //顺序表的当前长度
}SeqList;   //顺序表的类型定义

//给定五个数字 length = 5
void ListInsert(SeqList &L,int i,int e){  //基本操作：在L的位序i处插入元素e
		for(int j = L.length;j >= i; j--)  //将第i个元素及之后的元素后移
				L.data[j] = L.data[j-1];  //注意位序、数组下标的关系，并从后面的元素依次移动
		L.data[i - 1] = e;  //在位置i处放入e
		L.length++;  //长度加1
} 

int main(){
		SeqList L;  //声明一个顺序表
		InitList(L);  //初始化顺序表
		//...往顺序表中随便插入几个元素...
		IncreaseSize(L,3,3);  //在第3个位置插入3
		return 0;
}

        ?如果最后是IncreaseSize(L,9,3);会发现3这个数据最后被插入在data[8]的位置上，但前两个位置上是空的。

        解决办法：加入一个条件判断，判断i的值是否合法。i的合法值[1,length + 1]

        //优化
#define InitSize 10  //定义最大长度
typedef struct
		int data[MaxSize];  //用静态的“数组”存放数据元素
		int length;  //顺序表的当前长度
}SeqList;   //顺序表的类型定义

bool ListInsert(SqList &L,int i,int e){
		if(i < 1 || i > L.length + 1)  //判断i的范围是否有效
				return false;
		if(L.length >= MaxSize)  //当前存储空间已满，不能插入
				return false;
		for(int j = L.length;j >= i;j--)  //将第i个元素及之后的元素后移
				L.data[j] = L.data[j - 1];
		L.data[i =-1] = e;  //在位置i处放入e
		L.length++;  //长度加1
		return true;
}

        · 好的算法，应该具有“健壮性”。能处理异常情况，并给使用者反馈。

      • 时间复杂度分析
        bool ListInsert(SqList &L,int i,int e){
		if(i < 1 || i > L.length + 1)  //判断i的范围是否有效
				return false;
		if(L.length >= MaxSize)  //当前存储空间已满，不能插入
				return false;
		for(int j = L.length;j >= i;j--)  //将第i个元素及之后的元素后移
				L.data[j] = L.data[j - 1];
		L.data[i =-1] = e;  //在位置i处放入e
		L.length++;  //长度加1
		return true;
}

        L.data[j] = L.data[j - 1]; —关注最深层循环语句的执行次数与问题规模n的关系

        问题规模 n = L.length（表长）

        • 最好情况：

        • 新元素插入到表尾，不需要移动元素

          i = n + 1,循环0次；最好时间复杂度 = O(1)

        • 最坏情况：

        • 新元素插入到表头，需要将原有的n个元素全都向后移动

          i = 1，循环n次；最坏时间复杂度 = O(n)

        • 平均情况：

        • 假设新元素插入到任何一个位置的概率相同

          即i = 1,2,3,…,length + 1的概率都是p = 1/n + 1

          i = 1，循环n次；i = 2时，循环n - 1次；i = 3时，循环n - 2次… … i = n + 1时，循环0次

?

平均时间复杂度 = O(n)?

  • 删除

    ListDelet(&L,i,&e)：删除操作。删除表L中第i个位置的元素，并用e返回删除元素的值

    • 代码实现
      bool ListInsert(SqList &L,int i,int &e){
		if(i < 1 || i > L.length)  //判断i的范围是否有效
				return false;
		e = L.data[i - 1];  //将被删除的元素赋值给e
		for(int j = i;j < L.length;j++)  //将第i个元素后哦的元素前移
				L.data[j - 1] = L.data[j];  //注意位序、数组下标的关系，并从前面的元素依次移动
		L.data[i =-1] = e;  
		L.length--;  //长度减1
		return true;
}

int main(){
		SeqList L;  //声明一个顺序表
		InitList(L);  //初始化顺序表
		//...往顺序表中随便插入几个元素...
		int e = -1;  //用变量e把删除的元素“带回来”
		if (ListDelete(L,3,e))
				printf("已经删除第3个元素，删除元素值为=%d\\n",e)
		else
				printf("位序i不合法，删除失败\\n")
		return 0;
}

      ?如果参数没有加引用符号，会怎样？

      加&，前面删除的元素赋值给e时，此时的e和main()中的e是一个。只是将前面e的值复制给了e = -1

  • 时间复杂度分析
    bool ListInsert(SqList &L,int i,int &e){
		if(i < 1 || i > L.length)  //判断i的范围是否有效
				return false;
		e = L.data[i - 1];  //将被删除的元素赋值给e
		for(int j = i;j < L.length;j++)  //将第i个元素后哦的元素前移
				L.data[j - 1] = L.data[j];  //注意位序、数组下标的关系，并从前面的元素依次移动
		L.data[i =-1] = e;  
		L.length--;  //长度减1
		return true;
}

    L.data[j - 1] = L.data[j]; —关注最深层循环语句的执行次数与问题规模n的关系

    问题规模 n = L.length（表长）

    • 最好情况：

    • 删除表尾元素，不需要移动元素

      i = n，循环0次；最好时间复杂度 = O(1)

    • 最坏情况：

    • 删除表头元素，需要将后续的n - 1个元素全都向前移动

      i = 1，循环n - 1次；最坏时间复杂度 = O(n)

    • 平均情况：

    • 假设删除任何一个元素的概率相同

      即i = 1,2,3,…,length的概率都是p = 1/n

      i = 1，循环n -1次；i = 2时，循环n - 2次；i = 3时，循环n -3次… … i = n时，循环0次

?

平均时间复杂度 = O(n)?

?

  • 按位查找和按值查找

    • 按位查找

      GetElem(L,i)：按位查找操作。获取表L中第i个位置的元素的值。

      • 代码实现
        静态分配
        #define MaxSize 10  //定义最大长度
typedef struct{
		ElemType data[MaxSize];  //用静态的“数组”存放数据元素
		int length;  //顺序表的当前长度
}SqList;  //顺序表的类型定义（静态分配方式）

ElemType GetElem(SqList L,int i){
		return L.data[i-1];
}
        动态分配
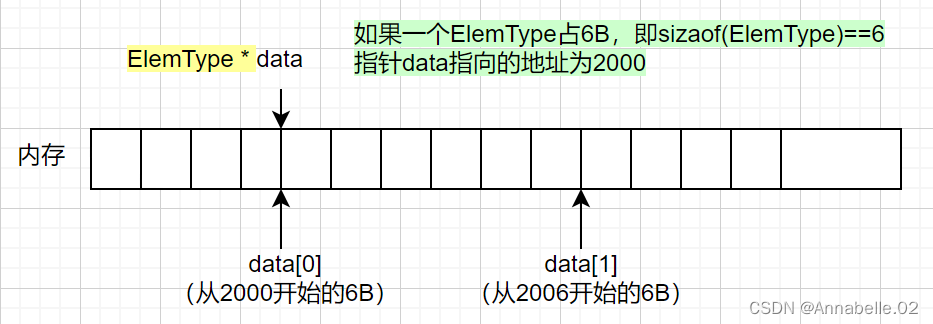
        #define InitSize 10  //顺序表的初始长度
typedef struct{
		ElemType * data;  //指示动态分配数组的指针 （这个data变量其实是一个指针）
		int MaxSize;  //顺序表的最大容量
		int length;  //顺序表的当前长度
}SeqList;  //顺序表的类型定义（动态分配方式）

ElemType GetElem(SqList L,int i){  //和访问普通数组的方法一样
		return L.data[i-1];
}

        用某个类型的指针和数组下标的方式来访问数据的话。那么，系统在背后取数据的时候每次取几个字节其实和指针指向的类型有关：

?

再次理解为什么malloc函数返回的存储空间起始地址要转换为与数据元素的数据类型相对应的指针?

  • 时间复杂度分析

    时间复杂度：O(1)

    💡“随机存取”特性

  • 按值查找

    LocateElem(L,e):按位查找操作。在表L中查找具有给定关键字值的元素。

    • 代码实现
      #define InitSize 10  //顺序表的初始长度
typedef struct{
		ElemType * data;  //指示动态分配数组的指针 
		int MaxSize;  //顺序表的最大容量
		int length;  //顺序表的当前长度
}SeqList;  //顺序表的类型定义（动态分配方式）

//在顺序表L中查找第一个元素值等于e的元素，并返回其位序
int LocateElem(SqlList L,ElemType e){
		for(int i = 0;i < L.length;i++)
				if(L.data[i] == e)
						return i + 1;  //数组下标为i的元素值等于e，返回其位序i + 1
		return 0;  //退出循环，说明查找失败
}

      具体例子：

      typedef struct{
		int * data;  //指示动态分配数组的指针 
		int MaxSize;  //顺序表的最大容量
		int length;  //顺序表的当前长度
}SeqList;  

//在顺序表L中查找第一个元素值等于e的元素，并返回其位序
int LocateElem(SqlList L,ElemType e){
		for(int i = 0;i < L.length;i++)
				if(L.data[i] == e)  //基本数据类型：int、char、double、float等可以直接用运算符“==”比较
						return i + 1;  
		return 0;  
}
//调用：LocalElem(L,9)

    • 💡结构类型的元素也这样吗？

      typedef struct{
		int num;  
		int people; 
}Customer;  

void test(){
		Customer a;
		a.num  = 1;
		a.people = 1;
		Customer b;
		b.num = 1;
		b.people = 1;
		if(a == b){
				printf("相等");//报错 Invalid operands to binary expression('Customer' and 'Customer')
		}else{
				printf("不相等");
		}
}

      💡注：C语言中，结构体的比较不能直接用“==”

      //优化
if (a.num == b.num && a.people ==b.people){
		printf("相等");
}else{
		printf("不相等");
}

      💡需要依次对比各个分量来判断两个结构体是否相等

      🗯?更好的办法：定义一个函数

  • 时间复杂度分析
    int LocateElem(SeqList L,ElemType e){
		for(int i = 0;i < L.lenghh;i++)
				if(L.data[i] == e)
						return i+1;  //数组下标为i的元素值等于e，返回其位序i + 1
		return 0;  //推出循环，说明查找失败
}

    if(L.data[i] == e) 关注最深层循环语句的执行次数与问题规模n的关系

    问题规模n = L.length（表长）

    • 最好情况：

    • 目标元素在表头

      循环1次；最好时间复杂度 = O(1)

    • 最坏情况：

    • 目标元素在表尾

      循环n 次；最坏时间复杂度 = O(n)

    • 平均情况：

    • 假设目标元素出现在任何一个位置的概率相同，都是1/n

      目标元素在第1位，循环1次；在第2位，循环2次，…，在第n位，循环n次

?

?

?

?

?

?

?

?

?

?

?

?

?

?

文章来源:https://blog.csdn.net/Annabelle___/article/details/135590365
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章