【深度学习】机器学习概述（一）机器学习三要素——模型、学习准则、优化算法

?

一、基本概念

??机器学习：通过算法使得机器能从大量数据中学习规律从而对新的样本做决策。

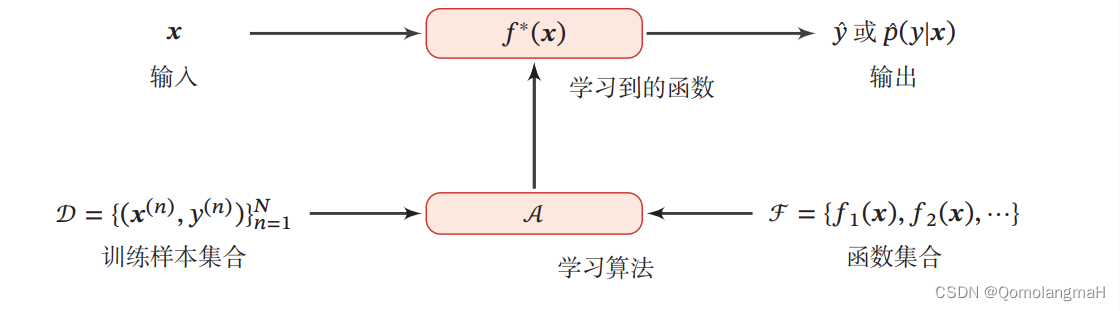
二、机器学习的三要素

??机器学习是从有限的观测数据中学习（或“猜测”）出具有一般性的规律，并可以将总结出来的规律推广应用到未观测样本上。
??机器学习方法可以粗略地分为三个基本要素：模型、学习准则、优化算法。

1. 模型

a. 线性模型

??线性模型是一类简单但广泛应用的模型，其假设空间为一个参数化的线性函数族。对于分类问题，一般使用广义线性函数，其表达式为：
$$f(\mathbf{x};\mathbf{\theta })={\mathbf{w}}^T\mathbf{x}+b$$

其中，参数 $\mathbf{\theta }$ 包含了权重向量 $\mathbf{w}$ 和偏置 $b$。在这个模型中，输入特征 $\mathbf{x}$ 和权重向量 $\mathbf{w}$ 的线性组合用于产生输出。这是一个简单而有效的模型，特别适用于问题的线性关系。

b. 非线性模型

??广义的非线性模型可以写为多个非线性基函数 $?(\mathbf{x})$ 的线性组合：$$f(\mathbf{x};\mathbf{\theta })={\mathbf{w}}^T?(\mathbf{x})+b$$其中，$?(\mathbf{x})=[{?}_1(\mathbf{x}),{?}_2(\mathbf{x}),\dots ,{?}_K(\mathbf{x}){]}^T$ 是由 $K$ 个非线性基函数组成的向量，参数 $\mathbf{\theta }$ 包含了权重向量 $\mathbf{w}$ 和偏置 $b$。

??如果 $?(\mathbf{x})$ 本身是可学习的基函数，例如：

$${?}_k(\mathbf{x})=h({\mathbf{w}}_k^T{?}^{\prime }(\mathbf{x})+b_k)$$其中，$h(?)$ 是非线性函数，${?}^{\prime }(\mathbf{x})$ 是另一组基函数，${\mathbf{w}}_k$ 和 $b_k$ 是可学习的参数，那么模型 $f(\mathbf{x};\mathbf{\theta })$ 就等价于神经网络模型。

??这种非线性模型通过引入非线性基函数 $?(\mathbf{x})$ 能够更灵活地适应数据中的复杂关系，使得模型能够捕捉到更丰富的特征信息。神经网络是非线性模型的一种重要实现方式。

2. 学习准则

a. 损失函数

1. 0-1损失函数

??0-1 损失函数是最直观的损失函数，用于衡量模型在训练集上的错误率。定义为：

$$\mathcal{L}(y,f(\mathbf{x};\mathbf{\theta }))=\{\begin{array}{ll}0& \text{if?}y=f(\mathbf{x};\mathbf{\theta })\\ 1& \text{if?}y\ne f(\mathbf{x};\mathbf{\theta })\end{array}$$

或者使用指示函数表示：

$$\mathcal{L}(y,f(\mathbf{x};\mathbf{\theta }))=\mathbb{I}(y\ne f(\mathbf{x};\mathbf{\theta }))$$

其中，$\mathbb{I}(?)$ 是指示函数。

??尽管0-1损失函数直观，但由于其非连续性和不可导性，通常用其他连续可导的损失函数替代。

2. 平方损失函数（回归问题）

??平方损失函数常用于回归问题，定义为：
$$\mathcal{L}(y,f(\mathbf{x};\mathbf{\theta }))=\frac{1}{2}(y?f(\mathbf{x};\mathbf{\theta }){)}^2$$

平方损失函数适用于预测标签为实数值的任务，但一般不适用于分类问题。

3. 交叉熵损失函数（Cross-Entropy Loss）

??可用于分类任务，用于衡量两个概率分布之间的差异

交叉熵损失函数常用于分类问题。假设样本的标签 $y$ 为离散的类别，模型的输出为类别标签的条件概率分布：
$$p(y=c|\mathbf{x};\mathbf{\theta })=f_c(\mathbf{x};\mathbf{\theta })$$

其中，$f_c(\mathbf{x};\mathbf{\theta })$ 表示模型输出向量的第 $c$ 维。交叉熵损失函数定义为：

$$\mathcal{L}(\mathbf{y},f(\mathbf{x};\mathbf{\theta }))=?\sum _{c=1}^C{y}_c\log f_c(\mathbf{x};\mathbf{\theta })$$

其中，$\mathbf{y}$ 是样本的真实标签向量，表示类别 $y$ 的one-hot向量。

4. Hinge 损失函数

??Hinge损失函数通常用于支持向量机等二分类问题，定义为：

$$\mathcal{L}(y,f(\mathbf{x};\mathbf{\theta }))=\max (0,1?yf(\mathbf{x};\mathbf{\theta }))$$

或使用ReLU函数表示：

$$\mathcal{L}(y,f(\mathbf{x};\mathbf{\theta }))=[1?yf(\mathbf{x};\mathbf{\theta }){]}_{+}$$

其中，$[x{]}_{+}=\max (0,x)$。

??这些损失函数在不同的任务和模型中发挥着关键的作用，选择合适的损失函数是模型设计中的重要决策。

b. 风险最小化准则

??在机器学习中，风险最小化准则是为了找到一个模型，使其在未知数据上的期望错误最小。然而，由于我们无法直接计算期望风险，通常使用经验风险（在训练集上的平均损失）来代替。以下是相关概念：

1. 经验风险最小化

??经验风险（Empirical Risk）是模型在训练集上的平均损失，表示为：

$${\mathcal{R}}_{\text{emp}}(\mathbf{\theta })=\frac{1}{N}\sum _{n=1}^N\mathcal{L}(y^{(n)},f({\mathbf{x}}^{(n)};\mathbf{\theta }))$$

其中，$\mathcal{L}$ 是损失函数，$N$ 是训练集中样本的数量。经验风险最小化准则的目标是找到一组参数 ${\mathbf{\theta }}^{?}$ 使经验风险最小化：

$${\mathbf{\theta }}^{?}=\arg \underset{\mathbf{\theta }}{\min }{\mathcal{R}}_{\text{emp}}(\mathbf{\theta })$$

这被称为经验风险最小化（Empirical Risk Minimization，ERM）准则。

2. 过拟合问题

??由于训练集通常是有限的，并且可能包含噪声，直接最小化经验风险可能导致模型在训练集上表现很好，但在未知数据上表现很差，即发生过拟合。

3. 结构风险最小化

??为了防止过拟合，可以在经验风险最小化的基础上引入正则化项，得到结构风险最小化（Structure Risk Minimization，SRM）准则：

$${\mathbf{\theta }}^{?}=\arg \underset{\mathbf{\theta }}{\min }\left({\mathcal{R}}_{\text{emp}}(\mathbf{\theta })+\frac{\lambda }{2}\Vert \mathbf{\theta }{\Vert }_2^2\right)$$

其中，$\lambda$ 是正则化参数，控制正则化的强度。正则化项 $\frac{\lambda }{2}\Vert \mathbf{\theta }{\Vert }_2^2$ 通过限制参数的大小，有助于防止过拟合。

4. 正则化项的选择

??正则化项可以使用不同的函数，例如 ${?}_1$ 范数。正则化的引入通常可以被解释为引入了参数的先验分布，使其不完全依赖于训练数据，从而有助于泛化。正则化的选择需要在模型训练中进行调整，以平衡经验风险和正则化项之间的权衡。

5. 欠拟合

??相反的情况是欠拟合（Underfitting），它发生在模型能力不足，不能很好地拟合训练数据，导致在训练集上的错误率较高。

??机器学习的目标不仅仅是在训练集上获得好的拟合，还需要在未知数据上表现良好，即具有较低的泛化错误。因此，学习准则的选择应该考虑到模型的泛化能力，防止过拟合和欠拟合的发生。

3. 优化

机器学习问题转化成为一个最优化问题

??一旦确定了训练集 $\mathcal{D}$、假设空间 $\mathcal{F}$ 以及学习准则，接下来的任务就是通过优化算法找到最优的模型 $f(\mathbf{x},{\mathbf{\theta }}^{?})$。机器学习的训练过程本质上是最优化问题的求解过程。

a. 参数与超参数

??优化可以分为参数优化和超参数优化两个方面：

1. 参数优化： $(\mathbf{x};\mathbf{\theta })$ 中的 $\mathbf{\theta }$ 称为模型的参数，这些参数通过优化算法进行学习。这些参数可以通过梯度下降等算法迭代地更新，以使损失函数最小化。

2. 超参数优化： 除了可学习的参数 $\mathbf{\theta }$ 外，还有一类参数用于定义模型结构或优化策略，这些参数被称为超参数。例如，聚类算法中的类别个数、梯度下降法中的学习率、正则化项的系数、神经网络的层数、支持向量机中的核函数等都是超参数。与可学习的参数不同，超参数的选取通常是一个组合优化问题，很难通过优化算法自动学习。通常，超参数的设定是基于经验或者通过搜索的方法对一组超参数组合进行不断试错调整。

b. 优化算法

??在训练模型的过程中，常用的优化算法包括梯度下降法、随机梯度下降法、牛顿法等。这些算法的核心思想是通过迭代更新模型的参数，使损失函数逐渐减小。

1. 梯度下降法（Gradient Descent）： 基本思想是沿着损失函数的梯度方向调整参数，以减小损失。学习率是一个重要的超参数，控制了每次迭代中参数更新的步长。

2. 随机梯度下降法（Stochastic Gradient Descent，SGD）： 与梯度下降法类似，但每次迭代只随机选择一个样本进行参数更新，通常更适用于大规模数据集。

3. 牛顿法（Newton’s Method）： 利用损失函数的二阶导数信息进行参数更新，收敛速度通常比梯度下降法快，但计算代价较高。

4. 共轭梯度法（Conjugate Gradient）： 特别适用于解线性方程组问题。

5. 拟牛顿法（Quasi-Newton）： 通过近似 Hessian 矩阵来加速梯度下降法的收敛速度。

6. Adam、Adagrad、RMSprop 等自适应学习率算法： 这些算法通过自适应地调整学习率，使得不同参数可以有不同的学习速度。

??选择合适的优化算法以及超参数是训练过程中的关键问题，通常需要进行实验和调参来获得最佳性能。

机器学习 = 优化？

??机器学习并不是只是单纯追求最小化经验风险