Paper Reading [Motion Planning]——Robot Motion Generation

综述阅读

CuRobo: Parallelized Collision-Free Robot Motion Generation.

CuRobo: CUDA加速的机器人库。并行化的无碰撞机器人运动生成。

本文将机械臂的无碰撞运动生成问题[collision-free motion generation]表述为全局运动优化问题[global motion optimization problem]。开发了一种并行优化技术，在大规模并行GPU上证明了该技术的有效性。

将简单的优化技术与许多并行种子parallel seeds相结合，可以在平均53ms的时间内解决一些困难的运动生成问题，比SOTA轨迹优化方法快62倍。

将L-BFGS(用于非线性优化问题的迭代数值优化算法) step direction estimation 与一种新颖的 parallel noisy line search scheme and a particle-based optimization solver 相结合.

本文设计了：

1. 一种并行几何规划器[parallel geometric planner]，比SOTA RRTConnect的实现至少快28倍。
2. 一种无碰撞IK 求解器[collision-free IK solver]，每秒解决超过9000次查询。
3. 准备发布GPU 加速库CuRobo，其中包含用于机器人运动生成的核心组件。

Introduction

该领域长期以来一直在进行问题拆解，形成了一些标准方法。这些方法通常首先规划无碰撞的几何路径，然后平滑这些路径以提高动态效率。

但是，对于优化optimization和规划planning之间相互联系的研究越来越多的表明，优化是一种强大的工具，远远超出了轨迹平滑的范畴，仅轨迹优化就有广泛的应用。

1、

Robot navigation problem is a large global motion optimization problem.

• global minimum ??
• high-performing local minima ??

许多策略遵循选择许多种子候选并对每个种子执行局部优化的简单模式。

2、

传统CPU-based design运算效率低。主要是由于pipelined systems

• a motion planner -> out: a single best candidate seed
• -> pass: -> an optimizer -> out: a single local optimization.

利用并行处理来加速运动规划和优化。

3、

现有的算法原理：

• heuristic initialization
• restarts with randomized noise of the initial seed

Main contributions:

• Parallel Optimization — 并行优化器

  a GPU batched L-BFGS optimizer.

  use an approximate parallel line search scheme & a particle-based optimizer

• Parallel Geometric Planner — 并行几何规划器

• Performant Kinematics and Signed Distance Kernels

  设计高性能CUDA内核用于机器人运动学和有符号距离计算，比传统基于CPU的方法快了10,000倍

• Validation on a Low-Power Device

• Library

  开发CuRobo.

MOTION GENERATION AS OPTIMIZATION

$$start:{\theta }_0\to final:{\theta }_T$$

在这种状态下，task cost $ C(\theta_{T})$低于期望阈值。同时，这个过程中还要满足系统约束。

具体来说，我们想要得到一个满足机器人关节限制(position, velocity, acceleration)，不与自身或者环境发生碰撞，且在最后一个时间步$T$达到目标位姿$X_g$的joint-space trajectory ${\theta }_{[0,T]}$.

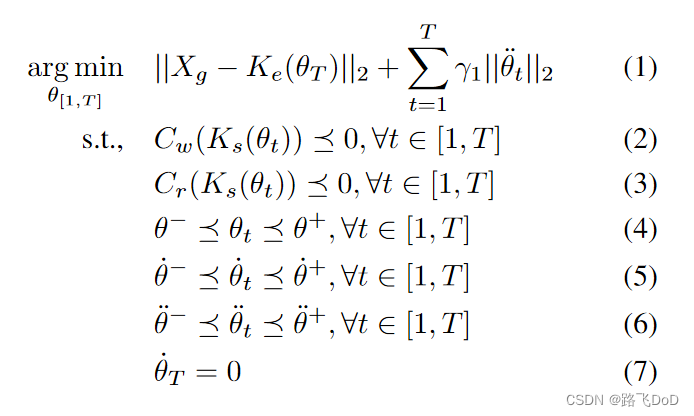
$Ke(?)$：给定关节构型$\theta$的情况下计算末端执行器位姿的运动学函数。

$Ks(?)$：计算填充机器人体积的球体的位置。这些球体用于检查与世界$C_w$和机器人本身$C_r$的碰撞。($C_w,C_r$)返回与最近障碍物的距离。

在达到目标位姿Xg的问题设置中，终端状态优化问题可以归结为一个包含如下约束的无碰撞逆运动学(IK)问题：

1. 包含位姿代价 Eq.1 left
2. 碰撞约束 Eq.2-Eq.3
3. 关节极限约束 Eq.4
   

To solve the optimization problem:

• sampling-based optimization
• gradient-based optimization

许多轨迹优化方法将硬约束近似为软约束，将其视为具有大权重的成本项，以将优化问题从具有非凸约束[nonconvex constraints]的问题转化为一个带有箱式约束的非凸[a box-constrained nonconvex]优化问题。(每个变量的取值范围被限定在一个特定的区间, 约束在每个维度上都是线性的)

We implement a Quasi-Newton solver.（步长的估计是通过L-BFGS算法中的拟牛顿方法来实现的，其中使用了限制内存来存储先前迭代步骤的信息。）

Gauss-Newton Solvers也很普遍和重要，这里作者挖了个坑。

CabiNet: Scaling Neural Collision Detection for Object Rearrangement with Procedural Scene Generation.

CabiNet

CabiNet: 扩展神经碰撞检测以进行物体重新排列及过程化场景生成.

CabiNet能够在新颖的、杂乱的环境中处理复杂的重排列的任务，仅仅依赖部分点云观测图像，而不需要物体或场景内的建模。

本模型通过单目深度相机获得物体和场景的点云图像，预测场景中collisions of SE(3) object poses.

Collision Detection from Point Clouds

1. computational geometry libraries (object mesh is known).
2. voxelize or spherize. 对点云进行体素化或者球化处理，将碰撞检测问题表述为评估任何元素是否与机器人链接发生碰撞。

SceneCollisionNet将碰撞检测问题框架化为传统体素方法和数据驱动方法的混合体。它将场景编码为粗糙的体素，其中每个体素由深度嵌入向量表示。每个碰撞查询被定义为查询对象和场景点云的一对。碰撞检测通过二元分类器进行，该分类器以场景体素嵌入、对象嵌入和相对SE(3)变换为输入。

首先使用体素化和3D卷积对场景点云进行编码，捕获场景特征。然后使用object encoder对物体点云进行编码，提取对象特征。然后，使用场景特征与对象特征一起预测场景-对象碰撞查询。

我们还在潜在向量z和当前夹爪位置（绿色显示）的条件下预测重新排列的路径点（蓝色显示）。

Learning to Optimize in Model Predictive Control

Byron Boots - University of Washington

很多工作集中在利用机器学习来改善MPC的性能，通常是通过学习或微调动态或成本函数。与之相反，我们关注于学习如何对其进行更有效的优化。换句话说，改善MPC中的更新规则。这在基于采样的MPC中的尤其有用，因为通常我们是出于计算方面考量，希望最小化样本数量。但与此同时，计算效率的代价是性能降低。

通过动态镜像下降(Dynamic Mirror Descent DMD, a first-order online learning algorithm)的通用框架，可以统一许多流行的MPC算法。

最近的研究探讨了学习优化，其中更新规则由**函数逼近器（如神经网络）**指定，可以通过经验提高优化性能。

这与大多数现有基于学习的MPC方法形成对比，后者要么专注于学习一个良好的动力学模型，在目标函数中引入学到的成本形状术语以及将MPC与学到的值函数耦合，要么学习一个良好的MPC的热启动（更接近最优解的初始点，从而加速优化算法的收敛过程）以进行细化。

To be continue……